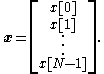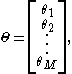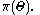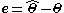Estimation theory
Encyclopedia
Estimation theory is a branch of statistics
and signal processing
that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An estimator
attempts to approximate the unknown parameters using the measurements.
For example, it is desired to estimate the proportion of a population of voters who will vote for a particular candidate. That proportion is the unobservable parameter; the estimate is based on a small random sample of voters.
Or, for example, in radar
the goal is to estimate the range of objects (airplanes, boats, etc.) by analyzing the two-way transit timing of received echoes of transmitted pulses. Since the reflected pulses are unavoidably embedded in electrical noise, their measured values are randomly distributed, so that the transit time must be estimated.
In estimation theory, it is assumed the measured data is random with probability distribution dependent on the parameters of interest. For example, in electrical communication theory, the measurements which contain information regarding the parameters of interest are often associated with a noisy signal
. Without randomness, or noise, the problem would be deterministic
and estimation would not be needed.
The estimator takes the measured data as input and produces an estimate of the parameters.
It is also preferable to derive an estimator that exhibits optimality
. Estimator optimality usually refers to achieving minimum average error over some class of estimators, for example, a minimum variance unbiased estimator. In this case, the class is the set of unbiased estimators, and the average error measure is variance (average squared error between the value of the estimate and the parameter). However, optimal estimators do not always exist.
These are the general steps to arrive at an estimator:
After arriving at an estimator, real data might show that the model used to derive the estimator is incorrect, which may require repeating these steps to find a new estimator.
A non-implementable or infeasible estimator may need to be scrapped and the process started anew.
In summary, the estimator estimates the parameters of a physical model based on measured data.
These are needed to ensure the estimator has some mathematical tractability instead of being based on "good feel".
The first is a set of statistical samples taken from a random vector (RV) of size N. Put into a vector,
Secondly, we have the corresponding M parameters
which need to be established with their probability density function
(pdf) or probability mass function
(pmf)
It is also possible for the parameters themselves to have a probability distribution (e.g., Bayesian statistics
). It is then necessary to define the Bayesian probability
After the model is formed, the goal is to estimate the parameters, commonly denoted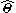
, where the "hat" indicates the estimate.
One common estimator is the minimum mean squared error estimator, which utilizes the error between the estimated parameters and the actual value of the parameters
as the basis for optimality. This error term is then squared and minimized for the MMSE estimator.
,
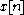, of 
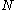independent
samples that consists of an unknown constant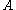
with additive white Gaussian noise
(AWGN)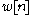
with known variance
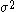(i.e., 
).
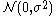Since the variance is known then the only unknown parameter is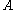
.
The model for the signal is then
Two possible (of many) estimators are:
Both of these estimators have a mean
of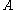
, which can be shown through taking the expected value
of each estimator
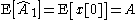
and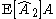
At this point, these two estimators would appear to perform the same.
However, the difference between them becomes apparent when comparing the variances.
and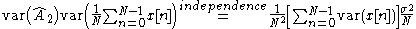
It would seem that the sample mean is a better estimator since, it's variance is lower for every N>1.
estimator, the probability density function
(pdf) of the noise for one sample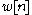
is
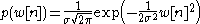
and the probability of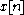
becomes (
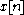can be thought of a 
)
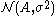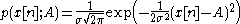
By independence, the probability of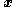
becomes
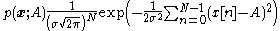
Taking the natural logarithm
of the pdf
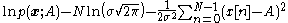
and the maximum likelihood estimator is
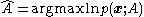
Taking the first derivative
of the log-likelihood function
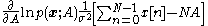
and setting it to zero
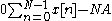
This results in the maximum likelihood estimator
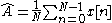
which is simply the sample mean.
From this example, it was found that the sample mean is the maximum likelihood estimator for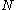
samples of a fixed, unknown parameter corrupted by AWGN.
number
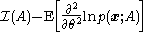
and copying from above
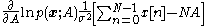
Taking the second derivative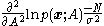
and finding the negative expected value is trivial since it is now a deterministic constant
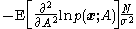
Finally, putting the Fisher information into
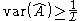
results in
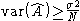
Comparing this to the variance of the sample mean (determined previously) shows that the sample mean is equal to the Cramér–Rao lower bound for all values of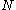
and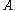 
.
In other words, the sample mean is the (necessarily unique) efficient estimator, and thus also the minimum variance unbiased estimator (MVUE), in addition to being the maximum likelihood
estimator.
estimators and likelihood functions.
Given a discrete uniform distribution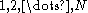
with unknown maximum, the UMVU estimator for the maximum is given by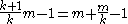
where m is the sample maximum and k is the sample size
, sampling without replacement. This problem is commonly known as the German tank problem
, due to application of maximum estimation to estimates of German tank production during World War II
.
The formula may be understood intuitively as:
the gap being added to compensate for the negative bias of the sample maximum as an estimator for the population maximum.The sample maximum is never more than the population maximum, but can be less, hence it is a biased estimator: it will tend to underestimate the population maximum.
This has a variance of
so a standard deviation of approximately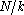
, the (population) average size of a gap between samples; compare 
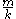above. This can be seen as a very simple case of maximum spacing estimation
.
The sample maximum is the maximum likelihood
estimator for the population maximum, but, as discussed above, it is biased.
Some of these fields include (but are by no means limited to):
Measured data are likely to be subject to noise or uncertainty and it is through statistical probability
that optimal
solutions are sought to extract as much information
from the data as possible.
:Category:Estimation for specific distributions
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
attempts to approximate the unknown parameters using the measurements.
For example, it is desired to estimate the proportion of a population of voters who will vote for a particular candidate. That proportion is the unobservable parameter; the estimate is based on a small random sample of voters.
Or, for example, in radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
the goal is to estimate the range of objects (airplanes, boats, etc.) by analyzing the two-way transit timing of received echoes of transmitted pulses. Since the reflected pulses are unavoidably embedded in electrical noise, their measured values are randomly distributed, so that the transit time must be estimated.
In estimation theory, it is assumed the measured data is random with probability distribution dependent on the parameters of interest. For example, in electrical communication theory, the measurements which contain information regarding the parameters of interest are often associated with a noisy signal
Signal (electrical engineering)
In the fields of communications, signal processing, and in electrical engineering more generally, a signal is any time-varying or spatial-varying quantity....
. Without randomness, or noise, the problem would be deterministic
Determinism
Determinism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
and estimation would not be needed.
Estimation process
The entire purpose of estimation theory is to arrive at an estimator, and preferably an implementable one that could actually be used.The estimator takes the measured data as input and produces an estimate of the parameters.
It is also preferable to derive an estimator that exhibits optimality
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
. Estimator optimality usually refers to achieving minimum average error over some class of estimators, for example, a minimum variance unbiased estimator. In this case, the class is the set of unbiased estimators, and the average error measure is variance (average squared error between the value of the estimate and the parameter). However, optimal estimators do not always exist.
These are the general steps to arrive at an estimator:
- In order to arrive at a desired estimator, it is first necessary to determine a probability distribution for the measured data, and the distribution's dependence on the unknown parameters of interest. Often, the probability distribution may be derived from physical models that explicitly show how the measured data depends on the parameters to be estimated, and how the data is corrupted by random errors or noise. In other cases, the probability distribution for the measured data is simply "assumed", for example, based on familiarity with the measured data and/or for analytical convenience.
- After deciding upon a probabilistic model, it is helpful to find the limitations placed upon an estimator. This limitation, for example, can be found through the Cramér–Rao bound.
- Next, an estimator needs to be developed or applied if an already known estimator is valid for the model. The estimator needs to be tested against the limitations to determine if it is an optimal estimator (if so, then no other estimator will perform better).
- Finally, experiments or simulations can be run using the estimator to test its performance.
After arriving at an estimator, real data might show that the model used to derive the estimator is incorrect, which may require repeating these steps to find a new estimator.
A non-implementable or infeasible estimator may need to be scrapped and the process started anew.
In summary, the estimator estimates the parameters of a physical model based on measured data.
Basics
To build a model, several statistical "ingredients" need to be known.These are needed to ensure the estimator has some mathematical tractability instead of being based on "good feel".
The first is a set of statistical samples taken from a random vector (RV) of size N. Put into a vector,
Secondly, we have the corresponding M parameters
which need to be established with their probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(pdf) or probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
(pmf)
It is also possible for the parameters themselves to have a probability distribution (e.g., Bayesian statistics
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
). It is then necessary to define the Bayesian probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
After the model is formed, the goal is to estimate the parameters, commonly denoted
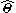, where the "hat" indicates the estimate.One common estimator is the minimum mean squared error estimator, which utilizes the error between the estimated parameters and the actual value of the parameters
as the basis for optimality. This error term is then squared and minimized for the MMSE estimator.
Estimators
Commonly-used estimators and estimation methods, and topics related to them:- Maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimators - Bayes estimatorBayes estimatorIn estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function . Equivalently, it maximizes the posterior expectation of a utility function...
s - Method of moments estimators
- Cramér–Rao bound
- Minimum mean squared error (MMSE), also known as Bayes least squared error (BLSE)
- Maximum a posterioriMaximum a posterioriIn Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
(MAP) - Minimum variance unbiased estimator (MVUE)
- Best linear unbiased estimator (BLUE)
- Unbiased estimators — see estimator bias.
- Particle filterParticle filterIn statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
- Markov chain Monte CarloMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
(MCMC) - Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
- Ensemble Kalman filterEnsemble Kalman filterThe ensemble Kalman filter is a recursive filter suitable for problems with a large number of variables, such as discretizations of partial differential equations in geophysical models...
(EnKF) - Wiener filterWiener filterIn signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
Unknown constant in additive white Gaussian noise
Consider a received discrete signalDiscrete signal
A discrete signal or discrete-time signal is a time series consisting of a sequence of qualities...
,
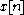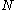, of independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
samples that consists of an unknown constant
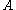with additive white Gaussian noiseAdditive white Gaussian noise
Additive white Gaussian noise is a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density and a Gaussian distribution of amplitude. The model does not account for fading, frequency selectivity, interference,...
(AWGN)
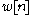with known varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
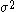(i.e., 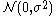).Since the variance is known then the only unknown parameter is
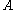.The model for the signal is then
Two possible (of many) estimators are:
-
-
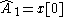
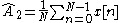which is the sample mean
Both of these estimators have a mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of
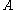, which can be shown through taking the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of each estimator
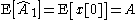
and
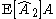
At this point, these two estimators would appear to perform the same.
However, the difference between them becomes apparent when comparing the variances.
and
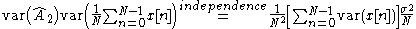
It would seem that the sample mean is a better estimator since, it's variance is lower for every N>1.
Maximum likelihood
Continuing the example using the maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator, the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(pdf) of the noise for one sample
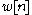is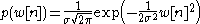and the probability of
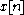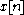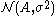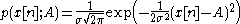
becomes ( can be thought of a )By independence, the probability of
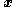becomes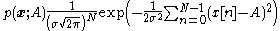Taking the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the pdf
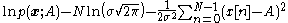
and the maximum likelihood estimator is
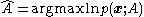
Taking the first derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the log-likelihood function
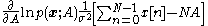
and setting it to zero
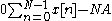
This results in the maximum likelihood estimator
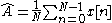
which is simply the sample mean.
From this example, it was found that the sample mean is the maximum likelihood estimator for
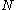samples of a fixed, unknown parameter corrupted by AWGN.Cramér–Rao lower bound
To find the Cramér–Rao lower bound (CRLB) of the sample mean estimator, it is first necessary to find the Fisher informationFisher information
In mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
number
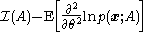
and copying from above
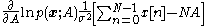
Taking the second derivative
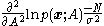
and finding the negative expected value is trivial since it is now a deterministic constant
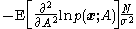
Finally, putting the Fisher information into
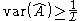
results in
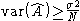
Comparing this to the variance of the sample mean (determined previously) shows that the sample mean is equal to the Cramér–Rao lower bound for all values of
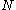and 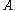.In other words, the sample mean is the (necessarily unique) efficient estimator, and thus also the minimum variance unbiased estimator (MVUE), in addition to being the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator.
Maximum of a uniform distribution
One of the simplest non-trivial examples of estimation is the estimation of the maximum of a uniform distribution. It is used as a hands-on classroom exercise and to illustrate basic principles of estimation theory. Further, in the case of estimation based on a single sample, it demonstrates philosophical issues and possible misunderstandings in the use of maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimators and likelihood functions.
Given a discrete uniform distribution
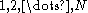with unknown maximum, the UMVU estimator for the maximum is given by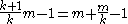where m is the sample maximum and k is the sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
, sampling without replacement. This problem is commonly known as the German tank problem
German tank problem
In the statistical theory of estimation, estimating the maximum of a uniform distribution is a common illustration of differences between estimation methods...
, due to application of maximum estimation to estimates of German tank production during World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
.
The formula may be understood intuitively as:
- "The sample maximum plus the average gap between observations in the sample",
the gap being added to compensate for the negative bias of the sample maximum as an estimator for the population maximum.The sample maximum is never more than the population maximum, but can be less, hence it is a biased estimator: it will tend to underestimate the population maximum.
This has a variance of
so a standard deviation of approximately
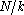, the (population) average size of a gap between samples; compare 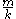above. This can be seen as a very simple case of maximum spacing estimationMaximum spacing estimation
In statistics, maximum spacing estimation , or maximum product of spacing estimation , is a method for estimating the parameters of a univariate statistical model...
.
The sample maximum is the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator for the population maximum, but, as discussed above, it is biased.
Applications
Numerous fields require the use of estimation theory.Some of these fields include (but are by no means limited to):
- Interpretation of scientific experimentExperimentAn experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
s - Signal processingSignal processingSignal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
- Clinical trialClinical trialClinical trials are a set of procedures in medical research and drug development that are conducted to allow safety and efficacy data to be collected for health interventions...
s - Opinion pollOpinion pollAn opinion poll, sometimes simply referred to as a poll is a survey of public opinion from a particular sample. Opinion polls are usually designed to represent the opinions of a population by conducting a series of questions and then extrapolating generalities in ratio or within confidence...
s - Quality controlQuality controlQuality control, or QC for short, is a process by which entities review the quality of all factors involved in production. This approach places an emphasis on three aspects:...
- TelecommunicationTelecommunicationTelecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
s - Project managementProject managementProject management is the discipline of planning, organizing, securing, and managing resources to achieve specific goals. A project is a temporary endeavor with a defined beginning and end , undertaken to meet unique goals and objectives, typically to bring about beneficial change or added value...
- Software engineeringSoftware engineeringSoftware Engineering is the application of a systematic, disciplined, quantifiable approach to the development, operation, and maintenance of software, and the study of these approaches; that is, the application of engineering to software...
- Control theoryControl theoryControl theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
(in particular Adaptive controlAdaptive controlAdaptive control is the control method used by a controller which must adapt to a controlled system with parameters which vary, or are initially uncertain. For example, as an aircraft flies, its mass will slowly decrease as a result of fuel consumption; a control law is needed that adapts itself...
) - Network intrusion detection systemNetwork intrusion detection systemA Network Intrusion Detection System is an intrusion detection system that tries to detect malicious activity such as denial of service attacks, port scans or even attempts to crack into computers by Network Security Monitoring of network traffic.A NIDS reads all the incoming packets and tries to...
- Orbit determinationOrbit determinationOrbit determination is a branch of astronomy specialised in calculating, and hence predicting, the orbits of objects such as moons, planets, and spacecraft . These orbits could be orbiting the Earth, or other bodies...
Measured data are likely to be subject to noise or uncertainty and it is through statistical probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that optimal
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
solutions are sought to extract as much information
Fisher information
In mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
from the data as possible.
See also
:Category:Estimation theory:Category:Estimation for specific distributions
- Best linear unbiased estimator (BLUE)
- Chebyshev centerChebyshev centerIn geometry, the Chebyshev center of a bounded set Q having non-empty interior is the center of the minimal-radius ball enclosing the entire set Q, or, alternatively, the center of largest inscribed ball of Q ....
- Completeness (statistics)Completeness (statistics)In statistics, completeness is a property of a statistic in relation to a model for a set of observed data. In essence, it is a condition which ensures that the parameters of the probability distribution representing the model can all be estimated on the basis of the statistic: it ensures that the...
- Cramér–Rao bound
- Detection theoryDetection theoryDetection theory, or signal detection theory, is a means to quantify the ability to discern between information-bearing energy patterns and random energy patterns that distract from the information Detection theory, or signal detection theory, is a means to quantify the ability to discern between...
- Efficiency (statistics)Efficiency (statistics)In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
- EstimatorEstimatorIn statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
, Estimator bias - Expectation-maximization algorithmExpectation-maximization algorithmIn statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
(EM algorithm) - Information theoryInformation theoryInformation theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
- Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
- Least-squares spectral analysisLeast-squares spectral analysisLeast-squares spectral analysis is a method of estimating a frequency spectrum, based on a least squares fit of sinusoids to data samples, similar to Fourier analysis...
- Markov chain Monte CarloMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
(MCMC) - Matched filterMatched filterIn telecommunications, a matched filter is obtained by correlating a known signal, or template, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template...
- Maximum a posterioriMaximum a posterioriIn Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
(MAP) - Maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
- Maximum entropy spectral estimationMaximum entropy spectral estimationThe maximum entropy method applied to spectral density estimation. The overall idea is that the maximum entropy rate stochastic process that satisfies the given constant autocorrelation and variance constraints, is a linear Gauss-Markov process with i.i.d...
- Method of moments, generalized method of momentsGeneralized method of momentsIn econometrics, generalized method of moments is a generic method for estimating parameters in statistical models. Usually it is applied in the context of semiparametric models, where the parameter of interest is finite-dimensional, whereas the full shape of the distribution function of the data...
- Minimum mean squared error (MMSE)
- Minimum variance unbiased estimator (MVUE)
- Nuisance parameter
- Parametric equationParametric equationIn mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
- Particle filterParticle filterIn statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
- Rao–Blackwell theoremRao–Blackwell theoremIn statistics, the Rao–Blackwell theorem, sometimes referred to as the Rao–Blackwell–Kolmogorov theorem, is a result which characterizes the transformation of an arbitrarily crude estimator into an estimator that is optimal by the mean-squared-error criterion or any of a variety of similar...
- Spectral densitySpectral densityIn statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
, Spectral density estimationSpectral density estimationIn statistical signal processing, the goal of spectral density estimation is to estimate the spectral density of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal... - Statistical signal processingStatistical signal processingStatistical signal processing is an area of Applied Mathematics and Signal Processing that treats signals as stochastic processes, dealing with their statistical properties...
- Sufficiency (statistics)Sufficiency (statistics)In statistics, a sufficient statistic is a statistic which has the property of sufficiency with respect to a statistical model and its associated unknown parameter, meaning that "no other statistic which can be calculated from the same sample provides any additional information as to the value of...
- Wiener filterWiener filterIn signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
Reference list
- Theory of Point Estimation by E.L. Lehmann and G. Casella. (ISBN-10: 0387985026)
- Systems Cost Engineering by Dale Shermon. (ISBN 978-0-566-08861-2)
- Mathematical Statistics and Data Analysis by John Rice. (ISBN 0-534-209343)
- Fundamentals of Statistical Signal Processing: Estimation Theory by Steven M. Kay (ISBN 0-13-345711-7)
- An Introduction to Signal Detection and Estimation by H. Vincent Poor (ISBN 0-387-94173-8)
- Detection, Estimation, and Modulation Theory, Part 1 by Harry L. Van Trees (ISBN 0-471-09517-6; website)
- Optimal State Estimation: Kalman, H-infinity, and Nonlinear Approaches by Dan Simon website
- Ali H. SayedAli H. SayedAli H. Sayed is Professor of Electrical Engineering at the University of California, Los Angeles , where he teaches and conducts research on Adaptation, Learning, Statistical Signal Processing, and Signal Processing for Communications. He is the Director of the UCLA Adaptive Systems Laboratory...
, Adaptive Filters, Wiley, NJ, 2008, ISBN 978-0-470-25388-5. - Ali H. SayedAli H. SayedAli H. Sayed is Professor of Electrical Engineering at the University of California, Los Angeles , where he teaches and conducts research on Adaptation, Learning, Statistical Signal Processing, and Signal Processing for Communications. He is the Director of the UCLA Adaptive Systems Laboratory...
, Fundamentals of Adaptive Filtering, Wiley, NJ, 2003, ISBN 0-471-46126-1. - Thomas KailathThomas KailathThomas Kailath is an Indian electrical engineer, information theorist, control engineer, entrepreneur and the Hitachi America Professor of Engineering, Emeritus, at Stanford University...
, Ali H. SayedAli H. SayedAli H. Sayed is Professor of Electrical Engineering at the University of California, Los Angeles , where he teaches and conducts research on Adaptation, Learning, Statistical Signal Processing, and Signal Processing for Communications. He is the Director of the UCLA Adaptive Systems Laboratory...
, and Babak HassibiBabak HassibiBabak Hassibi is an Iranian-American electrical engineer who is currently professor of Electrical Engineering and head of the Department of Electrical Engineering at the California Institute of Technology ....
, Linear Estimation, Prentice-Hall, NJ, 2000, ISBN 978-0-13-022464-4. - Babak HassibiBabak HassibiBabak Hassibi is an Iranian-American electrical engineer who is currently professor of Electrical Engineering and head of the Department of Electrical Engineering at the California Institute of Technology ....
, Ali H. SayedAli H. SayedAli H. Sayed is Professor of Electrical Engineering at the University of California, Los Angeles , where he teaches and conducts research on Adaptation, Learning, Statistical Signal Processing, and Signal Processing for Communications. He is the Director of the UCLA Adaptive Systems Laboratory...
, and Thomas KailathThomas KailathThomas Kailath is an Indian electrical engineer, information theorist, control engineer, entrepreneur and the Hitachi America Professor of Engineering, Emeritus, at Stanford University...
, Indefinite Quadratic Estimation and Control: A Unified Approach to H2 and Hoo Theories, Society for Industrial & Applied Mathematics (SIAM), PA, 1999, ISBN 978-0-89871-411-1. - V.G.Voinov, M.S.Nikulin, "Unbiased estimators and their applications. Vol.1: Univariate case", Kluwer Academic Publishers, 1993, ISBN 0-7923-2382-3.
- V.G.Voinov, M.S.Nikulin, "Unbiased estimators and their applications. Vol.2: Multivariate case", Kluwer Academic Publishers, 1996, ISBN 0-7923-3939-8.