Completeness (statistics)
Encyclopedia
In statistics
, completeness is a property of a statistic
in relation to a model for a set of observed data. In essence, it is a condition which ensures that the parameters of the probability distribution representing the model can all be estimated on the basis of the statistic: it ensures that the distributions corresponding to different values of the parameters are distinct.
It is closely related to the idea of identifiability
, but in statistical theory
it is often found as a condition imposed on a sufficient statistic from which certain optimality results are derived.
X whose probability distribution belongs to a parametric family
of probability distributions Pθ parametrized by θ.
Formally, a statistic
s is a measurable function
of X; thus, a statistic s is evaluated on a random variable X, taking the value s(X), which is itself a random variable. A given realization of the random variable X(ω) is a data-point (datum), on which the statistic s takes the value s(X(ω)).
The statistic s is said to be complete for the distribution of X if for every measurable function g the following implication holds:
The statistic s is said to be boundedly complete if the implication holds for all bounded functions g.
of size n such that each Xi has the same Bernoulli distribution with parameter θ. Let T be the number of 1's observed in the sample. T is a statistic of X which has a Binomial distribution with parameters (n,θ). If the parameter space for θ is [0,1], then T is a complete statistic. To see this, note that
Observe also that neither p nor 1 − p can be 0. Hence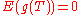
if and only if:
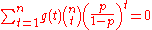
One denoting p/(1 − p) by r one gets:
First, observe that the range of r is all reals except for 0. Also, E(g(T)) is a polynomial
in r and, therefore, can only be identical to 0 if all coefficients are 0, that is, g(t) = 0 for all t.
It is important to notice that the result that all coefficients must be 0 was obtained because of the range of r. Had the parameter space been finite and with a number of elements smaller than n, it might be possible to solve the linear equations in g(t) obtained by substituting the values of r and get solutions different from 0. For example, if n = 1 and the parametric space is {0.5}, a single observation, T is not complete. Observe that, with the definition:
then, E(g(T)) = 0 although g(t) is not 0 for t = 0 nor for t = 1.
, identically distributed random variables, normally distributed with expectation θ and variance 1.
The sum
is a complete statistic for θ.
To show this, it is sufficient to demonstrate that there is no non-zero function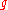
such that the expectation of
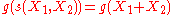
remains zero regardless of the value of θ.
That fact may be seen as follows. The probability distribution of X1 + X2 is normal with expectation 2θ and variance 2. Its probability density function in
is therefore proportional to
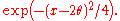
The expectation of g above would therefore be a constant times
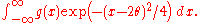
A bit of algebra reduces this to
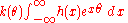
where k(θ) is nowhere zero and
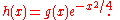
As a function of θ this is a two-sided Laplace transform of h(X), and cannot be identically zero unless h(x) is zero almost everywhere. The exponential is not zero, so this can only happen if g(x) is zero almost everywhere.
,
which states that if a statistic that is unbiased, complete and sufficient
for some parameter θ, then it is the best mean-unbiased estimator for θ. In other words, this statistic has a smaller expected loss for any convex
loss function; in many practice applications with the squared loss-function, it has a smaller mean squared error among any estimators with the same expected value
.
See also minimum-variance unbiased estimator
.
, which states that a statistic which is both boundedly complete and sufficient is independent
of any ancillary statistic
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, completeness is a property of a statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
in relation to a model for a set of observed data. In essence, it is a condition which ensures that the parameters of the probability distribution representing the model can all be estimated on the basis of the statistic: it ensures that the distributions corresponding to different values of the parameters are distinct.
It is closely related to the idea of identifiability
Identifiability
In statistics, identifiability is a property which a model must satisfy in order for inference to be possible. We say that the model is identifiable if it is theoretically possible to learn the true value of this model’s underlying parameter after obtaining an infinite number of observations from it...
, but in statistical theory
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
it is often found as a condition imposed on a sufficient statistic from which certain optimality results are derived.
Definition
Consider a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X whose probability distribution belongs to a parametric family
Parametric family
In mathematics and its applications, a parametric family or a parameterized family is a family of objects whose definitions depend on a set of parameters....
of probability distributions Pθ parametrized by θ.
Formally, a statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
s is a measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
of X; thus, a statistic s is evaluated on a random variable X, taking the value s(X), which is itself a random variable. A given realization of the random variable X(ω) is a data-point (datum), on which the statistic s takes the value s(X(ω)).
The statistic s is said to be complete for the distribution of X if for every measurable function g the following implication holds:
- E(g(s(X))) = 0 for all θ implies that Pθ(g(s(X)) = 0) = 1 for all θ.
The statistic s is said to be boundedly complete if the implication holds for all bounded functions g.
Example 1: Bernoulli model
The Bernoulli model admits a complete statistic. Let X be a random sampleRandom sample
In statistics, a sample is a subject chosen from a population for investigation; a random sample is one chosen by a method involving an unpredictable component...
of size n such that each Xi has the same Bernoulli distribution with parameter θ. Let T be the number of 1's observed in the sample. T is a statistic of X which has a Binomial distribution with parameters (n,θ). If the parameter space for θ is [0,1], then T is a complete statistic. To see this, note that
Observe also that neither p nor 1 − p can be 0. Hence
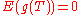if and only if: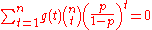One denoting p/(1 − p) by r one gets:
First, observe that the range of r is all reals except for 0. Also, E(g(T)) is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in r and, therefore, can only be identical to 0 if all coefficients are 0, that is, g(t) = 0 for all t.
It is important to notice that the result that all coefficients must be 0 was obtained because of the range of r. Had the parameter space been finite and with a number of elements smaller than n, it might be possible to solve the linear equations in g(t) obtained by substituting the values of r and get solutions different from 0. For example, if n = 1 and the parametric space is {0.5}, a single observation, T is not complete. Observe that, with the definition:
then, E(g(T)) = 0 although g(t) is not 0 for t = 0 nor for t = 1.
Example 2: Sum of normals
This example will show that, in a sample of size 2 from a normal distribution with known variance, the statistic X1+X2 is complete and sufficient. Suppose (X1, X2) are independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, identically distributed random variables, normally distributed with expectation θ and variance 1.
The sum
is a complete statistic for θ.
To show this, it is sufficient to demonstrate that there is no non-zero function
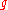such that the expectation of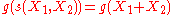remains zero regardless of the value of θ.
That fact may be seen as follows. The probability distribution of X1 + X2 is normal with expectation 2θ and variance 2. Its probability density function in
is therefore proportional to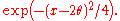The expectation of g above would therefore be a constant times
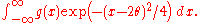
A bit of algebra reduces this to
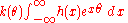
where k(θ) is nowhere zero and
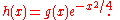
As a function of θ this is a two-sided Laplace transform of h(X), and cannot be identically zero unless h(x) is zero almost everywhere. The exponential is not zero, so this can only happen if g(x) is zero almost everywhere.
Relation to sufficient statistics
For some parametric families, a complete sufficient statistic does not exist. Also, a minimal sufficient statistic need not exist. (A case in which there is no minimal sufficient statistic was shown by Bahadur 1957. ) Under mild conditions, a minimal sufficient statistic does always exist. In particular, these conditions always hold if the random variables (associated with Pθ ) are all discrete or are all continuous.Importance of completeness
The notion of completeness has many applications in statistics, particularly in the following two theorems of mathematical statistics.Lehmann–Scheffé theorem
Completeness occurs in the Lehmann–Scheffé theoremLehmann–Scheffé theorem
In statistics, the Lehmann–Scheffé theorem is prominent in mathematical statistics, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation...
,
which states that if a statistic that is unbiased, complete and sufficient
Sufficiency (statistics)
In statistics, a sufficient statistic is a statistic which has the property of sufficiency with respect to a statistical model and its associated unknown parameter, meaning that "no other statistic which can be calculated from the same sample provides any additional information as to the value of...
for some parameter θ, then it is the best mean-unbiased estimator for θ. In other words, this statistic has a smaller expected loss for any convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
loss function; in many practice applications with the squared loss-function, it has a smaller mean squared error among any estimators with the same expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
.
See also minimum-variance unbiased estimator
Minimum-variance unbiased estimator
In statistics a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.The question of determining the UMVUE, if one exists, for a particular...
.
Basu's theorem
Bounded completeness occurs in Basu's theoremBasu's theorem
In statistics, Basu's theorem states that any boundedly complete sufficient statistic is independent of any ancillary statistic. This is a 1955 result of Debabrata Basu....
, which states that a statistic which is both boundedly complete and sufficient is independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of any ancillary statistic
Ancillary statistic
In statistics, an ancillary statistic is a statistic whose sampling distribution does not depend on which of the probability distributions among those being considered is the distribution of the statistical population from which the data were taken...
.