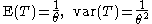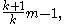Minimum-variance unbiased estimator
Encyclopedia
In statistics
a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator (UMVUE or MVUE) is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.
The question of determining the UMVUE, if one exists, for a particular problem is important for practical statistics, since less-than-optimal procedures would naturally be avoided, other things being equal. This has led to substantial development of statistical theory related to the problem of optimal estimation. While the particular specification of "optimal" here — requiring unbiasedness and measuring "goodness" using the variance
— may not always be what is wanted for any given practical situation, it is one where useful and generally applicable results can be found.
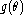 based on data
based on data 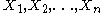 i.i.d. from some member of a family of densities
i.i.d. from some member of a family of densities 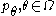 , where
, where 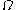 is the parameter space. An unbiased estimator
is the parameter space. An unbiased estimator  of
of  is UMVU if
is UMVU if 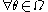 ,
,
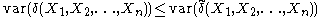
for any other unbiased estimator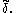
If an unbiased estimator of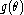 exists, then one can prove there is an essentially unique MVUE. Using the Rao–Blackwell theorem
exists, then one can prove there is an essentially unique MVUE. Using the Rao–Blackwell theorem
one can also prove that determining the MVUE is simply a matter of finding a complete sufficient statistic for the family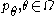 and conditioning any unbiased estimator on it.
and conditioning any unbiased estimator on it.
Further, by the Lehmann–Scheffé theorem
, an unbiased estimator that is a function of a complete, sufficient statistic is the UMVU estimator.
Put formally, suppose is unbiased for
is unbiased for 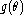 , and that
, and that 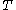 is a complete sufficient statistic for the family of densities. Then
is a complete sufficient statistic for the family of densities. Then

is the MVUE for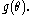
A Bayesian
analog is a Bayes estimator
, particularly with minimum mean square error (MMSE).
need not exist, but if it does and if it unbiased,
it is the MVUE. Since the mean squared error
(MSE) of an estimator δ is

the MVUE minimizes MSE among unbiased estimators. In some cases biased estimators have lower MSE because they have a smaller variance than does any unbiased estimator; see estimator bias.
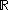
with density

and we wish to find the UMVU estimator of
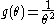
First we recognize that the density can be written as
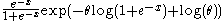
Which is an exponential family with sufficient statistic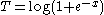 . In
. In
fact this is a full rank exponential family, and therefore is complete sufficient. See exponential family
is complete sufficient. See exponential family
for a derivation which shows
Therefore
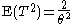
Clearly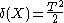 is unbiased, thus the UMVU estimator is
is unbiased, thus the UMVU estimator is
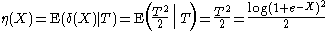
This example illustrates that an unbiased function of the complete sufficient statistic will be UMVU.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator (UMVUE or MVUE) is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.
The question of determining the UMVUE, if one exists, for a particular problem is important for practical statistics, since less-than-optimal procedures would naturally be avoided, other things being equal. This has led to substantial development of statistical theory related to the problem of optimal estimation. While the particular specification of "optimal" here — requiring unbiasedness and measuring "goodness" using the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
— may not always be what is wanted for any given practical situation, it is one where useful and generally applicable results can be found.
Definition
Consider estimation of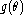 based on data
based on data 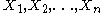 i.i.d. from some member of a family of densities
i.i.d. from some member of a family of densities 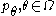 , where
, where 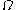 is the parameter space. An unbiased estimator
is the parameter space. An unbiased estimator  of
of  is UMVU if
is UMVU if 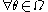 ,
,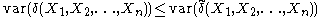
for any other unbiased estimator
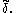
If an unbiased estimator of
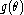 exists, then one can prove there is an essentially unique MVUE. Using the Rao–Blackwell theorem
exists, then one can prove there is an essentially unique MVUE. Using the Rao–Blackwell theoremRao–Blackwell theorem
In statistics, the Rao–Blackwell theorem, sometimes referred to as the Rao–Blackwell–Kolmogorov theorem, is a result which characterizes the transformation of an arbitrarily crude estimator into an estimator that is optimal by the mean-squared-error criterion or any of a variety of similar...
one can also prove that determining the MVUE is simply a matter of finding a complete sufficient statistic for the family
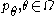 and conditioning any unbiased estimator on it.
and conditioning any unbiased estimator on it.Further, by the Lehmann–Scheffé theorem
Lehmann–Scheffé theorem
In statistics, the Lehmann–Scheffé theorem is prominent in mathematical statistics, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation...
, an unbiased estimator that is a function of a complete, sufficient statistic is the UMVU estimator.
Put formally, suppose
 is unbiased for
is unbiased for 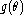 , and that
, and that 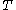 is a complete sufficient statistic for the family of densities. Then
is a complete sufficient statistic for the family of densities. Then
is the MVUE for
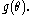
A Bayesian
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
analog is a Bayes estimator
Bayes estimator
In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function . Equivalently, it maximizes the posterior expectation of a utility function...
, particularly with minimum mean square error (MMSE).
Estimator selection
An efficient estimatorEfficiency (statistics)
In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
need not exist, but if it does and if it unbiased,
it is the MVUE. Since the mean squared error
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
(MSE) of an estimator δ is

the MVUE minimizes MSE among unbiased estimators. In some cases biased estimators have lower MSE because they have a smaller variance than does any unbiased estimator; see estimator bias.
Example
Consider the data to be a single observation from an absolutely continuous distribution on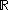
with density

and we wish to find the UMVU estimator of
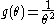
First we recognize that the density can be written as
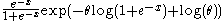
Which is an exponential family with sufficient statistic
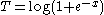 . In
. Infact this is a full rank exponential family, and therefore
 is complete sufficient. See exponential family
is complete sufficient. See exponential familyExponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
for a derivation which shows
Therefore
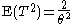
Clearly
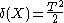 is unbiased, thus the UMVU estimator is
is unbiased, thus the UMVU estimator is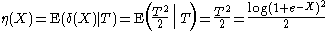
This example illustrates that an unbiased function of the complete sufficient statistic will be UMVU.
Other examples
- For a normal distribution with unknown mean and variance, the sample mean and (unbiased) sample variance are the MVUEs for the population mean and population variance.
- However, the sample standard deviationSample standard deviationA sample standard deviation is an estimate, based on a sample, of a population standard deviation. See:* Standard deviation#Estimation* Sample mean and sample covariance...
is not unbiased for the population standard deviation – see unbiased estimation of standard deviationUnbiased estimation of standard deviationThe question of unbiased estimation of a standard deviation arises in statistics mainly as question in statistical theory. Except in some important situations, outlined later, the task has little relevance to applications of statistics since its need is avoided by standard procedures, such as the...
. - Further, for other distributions the sample mean and sample variance are not in general MVUEs – for a uniform distributionUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
with unknown upper and lower bounds, the mid-range is the MVUE for the population mean.
- However, the sample standard deviation
- If k exemplars are chosen (without replacement) from a discrete uniform distribution over the set {1, 2, ..., N} with unknown upper bound N, the MVUE for N is
-
-
- where m is the sample maximum. This is a scaled and shifted (so unbiased) transform of the sample maximum, which is a sufficient and complete statistic. See German tank problemGerman tank problemIn the statistical theory of estimation, estimating the maximum of a uniform distribution is a common illustration of differences between estimation methods...
for details.
See also
- Best linear unbiased estimator (BLUE)
- Lehmann–Scheffé theoremLehmann–Scheffé theoremIn statistics, the Lehmann–Scheffé theorem is prominent in mathematical statistics, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation...
- U-statisticU-statisticIn statistical theory, a U-statistic is a class of statistics that is especially important in estimation theory. In elementary statistics, U-statistics arise naturally in producing minimum-variance unbiased estimators...