
U-statistic
Encyclopedia
In statistical theory
, a U-statistic is a class of statistics that is especially important in estimation theory
. In elementary statistics, U-statistics arise naturally in producing minimum-variance unbiased estimator
s. A mean-unbiased estimator
that is conditioned on the order statistics (of an sequence of independent and identically distributed random variables) becomes the minimum-variance unbiased estimator
, by the Rao-Blackwell theorem. Of even more importance is that the theory related to U-statistics allows a single theoretical framework to be used in non-parametric statistics
to prove results for a wide range of test-statistics and estimators relating to the asymptotic normality and to the variance (in finite samples) of such quantities. In addition the theory has applications to estimators which are not themselves U-statistics.
Suppose that a problem involves independent and identically-distributed random variables and that estimation of a certain parameter is required. Suppose that a simple unbiased estimate can be constructed based on only a few observations: this defines the basic estimator based on a given number of observations. For example, a single observation is itself an unbiased estimate of the mean and a pair of observations can be used to derive an unbiased estimate of the variance. The U-statistic based on this estimator is defined as the average (across all combinatorial selections of the given size from the full set of observations) of the basic estimator applied to the sub-samples.
Sen (1992) provides a review of the paper by Wassily Hoeffding
(1948), which introduced U-statistics and set out the theory relating to them, and in doing so Sen outlines the importance U-statistics have in statistical theory. Sen says "The impact of Hoeffding (1948) is overwhelming at the present time and is very likely to continue in the years to come". Note that the theory of U-statistics is not limited to the case of independent and identically-distributed random variables or to scalar random variables.
Let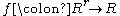 be a real-valued or complex-valued function of
be a real-valued or complex-valued function of  variables.
variables.
For each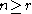 the associated U-statistic
the associated U-statistic 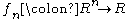 is
is
equal to the average over ordered samples of size
of size  of
of
the sample values .
.
In other words,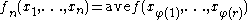 ,
,
the average being taken over distinct ordered samples of size taken from
taken from 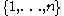 .
.
Each U-statistic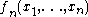 is necessarily a symmetric function
is necessarily a symmetric function
.
In other words, it bootstraps
a r-sample estimator to an n-sample estimator.
U-statistics are very natural in statistical work, particularly in Hoeffding's context of independent and identically-distributed random variables, or more generally for exchangeable sequences, such as in simple random sampling from a finite population, where the defining property is termed `inheritance on the average'.
Fisher's k-statistics and Tukey's polykays are examples of homogeneous polynomial
U-statistics
(Fisher, 1929; Tukey, 1950).
For a simple random sample φ of size n taken from a population of size N, the U-statistic has the property that the average over sample values ƒn(xφ) is exactly equal to the population value ƒN(x).
If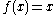 the U-statistic
the U-statistic 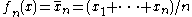 is the sample mean.
is the sample mean.
If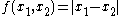 , the U-statistic is the mean pairwise deviation
, the U-statistic is the mean pairwise deviation
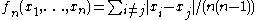 , defined for
, defined for 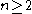 .
.
If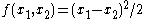 , the U-statistic is the sample variance
, the U-statistic is the sample variance
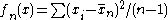
with divisor , defined for
, defined for 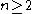 .
.
The third -statistic
-statistic 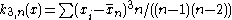 ,
,
the sample skewness
defined for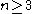 ,
,
is a U-statistic.
The following case highlights an important point. If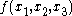 is the median
is the median
of three values,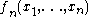 is not the median of
is not the median of  values. However, it is a minimum variance unbiased estimate of the expected value of the median of three values and in this application of the theory it is the population parameter defined as "the expected value of the median of three values" which is being estimated, not the median of the population. Similar estimates play a central role where the parameters of a family of probability distributions are being estimated by probability weighted moments or L-moments.
values. However, it is a minimum variance unbiased estimate of the expected value of the median of three values and in this application of the theory it is the population parameter defined as "the expected value of the median of three values" which is being estimated, not the median of the population. Similar estimates play a central role where the parameters of a family of probability distributions are being estimated by probability weighted moments or L-moments.
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
, a U-statistic is a class of statistics that is especially important in estimation theory
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
. In elementary statistics, U-statistics arise naturally in producing minimum-variance unbiased estimator
Minimum-variance unbiased estimator
In statistics a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.The question of determining the UMVUE, if one exists, for a particular...
s. A mean-unbiased estimator
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
that is conditioned on the order statistics (of an sequence of independent and identically distributed random variables) becomes the minimum-variance unbiased estimator
Minimum-variance unbiased estimator
In statistics a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.The question of determining the UMVUE, if one exists, for a particular...
, by the Rao-Blackwell theorem. Of even more importance is that the theory related to U-statistics allows a single theoretical framework to be used in non-parametric statistics
Non-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
to prove results for a wide range of test-statistics and estimators relating to the asymptotic normality and to the variance (in finite samples) of such quantities. In addition the theory has applications to estimators which are not themselves U-statistics.
Suppose that a problem involves independent and identically-distributed random variables and that estimation of a certain parameter is required. Suppose that a simple unbiased estimate can be constructed based on only a few observations: this defines the basic estimator based on a given number of observations. For example, a single observation is itself an unbiased estimate of the mean and a pair of observations can be used to derive an unbiased estimate of the variance. The U-statistic based on this estimator is defined as the average (across all combinatorial selections of the given size from the full set of observations) of the basic estimator applied to the sub-samples.
Sen (1992) provides a review of the paper by Wassily Hoeffding
Wassily Hoeffding
Wassily Hoeffding was an American statistician and probabilist...
(1948), which introduced U-statistics and set out the theory relating to them, and in doing so Sen outlines the importance U-statistics have in statistical theory. Sen says "The impact of Hoeffding (1948) is overwhelming at the present time and is very likely to continue in the years to come". Note that the theory of U-statistics is not limited to the case of independent and identically-distributed random variables or to scalar random variables.
Formal definition
The term U-statistic, due to Hoeffding (1948), is defined as follows.Let
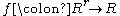 be a real-valued or complex-valued function of
be a real-valued or complex-valued function of  variables.
variables.For each
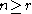 the associated U-statistic
the associated U-statistic 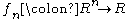 is
isequal to the average over ordered samples
 of size
of size  of
ofthe sample values
 .
.In other words,
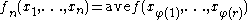 ,
,the average being taken over distinct ordered samples of size
 taken from
taken from 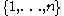 .
.Each U-statistic
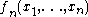 is necessarily a symmetric function
is necessarily a symmetric functionSymmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
.
In other words, it bootstraps
Bootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
a r-sample estimator to an n-sample estimator.
U-statistics are very natural in statistical work, particularly in Hoeffding's context of independent and identically-distributed random variables, or more generally for exchangeable sequences, such as in simple random sampling from a finite population, where the defining property is termed `inheritance on the average'.
Fisher's k-statistics and Tukey's polykays are examples of homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
U-statistics
(Fisher, 1929; Tukey, 1950).
For a simple random sample φ of size n taken from a population of size N, the U-statistic has the property that the average over sample values ƒn(xφ) is exactly equal to the population value ƒN(x).
Examples
Some examples:If
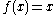 the U-statistic
the U-statistic 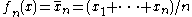 is the sample mean.
is the sample mean.If
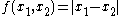 , the U-statistic is the mean pairwise deviation
, the U-statistic is the mean pairwise deviation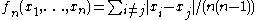 , defined for
, defined for 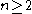 .
.If
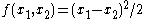 , the U-statistic is the sample variance
, the U-statistic is the sample variance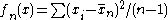
with divisor
 , defined for
, defined for 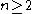 .
.The third
 -statistic
-statistic 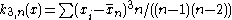 ,
,the sample skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
defined for
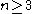 ,
,is a U-statistic.
The following case highlights an important point. If
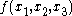 is the median
is the medianMedian
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of three values,
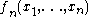 is not the median of
is not the median of  values. However, it is a minimum variance unbiased estimate of the expected value of the median of three values and in this application of the theory it is the population parameter defined as "the expected value of the median of three values" which is being estimated, not the median of the population. Similar estimates play a central role where the parameters of a family of probability distributions are being estimated by probability weighted moments or L-moments.
values. However, it is a minimum variance unbiased estimate of the expected value of the median of three values and in this application of the theory it is the population parameter defined as "the expected value of the median of three values" which is being estimated, not the median of the population. Similar estimates play a central role where the parameters of a family of probability distributions are being estimated by probability weighted moments or L-moments.

