German tank problem
Encyclopedia
In the statistical theory
of estimation
, estimating the maximum of a uniform distribution
is a common illustration of differences between estimation methods. The specific case of sampling without replacement from a discrete uniform distribution is known, in the English-speaking world, as the German tank problem, due to its application in World War II
to the estimation of the number of German tanks.
Estimating the population maximum based on a single sample yields divergent results, while the estimation based on multiple samples is an instructive practical estimation question whose answer is simple but not obvious.
is to determine the strength of an enemy force: in World War II, the Western Allies
wanted to estimate the number of tanks the Germans had, and approached this in two major ways: conventional intelligence gathering, and statistical estimation. The statistical approach proved to be far more accurate than conventional intelligence methods; the primary reference for the statistical approach is Ruggles & Brodie (1947).Ruggles & Brodie is largely a practical analysis and summary, not a mathematical one – the estimation problem is only mentioned in footnote 3 on page 82, where they estimate the maximum as "sample maximum + average gap". In some cases statistical analysis contradicted and substantially improved on conventional intelligence; in others, conventional intelligence and the statistical approach worked together, as in estimation of Panther tank
production, discussed below. Estimating production was not the only use of this serial number analysis; it was used to understand German production more generally, including number of factories, relative importance of factories, length of supply chain (based on lag between production and use), changes in production, and use of resources such as rubber.
To estimate the number of tanks produced up to a certain point, the Allies used the serial numbers on tanks. The principal numbers used were gearbox numbers, as these fell in two unbroken sequences. Chassis and engine numbers were also used, though their use were more complicated – various other components were used in the cross-checking of the analysis. Similar analyses were done on tires. which were observed to be sequentially numbered (i.e. 1, 2, 3, ..., N).The lower bound was unknown, but to simplify the discussion this detail is generally omitted, taking the lower bound as known to be 1.
showed the actual number to be 255.
Estimates for some specific months is given as:
Shortly before D-Day
, following rumors of large Panther tank
production collected by conventional intelligence, analysis of road wheels from two tanks (consisting of 48 wheels each, for 96 wheels total) yielded an estimate of 270 Panthers produced in February 1944, substantially more than had previously been suspected; German records after the war showed production for that month was 276. Specifically, analysis of the wheels yielded an estimate for the number of wheel molds; discussion with British road wheel makers then estimated the number of wheels that could be produced from this many molds.
Similar serial number analysis was used for other military equipment during World War II, most successfully for the V-2 rocket.
During World War II, German intelligence analyzed factory markings on Soviet military equipment, and during the Korean war
, factory markings on Soviet equipment was again analyzed. The Soviets also estimated German tank production during World War II.
In the 1980s, some Americans were given access to the production line of Israel’s Merkava
tanks. The production numbers were classified, but the tanks had serial numbers, allowing estimation of production.
), or simply produce random numbers and check them against the list of already assigned numbers; collisions are likely to occur unless the number of digits possible is more than twice as many as the number of digits in the number of objects produced (where the serial number can be in decimal, hexadecimal or indeed in any base); see birthday problem.As discussed in birthday attack
, one can expect a collision after 1.25√H numbers, if choosing from H possible outputs. This square root corresponds to half the digits. For example, the square root of a number with 100 digits is approximately a number with 50 digits in any base. For this, one may use a cryptographically secure pseudorandom number generator
. Less securely, to avoid lookup problems, one may use any pseudorandom number generator
with large period, which is guaranteed to avoid collisions. All these methods require a lookup table (or breaking the cypher) to back out from serial number to production order, which complicates use of serial numbers: one cannot simply recall a range of serial numbers, for instance, but instead must look them each up individually, or generate a list.
Alternatively, one can simply use sequential serial numbers and encrypt them, which allows easy decoding, but then there is a known-plaintext attack
: even if one starts from an arbitrary point, the plaintext has a pattern (namely, numbers are in sequence).
(estimating a single value for the total), the minimum-variance unbiased estimator
(MVUE, or UMVU estimator) is given by:In a continuous distribution, there is no −1.
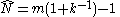
where m is the largest serial number observed (sample maximum) and k is the number of tanks observed (sample size
). Note that once a serial number has been observed, it is no longer in the pool and will not be observed again.
This has a variance of
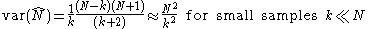
so a standard deviation
of approximately N/k, the (population) average size of a gap between samples; compare m/k above.
gives a value 16.5, which is close to the actual number of tanks, 15. Then suppose the officer spots an additional 2 tanks, neither of them #15. Now k = 6 and m remains 14. The formula gives a better estimate of 15.333...
the gap being added to compensate for the negative bias of the sample maximum as an estimator for the population maximum,The sample maximum is never more than the population maximum, but can be less, hence it is a biased estimator: it will tend to underestimate the population maximum. and written as
This can be visualized by imagining that the samples are evenly spaced throughout the range, with additional samples just outside the range at 0 and N + 1. If one starts with an initial gap being between 0 and the lowest sample (sample minimum), then the average gap between samples is m/k − 1; the −1 being because one does not count the samples themselves in computing the gap between samples.For example, the gap between 2 and 7 is (7 − 2) − 1 = 4, consisting of 3, 4, 5, and 6.
This philosophy is formalized and generalized in the method of maximum spacing estimation
.
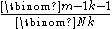, where 
is the binomial coefficient
.
The expected value of the sample maximum is
Solving for N gives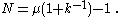
Since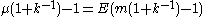
it follows that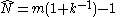
is an unbiased estimator of N.
To show that this is the UMVU estimator:
, such as confidence interval
s.
These are easily computed, based on the observation that the odds that k samples will fall in an interval covering p of the range (0 ≤ p ≤ 1) is pk (assuming in this section that draws are with replacement, to simplify computations; if draws are without replacement, this overstates the likelihood, and intervals will be overly conservative).
Thus the sampling distribution
of the quantile of the sample maximum is the graph x1/k from 0 to 1: the pth to qth quantile of the sample maximum m are the interval [p1/kN, q1/kN]. Inverting this yields the corresponding confidence interval for the population maximum of [m/q1/k, m/p1/k].
For example, taking the symmetric 95% interval p = 2.5% and q = 97.5% for k = 5 yields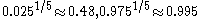
, so a confidence interval of approximately 
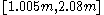. The lower bound is very close to m, so more informative is the asymmetric confidence interval from p = 5% to 100%; for k = 5 this yields 
so the interval [m, 1.82m].
More generally, the (downward biased) 95% confidence interval is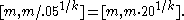
For a range of k, with the UMVU point estimator (plus 1 for legibility) for reference, this yields:
Immediate observations are:
Note that one cannot naively use m/k (or rather (m + m/k − 1)/k) as an estimate of the standard error
SE, as the standard error of an estimator is based on the population maximum (a parameter), and using an estimate to estimate the error in that very estimate is circular reasoning
.
approach to the German Tank Problem is to consider the conditional probability
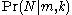that the number of enemy tanks is equal to 
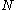, when 
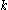serial numbers have been observed, and the largest of these is 
.
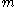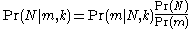
Then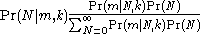
Assume that the prior probability
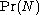is some discrete uniform distribution
, (where the Iverson bracket 
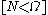means 1 when 
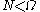and 0 otherwise). The upper limit 
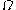must be finite, because 
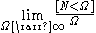is not a probability mass function of 
.
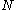Then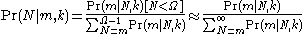
If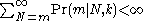
, then the approximation is adequate, and the unwelcome variable 
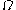vanishes from the expressions.
The conditional probability that the largest tank number observed is equal to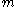
, when the number of enemy tanks is equal to 
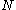, and 
enemy tanks has been observed, is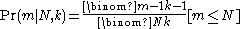
where the binomial coefficient
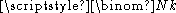is the number of 
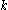-sized samples from an 
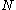-sized population.
For k≥1 the mode
of the distribution of the number of enemy tanks is m.
For k≥2, the probability that the number of enemy tanks is equal to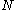
, is 
, and the probability that the number of enemy tanks is greater than 
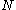, is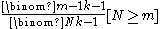 
.
For k≥3,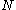
has the finite mean value 
.
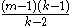For k≥4,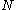
has the finite standard deviation
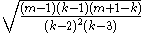
If tank numbers 2, 6, 7, and 14 were identified, then the posterior probability mass function is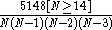
. The mean value of N is 19.5 and the standard deviation of N is 10.4, so we estimate that the enemy has got 20 tanks, give or take 10. Of course we still know that they have got at least 14 tanks. The distribution has positive skewness
.
The following important formula from Binomial coefficient#Identities involving binomial coefficients is used below for simplifying series
relating to the German Tank Problem.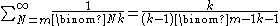
This is the conditional probability mass function of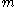
.
When considered a function of N for fixed m this is a likelihood function.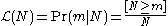
.
The maximum likelihood
estimate for N is N0 = m.
The total likelihood is a infinite, being a tail of the harmonic series
.
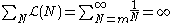
but
where
is the harmonic number.
The probability mass function
of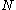
depends explicitly on the prior limit 
:
.
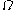The mean value of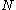
is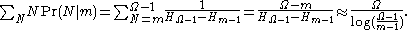
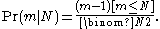
When considered a function of N for fixed m this is a likelihood function
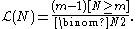
The total likelihood is
.
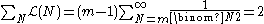and the probability mass function
is
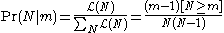
The median
satisfies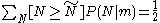
so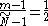
and so the median is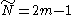
but the mean value of N is infinite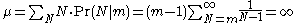
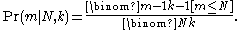
The likelihood function of N is the same expression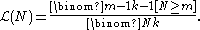
The total likelihood is finite for k ≥ 2: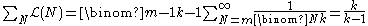
The probability mass function
of N is the probability that the number of enemy tanks is = N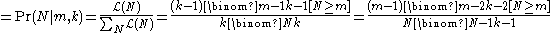
The cumulative distribution function
of N is the probability that the number of enemy tanks is ≤ N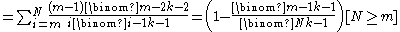
The expected number of enemy tanks is
The variance to mean ratio is computed like this.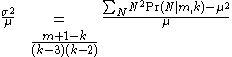
and the standard deviation
is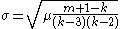
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
of estimation
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
, estimating the maximum of a uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
is a common illustration of differences between estimation methods. The specific case of sampling without replacement from a discrete uniform distribution is known, in the English-speaking world, as the German tank problem, due to its application in World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
to the estimation of the number of German tanks.
Estimating the population maximum based on a single sample yields divergent results, while the estimation based on multiple samples is an instructive practical estimation question whose answer is simple but not obvious.
Historical problem
In wartime, a key goal of military intelligenceMilitary intelligence
Military intelligence is a military discipline that exploits a number of information collection and analysis approaches to provide guidance and direction to commanders in support of their decisions....
is to determine the strength of an enemy force: in World War II, the Western Allies
Western Allies
The Western Allies were a political and geographic grouping among the Allied Powers of the Second World War. It generally includes the United Kingdom and British Commonwealth, the United States, France and various other European and Latin American countries, but excludes China, the Soviet Union,...
wanted to estimate the number of tanks the Germans had, and approached this in two major ways: conventional intelligence gathering, and statistical estimation. The statistical approach proved to be far more accurate than conventional intelligence methods; the primary reference for the statistical approach is Ruggles & Brodie (1947).Ruggles & Brodie is largely a practical analysis and summary, not a mathematical one – the estimation problem is only mentioned in footnote 3 on page 82, where they estimate the maximum as "sample maximum + average gap". In some cases statistical analysis contradicted and substantially improved on conventional intelligence; in others, conventional intelligence and the statistical approach worked together, as in estimation of Panther tank
Panther tank
Panther is the common name of a medium tank fielded by Nazi Germany in World War II that served from mid-1943 to the end of the European war in 1945. It was intended as a counter to the T-34, and to replace the Panzer III and Panzer IV; while never replacing the latter, it served alongside it as...
production, discussed below. Estimating production was not the only use of this serial number analysis; it was used to understand German production more generally, including number of factories, relative importance of factories, length of supply chain (based on lag between production and use), changes in production, and use of resources such as rubber.
To estimate the number of tanks produced up to a certain point, the Allies used the serial numbers on tanks. The principal numbers used were gearbox numbers, as these fell in two unbroken sequences. Chassis and engine numbers were also used, though their use were more complicated – various other components were used in the cross-checking of the analysis. Similar analyses were done on tires. which were observed to be sequentially numbered (i.e. 1, 2, 3, ..., N).The lower bound was unknown, but to simplify the discussion this detail is generally omitted, taking the lower bound as known to be 1.
Specific data
According to conventional Allied intelligence estimates the Germans were producing around 1,400 tanks a month between June 1940 and September 1942. Applying the above formula to the serial numbers of captured German tanks, (both serviceable and destroyed) the number was calculated to be 256 a month. After the war, captured German production figures from the ministry of Albert SpeerAlbert Speer
Albert Speer, born Berthold Konrad Hermann Albert Speer, was a German architect who was, for a part of World War II, Minister of Armaments and War Production for the Third Reich. Speer was Adolf Hitler's chief architect before assuming ministerial office...
showed the actual number to be 255.
Estimates for some specific months is given as:
| Month | Statistical estimate | Intelligence estimate | German records |
| June 1940 | 169 | 1000 | 122 |
| June 1941 | 244 | 1550 | 271 |
| August 1942 | 327 | 1550 | 342 |
Shortly before D-Day
D-Day
D-Day is a term often used in military parlance to denote the day on which a combat attack or operation is to be initiated. "D-Day" often represents a variable, designating the day upon which some significant event will occur or has occurred; see Military designation of days and hours for similar...
, following rumors of large Panther tank
Panther tank
Panther is the common name of a medium tank fielded by Nazi Germany in World War II that served from mid-1943 to the end of the European war in 1945. It was intended as a counter to the T-34, and to replace the Panzer III and Panzer IV; while never replacing the latter, it served alongside it as...
production collected by conventional intelligence, analysis of road wheels from two tanks (consisting of 48 wheels each, for 96 wheels total) yielded an estimate of 270 Panthers produced in February 1944, substantially more than had previously been suspected; German records after the war showed production for that month was 276. Specifically, analysis of the wheels yielded an estimate for the number of wheel molds; discussion with British road wheel makers then estimated the number of wheels that could be produced from this many molds.
Similar analyses
During World War II, German intelligence analyzed factory markings on Soviet military equipment, and during the Korean war
Korean War
The Korean War was a conventional war between South Korea, supported by the United Nations, and North Korea, supported by the People's Republic of China , with military material aid from the Soviet Union...
, factory markings on Soviet equipment was again analyzed. The Soviets also estimated German tank production during World War II.
In the 1980s, some Americans were given access to the production line of Israel’s Merkava
Merkava
The Merkava is a main battle tank used by the Israel Defense Forces. The tank began development in 1974 and was first introduced in 1978. Four main versions of the tank have been deployed. It was first used extensively in the 1982 Lebanon War...
tanks. The production numbers were classified, but the tanks had serial numbers, allowing estimation of production.
Countermeasures
To prevent serial number analysis, one can most simply not include serial numbers, or reduce auxiliary information that can be usable. Alternatively, one can design serial numbers that resist cryptanalysis, most effectively by randomly choosing numbers without replacement from a list that is much larger than the number of objects you produce (compare the one-time padOne-time pad
In cryptography, the one-time pad is a type of encryption, which has been proven to be impossible to crack if used correctly. Each bit or character from the plaintext is encrypted by a modular addition with a bit or character from a secret random key of the same length as the plaintext, resulting...
), or simply produce random numbers and check them against the list of already assigned numbers; collisions are likely to occur unless the number of digits possible is more than twice as many as the number of digits in the number of objects produced (where the serial number can be in decimal, hexadecimal or indeed in any base); see birthday problem.As discussed in birthday attack
Birthday attack
A birthday attack is a type of cryptographic attack that exploits the mathematics behind the birthday problem in probability theory. This attack can be used to abuse communication between two or more parties...
, one can expect a collision after 1.25√H numbers, if choosing from H possible outputs. This square root corresponds to half the digits. For example, the square root of a number with 100 digits is approximately a number with 50 digits in any base. For this, one may use a cryptographically secure pseudorandom number generator
Cryptographically secure pseudorandom number generator
A cryptographically secure pseudo-random number generator is a pseudo-random number generator with properties that make it suitable for use in cryptography.Many aspects of cryptography require random numbers, for example:...
. Less securely, to avoid lookup problems, one may use any pseudorandom number generator
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
with large period, which is guaranteed to avoid collisions. All these methods require a lookup table (or breaking the cypher) to back out from serial number to production order, which complicates use of serial numbers: one cannot simply recall a range of serial numbers, for instance, but instead must look them each up individually, or generate a list.
Alternatively, one can simply use sequential serial numbers and encrypt them, which allows easy decoding, but then there is a known-plaintext attack
Known-plaintext attack
The known-plaintext attack is an attack model for cryptanalysis where the attacker has samples of both the plaintext , and its encrypted version . These can be used to reveal further secret information such as secret keys and code books...
: even if one starts from an arbitrary point, the plaintext has a pattern (namely, numbers are in sequence).
Minimum-variance unbiased estimator
For point estimationPoint estimation
In statistics, point estimation involves the use of sample data to calculate a single value which is to serve as a "best guess" or "best estimate" of an unknown population parameter....
(estimating a single value for the total), the minimum-variance unbiased estimator
Minimum-variance unbiased estimator
In statistics a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.The question of determining the UMVUE, if one exists, for a particular...
(MVUE, or UMVU estimator) is given by:In a continuous distribution, there is no −1.
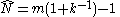
where m is the largest serial number observed (sample maximum) and k is the number of tanks observed (sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
). Note that once a serial number has been observed, it is no longer in the pool and will not be observed again.
This has a variance of
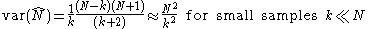
so a standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of approximately N/k, the (population) average size of a gap between samples; compare m/k above.
Example
Suppose there are 15 tanks, numbered 1, 2, 3, ..., 15. An intelligence officer has spotted tanks 2, 6, 7, 14. Using the above formula, the values for m and k would be 14 and 4, respectively. The formula gives a value 16.5, which is close to the actual number of tanks, 15. Then suppose the officer spots an additional 2 tanks, neither of them #15. Now k = 6 and m remains 14. The formula gives a better estimate of 15.333...Intuition
The formula may be understood intuitively as:- "The sample maximum plus the average gap between observations in the sample",
the gap being added to compensate for the negative bias of the sample maximum as an estimator for the population maximum,The sample maximum is never more than the population maximum, but can be less, hence it is a biased estimator: it will tend to underestimate the population maximum. and written as
This can be visualized by imagining that the samples are evenly spaced throughout the range, with additional samples just outside the range at 0 and N + 1. If one starts with an initial gap being between 0 and the lowest sample (sample minimum), then the average gap between samples is m/k − 1; the −1 being because one does not count the samples themselves in computing the gap between samples.For example, the gap between 2 and 7 is (7 − 2) − 1 = 4, consisting of 3, 4, 5, and 6.
This philosophy is formalized and generalized in the method of maximum spacing estimation
Maximum spacing estimation
In statistics, maximum spacing estimation , or maximum product of spacing estimation , is a method for estimating the parameters of a univariate statistical model...
.
Derivation
The probability that the sample maximum equals m is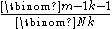, where is the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.
The expected value of the sample maximum is
Solving for N gives
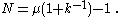
Since
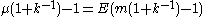it follows that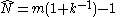is an unbiased estimator of N.
To show that this is the UMVU estimator:
- One first shows that the sample maximum is a sufficient statistic for the population maximum, using a method similar to that detailed at sufficiency: uniform distribution (but for the German tank problem we must exclude the outcomes in which a serial number occurs twice in the sample);
- Next, one shows that it is a complete statistic.
- Then the Lehmann–Scheffé theoremLehmann–Scheffé theoremIn statistics, the Lehmann–Scheffé theorem is prominent in mathematical statistics, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation...
states that the sample maximum, corrected for bias as above to be unbiased, is the UMVU estimator.
Confidence intervals
Instead of, or in addition to, point estimation, one can do interval estimationInterval estimation
In statistics, interval estimation is the use of sample data to calculate an interval of possible values of an unknown population parameter, in contrast to point estimation, which is a single number. Neyman identified interval estimation as distinct from point estimation...
, such as confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s.
These are easily computed, based on the observation that the odds that k samples will fall in an interval covering p of the range (0 ≤ p ≤ 1) is pk (assuming in this section that draws are with replacement, to simplify computations; if draws are without replacement, this overstates the likelihood, and intervals will be overly conservative).
Thus the sampling distribution
Sampling distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference...
of the quantile of the sample maximum is the graph x1/k from 0 to 1: the pth to qth quantile of the sample maximum m are the interval [p1/kN, q1/kN]. Inverting this yields the corresponding confidence interval for the population maximum of [m/q1/k, m/p1/k].
For example, taking the symmetric 95% interval p = 2.5% and q = 97.5% for k = 5 yields
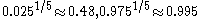, so a confidence interval of approximately 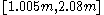. The lower bound is very close to m, so more informative is the asymmetric confidence interval from p = 5% to 100%; for k = 5 this yields so the interval [m, 1.82m].More generally, the (downward biased) 95% confidence interval is
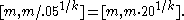For a range of k, with the UMVU point estimator (plus 1 for legibility) for reference, this yields:
| k | point estimate | confidence interval |
|---|---|---|
| 1 |  |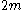
 |
| 2 |  |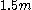
 |
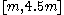| 5 |  |
 |
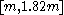| 10 |  |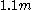
 |
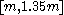| 20 |  |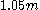
 |
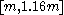Immediate observations are:
- For small sample sizes, the confidence interval is very wide, reflecting great uncertainty in the estimate.
- The range shrinks rapidly, reflecting the exponentially decaying likelihood that all samples will be significantly below the maximum.
- The confidence interval exhibits positive skew, as N can never be below the sample maximum, but can potentially be arbitrarily high above it.
Note that one cannot naively use m/k (or rather (m + m/k − 1)/k) as an estimate of the standard error
Standard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
SE, as the standard error of an estimator is based on the population maximum (a parameter), and using an estimate to estimate the error in that very estimate is circular reasoning
Circular reasoning
Circular reasoning, or in other words, paradoxical thinking, is a type of formal logical fallacy in which the proposition to be proved is assumed implicitly or explicitly in one of the premises. For example:"Only an untrustworthy person would run for office...
.
Summary
The Bayesian inferenceBayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
approach to the German Tank Problem is to consider the conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
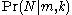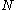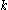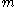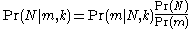
that the number of enemy tanks is equal to , when serial numbers have been observed, and the largest of these is .Then
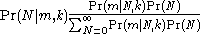
Assume that the prior probability
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
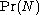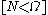is some discrete uniform distribution, (where the Iverson bracket means 1 when 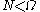and 0 otherwise). The upper limit 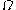must be finite, because 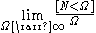is not a probability mass function of 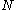.Then
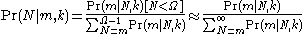
If
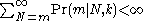, then the approximation is adequate, and the unwelcome variable 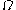vanishes from the expressions.The conditional probability that the largest tank number observed is equal to
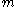, when the number of enemy tanks is equal to 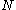, and enemy tanks has been observed, is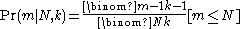where the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
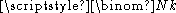is the number of 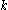-sized samples from an 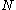-sized population.For k≥1 the mode
Mode
Mode may mean:* Transport mode, a means of transportation* Block cipher modes of operation, in cryptography* A technocomplex of stone tools...
of the distribution of the number of enemy tanks is m.
For k≥2, the probability that the number of enemy tanks is equal to
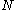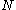, is , and the probability that the number of enemy tanks is greater than , is 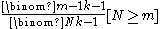.For k≥3,
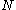has the finite mean value 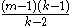.For k≥4,
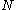has the finite standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
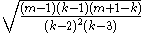
If tank numbers 2, 6, 7, and 14 were identified, then the posterior probability mass function is
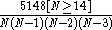. The mean value of N is 19.5 and the standard deviation of N is 10.4, so we estimate that the enemy has got 20 tanks, give or take 10. Of course we still know that they have got at least 14 tanks. The distribution has positive skewnessSkewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
.
The following important formula from Binomial coefficient#Identities involving binomial coefficients is used below for simplifying series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
relating to the German Tank Problem.
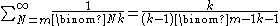
One tank
If you observe one tank randomly out of a population of N tanks, you get serial number m with probability 1/N for m ≤ N, and zero probability for m > N. This is writtenThis is the conditional probability mass function of
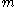.When considered a function of N for fixed m this is a likelihood function.
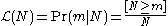.The maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate for N is N0 = m.
The total likelihood is a infinite, being a tail of the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
.
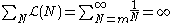
but
where
is the harmonic number.The probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
of
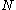depends explicitly on the prior limit 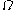:.The mean value of
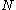is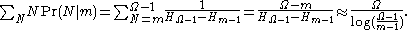Two tanks
If you observe two tanks rather than one, then the probability that the larger of the observed two serial numbers is equal to m, is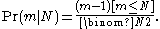When considered a function of N for fixed m this is a likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
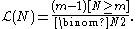
The total likelihood is
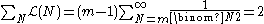.and the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
is
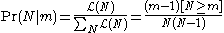
The median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
satisfies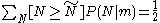so
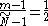
and so the median is
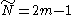
but the mean value of N is infinite
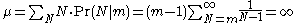
Many tanks
The conditional probability that the largest of k observations taken from the serial numbers {1,...,N}, is equal to m, is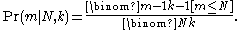The likelihood function of N is the same expression
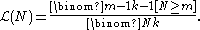
The total likelihood is finite for k ≥ 2:
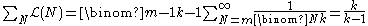
The probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
of N is the probability that the number of enemy tanks is = N
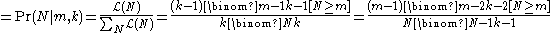
The cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of N is the probability that the number of enemy tanks is ≤ N
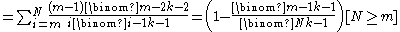
The expected number of enemy tanks is
The variance to mean ratio is computed like this.
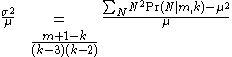
and the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
is
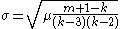
See also
- Capture-recapture, other method of estimating population size
- Maximum spacing estimationMaximum spacing estimationIn statistics, maximum spacing estimation , or maximum product of spacing estimation , is a method for estimating the parameters of a univariate statistical model...
, which generalizes the intuition of "assume uniformly distributed"
Other discussions of the estimation
- Maximum likelihood#Bias
- Bias of an estimator#Maximum of a discrete uniform distribution
- Likelihood function#Example 5