Pseudorandom number generator
Encyclopedia
A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm
for generating a sequence of numbers that approximates the properties of random numbers. The sequence is not truly random in that it is completely determined by a relatively small set of initial values, called the PRNG's state, which includes a truly random seed
. Although sequences that are closer to truly random can be generated using hardware random number generator
s, pseudorandom numbers are important in practice for their speed in number generation and their reproducibility, and they are thus central in applications such as simulations (e.g., of physical systems with the Monte Carlo method
), in cryptography
, and in procedural generation
. Good statistical properties are a central requirement for the output of a PRNG, and common classes of suitable algorithms include linear congruential generator
s, lagged Fibonacci generator
s, and linear feedback shift register
s. Cryptographic applications require the output to also be unpredictable, and more elaborate designs, which do not inherit the linearity of simpler solutions, are needed. More recent instances of PRNGs with strong randomness guarantees are based on computational hardness assumptions, and include the Blum Blum Shub, Fortuna
, and Mersenne Twister algorithms.
In general, careful mathematical analysis is required to have any confidence that a PRNG generates numbers that are sufficiently "random" to suit the intended use. John von Neumann
cautioned about the misinterpretation of a PRNG as a truly random generator, and joked that "Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin."Robert R. Coveyou of Oak Ridge National Laboratory
once titled an article, "The generation of random numbers is too important to be left to chance."
. It will always produce the same sequence thereafter when initialized with that state. The maximum length of the sequence before it begins to repeat is determined by the size of the state, measured in bit
s. However, since the length of the maximum period potentially doubles with each bit of 'state' added, it is easy to build PRNGs with periods long enough for many practical applications.
If a PRNG's internal state contains n bits, its period can be no longer than 2n results, and may be much shorter. For some PRNGs the period length can be calculated without walking through the whole period. Linear Feedback Shift Registers (LFSRs)
are usually chosen to have periods of exactly 2n−1. Linear congruential generator
s have periods that can be calculated by factoring. Mixes (no restrictions) have periods of about 2n/2 on average, usually after walking through a nonrepeating starting sequence. Mixes that are reversible (permutations) have periods of about 2n−1 on average, and the period will always include the original internal state (e.g. http://www.inference.phy.cam.ac.uk/mackay/itila/cycles.pdf). Although PRNGs will repeat their results after they reach the end of their period, a repeated result does not imply that the end of the period has been reached, since its internal state may be larger than its output; this is particularly obvious with PRNGs with a 1-bit output.
Most pseudorandom generator algorithms produce sequences which are uniformly distributed by any of several tests. It is an open question, and one central to the theory and practice of cryptography
, whether there is any way to distinguish the output of a high-quality PRNG from a truly random sequence without knowing the algorithm(s) used and the state with which it was initialized. The security of most cryptographic algorithms and protocols using PRNGs is based on the assumption that it is infeasible to distinguish use of a suitable PRNG from use of a truly random sequence. The simplest examples of this dependency are stream cipher
s, which (most often) work by exclusive or-ing the plaintext
of a message with the output of a PRNG, producing ciphertext
. The design of cryptographically adequate PRNGs is extremely difficult, because they must meet additional criteria (see below). The size of its period is an important factor in the cryptographic suitability of a PRNG, but not the only one.
Defects exhibited by flawed PRNGs range from unnoticeable (and unknown) to very obvious. An example was the RANDU random number algorithm used for decades on mainframe computer
s. It was seriously flawed, but its inadequacy went undetected for a very long time. In many fields, much research work of that period which relied on random selection or on Monte Carlo
style simulations, or in other ways, is less reliable than it might have been as a result.
in 1946, is known as the middle-square method
. The algorithm is as follows: take any number, square it, remove the middle digits of the resulting number as the "random number", then use that number as the seed for the next iteration. For example, squaring the number "1111" yields "1234321", which can be written as "01234321", an 8-digit number being the square of a 4-digit number. This gives "2343" as the "random" number. Repeating this procedure gives "4896" as the next result, and so on. Von Neumann used 10 digit numbers, but the process was the same.
A problem with the "middle square" method is that all sequences eventually repeat themselves, some very quickly, such as "0000". Von Neumann was aware of this, but he found the approach sufficient for his purposes, and was worried that mathematical "fixes" would simply hide errors rather than remove them.
Von Neumann judged hardware random number generators unsuitable, for, if they did not record the output generated, they could not later be tested for errors. If they did record their output, they would exhaust the limited computer memories available then, and so the computer's ability to read and write numbers. If the numbers were written to cards, they would take very much longer to write and read. On the ENIAC
computer he was using, the "middle square" method generated numbers at a rate some hundred times faster than reading numbers in from punched card
s.
The middle-square method has since been supplanted by more elaborate generators.
SFMT, SIMD-oriented Fast Mersenne Twister, a variant of Mersenne Twister, is faster even if it's not compiled with SIMD
support.http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/SFMT/speed.html
The native Mersenne Twister is not considered suitable for use in all cryptographic
applications. A variant of Mersenne Twister has been proposed as a cryptographic cipher. http://eprint.iacr.org/2005/165.pdf
applications is called a cryptographically secure PRNG (CSPRNG). A requirement for a CSPRNG is that an adversary not knowing the seed has only negligible advantage
in distinguishing the generator's output sequence from a random sequence. In other words, while a PRNG is only required to pass certain statistical tests, a CSPRNG must pass all statistical tests that are restricted to polynomial time in the size of the seed. Though such property cannot be proven, strong evidence may be provided by reducing the CSPRNG to a problem
that is assumed to be hard, such as integer factorization
. In general, years of review may be required before an algorithm can be certified as a CSPRNG.
Some classes of CSPRNGs include the following:
(BSI) has established four criteria for quality of deterministic random number generators. They are summarized here:
For cryptographic applications, only generators meeting the K3 or K4 standard are acceptable.
PRNG and a function that relates the two distributions.
First, one needs the cumulative distribution function
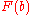of the target distribution 
:
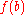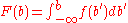
Note that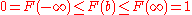
. Using a random number c from a uniform distribution as the probability density to "pass by", we get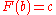
so that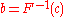
is a number randomly selected from distribution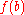
.
For example, the inverse of cumulative Gaussian distribution
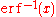with an ideal uniform PRNG with range (0, 1) as input 
would produce a sequence of (positive only) values with a Gaussian distribution; however
Similar considerations apply to generating other non-uniform distributions such as Rayleigh and Poisson
.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for generating a sequence of numbers that approximates the properties of random numbers. The sequence is not truly random in that it is completely determined by a relatively small set of initial values, called the PRNG's state, which includes a truly random seed
Random seed
A random seed is a number used to initialize a pseudorandom number generator.The choice of a good random seed is crucial in the field of computer security...
. Although sequences that are closer to truly random can be generated using hardware random number generator
Hardware random number generator
In computing, a hardware random number generator is an apparatus that generates random numbers from a physical process. Such devices are often based on microscopic phenomena that generate a low-level, statistically random "noise" signal, such as thermal noise or the photoelectric effect or other...
s, pseudorandom numbers are important in practice for their speed in number generation and their reproducibility, and they are thus central in applications such as simulations (e.g., of physical systems with the Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
), in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, and in procedural generation
Procedural generation
Procedural generation is a widely used term in the production of media; it refers to content generated algorithmically rather than manually. Often, this means creating content on the fly rather than prior to distribution...
. Good statistical properties are a central requirement for the output of a PRNG, and common classes of suitable algorithms include linear congruential generator
Linear congruential generator
A Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
s, lagged Fibonacci generator
Lagged Fibonacci generator
A Lagged Fibonacci generator is an example of a pseudorandom number generator. This class of random number generator is aimed at being an improvement on the 'standard' linear congruential generator...
s, and linear feedback shift register
Linear feedback shift register
A linear feedback shift register is a shift register whose input bit is a linear function of its previous state.The most commonly used linear function of single bits is XOR...
s. Cryptographic applications require the output to also be unpredictable, and more elaborate designs, which do not inherit the linearity of simpler solutions, are needed. More recent instances of PRNGs with strong randomness guarantees are based on computational hardness assumptions, and include the Blum Blum Shub, Fortuna
Fortuna (PRNG)
Fortuna is a cryptographically secure pseudorandom number generator devised by Bruce Schneier and Niels Ferguson. It is named after Fortuna, the Roman goddess of chance.- Design :Fortuna is a family of secure PRNGs; its design...
, and Mersenne Twister algorithms.
In general, careful mathematical analysis is required to have any confidence that a PRNG generates numbers that are sufficiently "random" to suit the intended use. John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
cautioned about the misinterpretation of a PRNG as a truly random generator, and joked that "Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin."Robert R. Coveyou of Oak Ridge National Laboratory
Oak Ridge National Laboratory
Oak Ridge National Laboratory is a multiprogram science and technology national laboratory managed for the United States Department of Energy by UT-Battelle. ORNL is the DOE's largest science and energy laboratory. ORNL is located in Oak Ridge, Tennessee, near Knoxville...
once titled an article, "The generation of random numbers is too important to be left to chance."
Periodicity
A PRNG can be started from an arbitrary starting state using a seed stateRandom seed
A random seed is a number used to initialize a pseudorandom number generator.The choice of a good random seed is crucial in the field of computer security...
. It will always produce the same sequence thereafter when initialized with that state. The maximum length of the sequence before it begins to repeat is determined by the size of the state, measured in bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s. However, since the length of the maximum period potentially doubles with each bit of 'state' added, it is easy to build PRNGs with periods long enough for many practical applications.
If a PRNG's internal state contains n bits, its period can be no longer than 2n results, and may be much shorter. For some PRNGs the period length can be calculated without walking through the whole period. Linear Feedback Shift Registers (LFSRs)
Linear feedback shift register
A linear feedback shift register is a shift register whose input bit is a linear function of its previous state.The most commonly used linear function of single bits is XOR...
are usually chosen to have periods of exactly 2n−1. Linear congruential generator
Linear congruential generator
A Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
s have periods that can be calculated by factoring. Mixes (no restrictions) have periods of about 2n/2 on average, usually after walking through a nonrepeating starting sequence. Mixes that are reversible (permutations) have periods of about 2n−1 on average, and the period will always include the original internal state (e.g. http://www.inference.phy.cam.ac.uk/mackay/itila/cycles.pdf). Although PRNGs will repeat their results after they reach the end of their period, a repeated result does not imply that the end of the period has been reached, since its internal state may be larger than its output; this is particularly obvious with PRNGs with a 1-bit output.
Most pseudorandom generator algorithms produce sequences which are uniformly distributed by any of several tests. It is an open question, and one central to the theory and practice of cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, whether there is any way to distinguish the output of a high-quality PRNG from a truly random sequence without knowing the algorithm(s) used and the state with which it was initialized. The security of most cryptographic algorithms and protocols using PRNGs is based on the assumption that it is infeasible to distinguish use of a suitable PRNG from use of a truly random sequence. The simplest examples of this dependency are stream cipher
Stream cipher
In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
s, which (most often) work by exclusive or-ing the plaintext
Plaintext
In cryptography, plaintext is information a sender wishes to transmit to a receiver. Cleartext is often used as a synonym. Before the computer era, plaintext most commonly meant message text in the language of the communicating parties....
of a message with the output of a PRNG, producing ciphertext
Ciphertext
In cryptography, ciphertext is the result of encryption performed on plaintext using an algorithm, called a cipher. Ciphertext is also known as encrypted or encoded information because it contains a form of the original plaintext that is unreadable by a human or computer without the proper cipher...
. The design of cryptographically adequate PRNGs is extremely difficult, because they must meet additional criteria (see below). The size of its period is an important factor in the cryptographic suitability of a PRNG, but not the only one.
Problems with deterministic generators
In practice, the output from many common PRNGs exhibit artifacts which cause them to fail statistical pattern detection tests. These include:- Shorter than expected periods for some seed states (such seed states may be called 'weak' in this context);
- Lack of uniformity of distribution for large amounts of generated numbers;
- Correlation of successive values;
- Poor dimensional distribution of the output sequence;
- The distances between where certain values occur are distributed differently from those in a random sequence distribution.
Defects exhibited by flawed PRNGs range from unnoticeable (and unknown) to very obvious. An example was the RANDU random number algorithm used for decades on mainframe computer
Mainframe computer
Mainframes are powerful computers used primarily by corporate and governmental organizations for critical applications, bulk data processing such as census, industry and consumer statistics, enterprise resource planning, and financial transaction processing.The term originally referred to the...
s. It was seriously flawed, but its inadequacy went undetected for a very long time. In many fields, much research work of that period which relied on random selection or on Monte Carlo
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
style simulations, or in other ways, is less reliable than it might have been as a result.
Early approaches
An early computer-based PRNG, suggested by John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
in 1946, is known as the middle-square method
Middle-square method
In mathematics, the middle-square method is a method of generating pseudorandom numbers. In practice it is not a good method, since its period is usually very short and it has some crippling weaknesses...
. The algorithm is as follows: take any number, square it, remove the middle digits of the resulting number as the "random number", then use that number as the seed for the next iteration. For example, squaring the number "1111" yields "1234321", which can be written as "01234321", an 8-digit number being the square of a 4-digit number. This gives "2343" as the "random" number. Repeating this procedure gives "4896" as the next result, and so on. Von Neumann used 10 digit numbers, but the process was the same.
A problem with the "middle square" method is that all sequences eventually repeat themselves, some very quickly, such as "0000". Von Neumann was aware of this, but he found the approach sufficient for his purposes, and was worried that mathematical "fixes" would simply hide errors rather than remove them.
Von Neumann judged hardware random number generators unsuitable, for, if they did not record the output generated, they could not later be tested for errors. If they did record their output, they would exhaust the limited computer memories available then, and so the computer's ability to read and write numbers. If the numbers were written to cards, they would take very much longer to write and read. On the ENIAC
ENIAC
ENIAC was the first general-purpose electronic computer. It was a Turing-complete digital computer capable of being reprogrammed to solve a full range of computing problems....
computer he was using, the "middle square" method generated numbers at a rate some hundred times faster than reading numbers in from punched card
Punched card
A punched card, punch card, IBM card, or Hollerith card is a piece of stiff paper that contains digital information represented by the presence or absence of holes in predefined positions...
s.
The middle-square method has since been supplanted by more elaborate generators.
Mersenne Twister
The 1997 invention of the Mersenne Twister algorithm, by Makoto Matsumoto and Takuji Nishimura, avoids many of the problems with earlier generators. It has the colossal period of 219937−1 iterations (>4.3), is proven to be equidistributed in (up to) 623 dimensions (for 32-bit values), and runs faster than other statistically reasonable generators. It is now increasingly becoming the random number generator of choice for statistical simulations and generative modeling.SFMT, SIMD-oriented Fast Mersenne Twister, a variant of Mersenne Twister, is faster even if it's not compiled with SIMD
SIMD
Single instruction, multiple data , is a class of parallel computers in Flynn's taxonomy. It describes computers with multiple processing elements that perform the same operation on multiple data simultaneously...
support.http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/SFMT/speed.html
The native Mersenne Twister is not considered suitable for use in all cryptographic
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
applications. A variant of Mersenne Twister has been proposed as a cryptographic cipher. http://eprint.iacr.org/2005/165.pdf
Cryptographically secure pseudorandom number generators
A PRNG suitable for cryptographicCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
applications is called a cryptographically secure PRNG (CSPRNG). A requirement for a CSPRNG is that an adversary not knowing the seed has only negligible advantage
Advantage (cryptography)
In cryptography, an adversary's advantage is a measure of how successfully it can attack a cryptographic algorithm, by distinguishing it from an idealized version of that type of algorithm. Note that in this context, the "adversary" is itself an algorithm and not a person...
in distinguishing the generator's output sequence from a random sequence. In other words, while a PRNG is only required to pass certain statistical tests, a CSPRNG must pass all statistical tests that are restricted to polynomial time in the size of the seed. Though such property cannot be proven, strong evidence may be provided by reducing the CSPRNG to a problem
Mathematical problem
A mathematical problem is a problem that is amenable to being represented, analyzed, and possibly solved, with the methods of mathematics. This can be a real-world problem, such as computing the orbits of the planets in the solar system, or a problem of a more abstract nature, such as Hilbert's...
that is assumed to be hard, such as integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
. In general, years of review may be required before an algorithm can be certified as a CSPRNG.
Some classes of CSPRNGs include the following:
- Stream cipherStream cipherIn cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
s - Block cipherBlock cipherIn cryptography, a block cipher is a symmetric key cipher operating on fixed-length groups of bits, called blocks, with an unvarying transformation. A block cipher encryption algorithm might take a 128-bit block of plaintext as input, and output a corresponding 128-bit block of ciphertext...
s running in counter or output feedback mode. - PRNGs that have been designed specifically to be cryptographically secure, such as MicrosoftMicrosoftMicrosoft Corporation is an American public multinational corporation headquartered in Redmond, Washington, USA that develops, manufactures, licenses, and supports a wide range of products and services predominantly related to computing through its various product divisions...
's Cryptographic Application Programming InterfaceCryptographic Application Programming InterfaceThe Cryptographic Application Programming Interface is an application programming interface included with Microsoft Windows operating systems that provides services to enable developers to secure Windows-based applications using cryptography...
function CryptGenRandomCryptGenRandomCryptGenRandom is a cryptographically secure pseudorandom number generator function that is included in Microsoft's Cryptographic Application Programming Interface. In Win32 programs, Microsoft recommends its use anywhere random number generation is needed...
, the Yarrow algorithmYarrow algorithmThe Yarrow algorithm is a cryptographically secure pseudorandom number generator. The name is taken from the yarrow plant, the stalks of which are dried and used as a randomising agent in I Ching divination....
(incorporated in Mac OS XMac OS XMac OS X is a series of Unix-based operating systems and graphical user interfaces developed, marketed, and sold by Apple Inc. Since 2002, has been included with all new Macintosh computer systems...
and FreeBSDFreeBSDFreeBSD is a free Unix-like operating system descended from AT&T UNIX via BSD UNIX. Although for legal reasons FreeBSD cannot be called “UNIX”, as the direct descendant of BSD UNIX , FreeBSD’s internals and system APIs are UNIX-compliant...
), and FortunaFortuna (PRNG)Fortuna is a cryptographically secure pseudorandom number generator devised by Bruce Schneier and Niels Ferguson. It is named after Fortuna, the Roman goddess of chance.- Design :Fortuna is a family of secure PRNGs; its design...
. - Combination PRNGs which attempt to combine several PRNG primitive algorithms with the goal of removing any non-randomness.
- Special designs based on mathematical hardness assumptions. Examples include Micali-Schnorr and the Blum Blum Shub algorithm, which provide a strong security proof. Such algorithms are rather slow compared to traditional constructions, and impractical for many applications.
BSI evaluation criteria
The German Federal Office for Information SecurityFederal Office for Information Security
The Bundesamt für Sicherheit in der Informationstechnik is the German government agency in charge of managing computer and communication security for the German government...
(BSI) has established four criteria for quality of deterministic random number generators. They are summarized here:
- K1 — A sequence of random numbers with a low probability of containing identical consecutive elements.
- K2 — A sequence of numbers which is indistinguishable from 'true random' numbers according to specified statistical tests. The tests are the monobit test (equal numbers of ones and zeros in the sequence), poker test (a special instance of the chi-squared test), runs test (counts the frequency of runs of various lengths), longruns test (checks whether there exists any run of length 34 or greater in 20 000 bits of the sequence) — both from BSI2 (AIS 20, v. 1, 1999) and FIPS (140-1, 1994), and the autocorrelation test. In essence, these requirements are a test of how well a bit sequence: has zeros and ones equally often; after a sequence of n zeros (or ones), the next bit a one (or zero) with probability one-half; and any selected subsequence contains no information about the next element(s) in the sequence.
- K3 — It should be impossible for any attacker (for all practical purposes) to calculate, or otherwise guess, from any given sub-sequence, any previous or future values in the sequence, nor any inner state of the generator.
- K4 — It should be impossible, for all practical purposes, for an attacker to calculate, or guess from an inner state of the generator, any previous numbers in the sequence or any previous inner generator states.
For cryptographic applications, only generators meeting the K3 or K4 standard are acceptable.
Non-uniform generators
Numbers selected from a non-uniform probability distribution can be generated using a uniform distributionUniform distribution
-Probability theory:* Discrete uniform distribution* Continuous uniform distribution-Other:* "Uniform distribution modulo 1", see Equidistributed sequence*Uniform distribution , a type of species distribution* Distribution of military uniforms...
PRNG and a function that relates the two distributions.
First, one needs the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
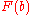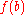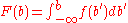
of the target distribution :Note that
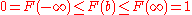. Using a random number c from a uniform distribution as the probability density to "pass by", we get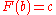so that
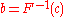
is a number randomly selected from distribution
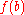.For example, the inverse of cumulative Gaussian distribution
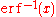with an ideal uniform PRNG with range (0, 1) as input would produce a sequence of (positive only) values with a Gaussian distribution; however
- when using practical number representations the infinite "tails" of the distribution have to be truncated to finite values.
- Repetitive recalculation of
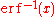should be reduced by means such as ziggurat algorithmZiggurat algorithmThe ziggurat algorithm is an algorithm for pseudo-random number sampling. Belonging to the class of rejection sampling algorithms, it relies on an underlying source of uniformly-distributed random numbers, typically from a pseudo-random number generator, as well as precomputed tables. The...
for faster generation.
Similar considerations apply to generating other non-uniform distributions such as Rayleigh and Poisson
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
.
See also
- List of pseudorandom number generators
- Pseudorandom binary sequence
- Quasi-random
- Random number generator attackRandom number generator attackThe security of cryptographic systems depends on some secret data that is known to authorized persons but unknown and unpredictable to others. To achieve this unpredictability, some randomization is typically employed...
- RandomnessRandomnessRandomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
External links
- Short video on random number generators explaining random seeds and middle squares method
- The GNU Scientific Library. A free (GPLGNU General Public LicenseThe GNU General Public License is the most widely used free software license, originally written by Richard Stallman for the GNU Project....
) CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
library that includes a number of PRNG algorithms. - Tina's Random Number Generator Library. A free (BSD licenseBSD licensesBSD licenses are a family of permissive free software licenses. The original license was used for the Berkeley Software Distribution , a Unix-like operating system after which it is named....
) state of the art C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
pseudo-random number generator library for sequential and parallel Monte Carlo simulations. - DieHarder: A free (GPLGNU General Public LicenseThe GNU General Public License is the most widely used free software license, originally written by Richard Stallman for the GNU Project....
) CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
Random Number Test Suite. - Research Randomizer A free browserWeb browserA web browser is a software application for retrieving, presenting, and traversing information resources on the World Wide Web. An information resource is identified by a Uniform Resource Identifier and may be a web page, image, video, or other piece of content...
-based PRNG which uses Java'sJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
"Math.random" method to generate numbers for random assignment and random sampling. - crng: Random-number generators (RNGs) implemented as Python extension types coded in C.
- http://eeyore.wu-wien.ac.at/src/ prng: A collection of algorithms for generating pseudorandom numbers as a library of C functions, released under the GPL
- Strange Attractors and TCP/IP Sequence Number Analysis - an analysis of the strength of PRNGs used to create TCP/IP sequence numbers by various operating systemOperating systemAn operating system is a set of programs that manage computer hardware resources and provide common services for application software. The operating system is the most important type of system software in a computer system...
s using strange attractors. This is a good practical example of issues in PRNGs and the variation possible in their implementation.- Strange Attractors and TCP/IP Sequence Number Analysis - One Year Later - a follow-up article demonstrating some of the evolution of various PRNG algorithms over time.
- Generating random numbers Generating random numbers in Embedded Systems by Eric Uner
- Analysis of the Linux Random Number Generator by Zvi Gutterman, Benny Pinkas, and Tzachy Reinman
- Functionality Classes and Evaluation Methodology for Deterministic Random Number Generators by Priv.-Doz. Dr. Werner Schindler, Federal Office for Information Security