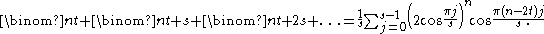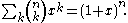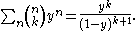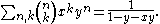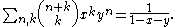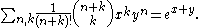Binomial coefficient
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, binomial coefficients are a family of positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s that occur as coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s in the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written
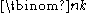 , and it is the coefficient
, and it is the coefficientCoefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
of the x k term in the polynomial expansion
Polynomial expansion
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition...
of the binomial
Binomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
(1 + x) n. Arranging binomial coefficients into rows for successive values of n, and in which k ranges from 0 to n, gives a triangular array called Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
.
This family of numbers also arises in many other areas than algebra, notably in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
. For any set containing n elements, the number of distinct k-element subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of it that can be formed (the k-combination
Combination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
s of its elements) is given by the binomial coefficient
 . Therefore
. Therefore 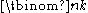 is often read as "n choose k". The properties of binomial coefficients have led to extending the meaning of the symbol
is often read as "n choose k". The properties of binomial coefficients have led to extending the meaning of the symbol 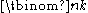 beyond the basic case where n and k are nonnegative integers with ; such expressions are then still called binomial coefficients.
beyond the basic case where n and k are nonnegative integers with ; such expressions are then still called binomial coefficients.The notation
 was introduced by Andreas von Ettingshausen
was introduced by Andreas von EttingshausenAndreas von Ettingshausen
Andreas Freiherr von Ettingshausen was a German mathematician and physicist.Ettingshausen studied philosophy and jurisprudence in Vienna. In 1817, he joined the University of Vienna and taught mathematics and physics...
in 1826, although the numbers were already known centuries before that (see Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
). The earliest known detailed discussion of binomial coefficients is in a tenth-century commentary, due to Halayudha
Halayudha
Halayudha was a 10th century Indian mathematician who wrote the ', a commentary on Pingala's Chandah-shastra, containing a clear description of Pascal's triangle ....
, on an ancient Hindu
Hindu
Hindu refers to an identity associated with the philosophical, religious and cultural systems that are indigenous to the Indian subcontinent. As used in the Constitution of India, the word "Hindu" is also attributed to all persons professing any Indian religion...
classic, Pingala
Pingala
Pingala is the traditional name of the author of the ' , the earliest known Sanskrit treatise on prosody.Nothing is known about Piṅgala himself...
's chandaḥśāstra. In about 1150, the Hindu mathematician Bhaskaracharya gave a very clear exposition of binomial coefficients in his book Lilavati
Lilavati
Lilavati was Indian mathematician Bhāskara II's treatise on mathematics. It is the first volume of his main work Siddhānta Shiromani, Sanskrit for "Crown of treatises," alongside Bijaganita, Grahaganita and Golādhyāya.- Name :The name comes from his daughter Līlāvatī...
.
Alternative notations include C(n, k), nCk, nCk,
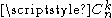 ,
, 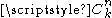 , in all of which the C stands for combination
, in all of which the C stands for combinationCombination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
s or choices.
Definition and interpretations
For natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (taken to include 0) n and k, the binomial coefficient
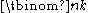 can be defined as the coefficient
can be defined as the coefficientCoefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
of the monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
Xk in the expansion of . The same coefficient also occurs (if ) in the binomial formula
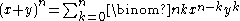
(valid for any elements x,y of a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
),
which explains the name "binomial coefficient".
Another occurrence of this number is in combinatorics, where it gives the number of ways, disregarding order, that k objects can be chosen from among n objects; more formally, the number of k-element subsets (or k-combination
Combination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
s) of an n-element set. This number can be seen as equal to the one of the first definition, independently of any of the formulas below to compute it: if in each of the n factors of the power one temporarily labels the term X with an index i (running from 1 to n), then each subset of k indices gives after expansion a contribution Xk, and the coefficient of that monomial in the result will be the number of such subsets. This shows in particular that
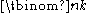 is a natural number for any natural numbers n and k. There are many other combinatorial interpretations of binomial coefficients (counting problems for which the answer is given by a binomial coefficient expression), for instance the number of words formed of n bit
is a natural number for any natural numbers n and k. There are many other combinatorial interpretations of binomial coefficients (counting problems for which the answer is given by a binomial coefficient expression), for instance the number of words formed of n bitBit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s (digits 0 or 1) whose sum is k is given by
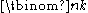 , while the number of ways to write
, while the number of ways to write 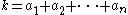 where every ai is a nonnegative integer is given by
where every ai is a nonnegative integer is given by 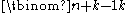 . Most of these interpretations are easily seen to be equivalent to counting k-combinations.
. Most of these interpretations are easily seen to be equivalent to counting k-combinations.Computing the value of binomial coefficients
Several methods exist to compute the value of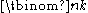 without actually expanding a binomial power or counting k-combinations.
without actually expanding a binomial power or counting k-combinations.Recursive formula
One has a recursiveRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
formula for binomial coefficients
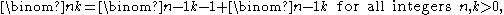
with initial values
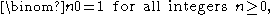
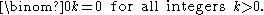
The formula follows either from tracing the contributions to Xk in , or by counting k-combinations of } that contain n and that do not contain n separately.
It follows easily that
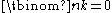 when k > n, and
when k > n, and 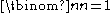 for all n, so the recursion can stop when reaching such cases. This recursive formula then allows the construction of Pascal's triangle
for all n, so the recursion can stop when reaching such cases. This recursive formula then allows the construction of Pascal's trianglePascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
.
Multiplicative formula
A more efficient method to compute individual binomial coefficients is given by the formula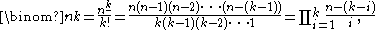
where the numerator of the first fraction is expressed as a falling factorial power.
This formula is easiest to understand for the combinatorial interpretation of binomial coefficients.
The numerator gives the number of ways to select a sequence of k distinct objects, retaining the order of selection, from a set of n objects. The denominator counts the number of distinct sequences that define the same k-combination when order is disregarded.
Factorial formula
Finally there is a formula using factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s that is easy to remember:
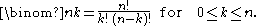
where n! denotes the factorial of n. This formula follows from the multiplicative formula above by multiplying numerator and denominator by ; as a consequence it involves many factors common to numerator and denominator. It is less practical for explicit computation unless common factors are first canceled (in particular since factorial values grow very rapidly). The formula does exhibit a symmetry that is less evident from the multiplicative formula (though it is from the definitions)
Generalization and connection to the binomial series
The multiplicative formula allows the definition of binomial coefficients to be extended by replacing n by an arbitrary number α (negative, real, complex) or even an element of any commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
in which all positive integers are invertible:

With this definition one has a generalization of the binomial formula (with one of the variables set to 1), which justifies still calling the
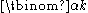 binomial coefficients:
binomial coefficients:This formula is valid for all complex numbers α and X with |X| < 1. It can also be interpreted as an identity of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
in X, where it actually can serve as definition of arbitrary powers of series with constant coefficient equal to 1; the point is that with this definition all identities hold that one expects for exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
, notably

If α is a nonnegative integer n, then all terms with k > n are zero, and the infinite series becomes a finite sum, thereby recovering the binomial formula. However for other values of α, including negative integers and rational numbers, the series is really infinite.
Pascal's triangle
Pascal's rule is the important recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
which can be used to prove by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
that
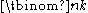 is a natural number for all n and k, (equivalent to the statement that k! divides the product of k consecutive integers), a fact that is not immediately obvious from formula (1).
is a natural number for all n and k, (equivalent to the statement that k! divides the product of k consecutive integers), a fact that is not immediately obvious from formula (1).Pascal's rule also gives rise to Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
:
| 0: | 1 | ||||||||||||||||
| 1: | 1 | 1 | |||||||||||||||
| 2: | 1 | 2 | 1 | ||||||||||||||
| 3: | 1 | 3 | 3 | 1 | |||||||||||||
| 4: | 1 | 4 | 6 | 4 | 1 | ||||||||||||
| 5: | 1 | 5 | 10 | 10 | 5 | 1 | |||||||||||
| 6: | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||
| 7: | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||
| 8: | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Row number n contains the numbers
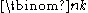 for k = 0,…,n. It is constructed by starting with ones at the outside and then always adding two adjacent numbers and writing the sum directly underneath. This method allows the quick calculation of binomial coefficients without the need for fractions or multiplications. For instance, by looking at row number 5 of the triangle, one can quickly read off that5 = 1 x5 + 5 x4y + 10 x3y2 + 10 x2y3 + 5 x y4 + 1 y5.
for k = 0,…,n. It is constructed by starting with ones at the outside and then always adding two adjacent numbers and writing the sum directly underneath. This method allows the quick calculation of binomial coefficients without the need for fractions or multiplications. For instance, by looking at row number 5 of the triangle, one can quickly read off that5 = 1 x5 + 5 x4y + 10 x3y2 + 10 x2y3 + 5 x y4 + 1 y5.The differences between elements on other diagonals are the elements in the previous diagonal, as a consequence of the recurrence relation above.
Combinatorics and statistics
Binomial coefficients are of importance in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, because they provide ready formulas for certain frequent counting problems:
- There are
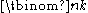 ways to choose k elements from a set of n elements. See CombinationCombinationIn mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
ways to choose k elements from a set of n elements. See CombinationCombinationIn mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
. - There are
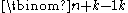 ways to choose k elements from a set of n if repetitions are allowed. See MultisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
ways to choose k elements from a set of n if repetitions are allowed. See MultisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
. - There are
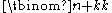 stringsString (computer science)In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
stringsString (computer science)In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
containing k ones and n zeros. - There are
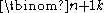 strings consisting of k ones and n zeros such that no two ones are adjacent.
strings consisting of k ones and n zeros such that no two ones are adjacent. - The Catalan numberCatalan numberIn combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
s are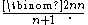
- The binomial distribution in statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
is
- The formula for a Bézier curveBézier curveA Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
.
Binomial coefficients as polynomials
For any nonnegative integer k, the expression can be simplified and defined as a polynomial divided by k!:
can be simplified and defined as a polynomial divided by k!: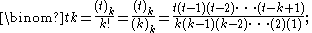
This presents a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in t with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
coefficients.
As such, it can be evaluated at any real or complex number t to define binomial coefficients with such first arguments.
These "generalized binomial coefficients" appear in Newton's generalized binomial theorem.
For each k, the polynomial
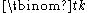 can be characterized as the unique degree k polynomial p(t) satisfying p(0) = p(1) = ... = p(k − 1) = 0 and p(k) = 1.
can be characterized as the unique degree k polynomial p(t) satisfying p(0) = p(1) = ... = p(k − 1) = 0 and p(k) = 1.Its coefficients are expressible in terms of Stirling numbers of the first kind
Stirling numbers of the first kind
In mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be...
, by definition of the latter:
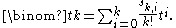
The derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of
 can be calculated by logarithmic differentiation:
can be calculated by logarithmic differentiation:
Binomial coefficients as a basis for the space of polynomials
Over any field containing QRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, each polynomial p(t) of degree at most d is uniquely expressible as a linear combination
 .
.The coefficient ak is the kth difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
of the sequence p(0), p(1), …, p(k).
Explicitly,
Integer-valued polynomials
Each polynomial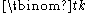 is integer-valued: it takes integer values at integer inputs.
is integer-valued: it takes integer values at integer inputs.(One way to prove this is by induction on k, using Pascal's identity.)
Therefore any integer linear combination of binomial coefficient polynomials is integer-valued too.
Conversely, shows that any integer-valued polynomial is an integer linear combination of these binomial coefficient polynomials.
More generally, for any subring R of a characteristic 0 field K, a polynomial in K[t] takes values in R at all integers if and only if it is an R-linear combination of binomial coefficient polynomials.
Example
The integer-valued polynomial 3t(3t + 1)/2 can be rewritten as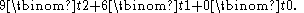
Identities involving binomial coefficients
The factorial formula facilitates relating nearby binomial coefficients. For instance, if k is a positive integer and n is arbitrary, then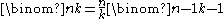
and, with a little more work,
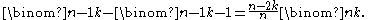
Moreover, the following may be useful:
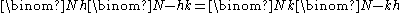
Series involving binomial coefficients
The formulais obtained from using x = 1. This is equivalent to saying that the elements in one row of Pascal's triangle always add up to two raised to an integer power. A combinatorial interpretation of this fact involving double counting
Double counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
is given by counting subsets of size 0, size 1, size 2, and so on up to size n of a set S of n elements. Since we count the number of subsets of size i for 0 ≤ i ≤ n, this sum must be equal to the number of subsets of S, which is known to be 2n. That is, Equation 5 is a statement that the power set for a finite set with n elements has size 2n.
More explicitly, consider a bit string with n digits. This bit string can be used to represent 2n numbers. Now consider all of the bit strings with no ones in them. There is just one, or rather n choose 0. Next consider the number of bit strings with just a single one in them. There are n, or rather n choose 1. Continuing this way we can see that the equation above holds.
The formulas
and
follow from , after differentiating
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
with respect to x (twice in the latter) and then substituting x = 1.
The Chu-Vandermonde identity, which holds for any complex-values m and n and any non-negative integer k, is
and can be found by examination of the coefficient of
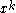 in the expansion of (1 + x)m (1 + x)n − m = (1 + x)n using equation . When m = 1, equation reduces to equation .
in the expansion of (1 + x)m (1 + x)n − m = (1 + x)n using equation . When m = 1, equation reduces to equation .A similar looking formula, which applies for any integers j, k, and n satisfying 0 ≤ j ≤ k ≤ n, is
and can be found by examination of the coefficient of
 in the expansion of
in the expansion of 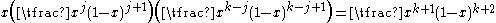
using
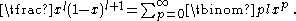
When j = k, equation gives
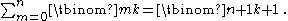
From expansion using n = 2m, k = m, and , one finds
Let F(n) denote the n-th Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
.
We obtain a formula about the diagonals of Pascal's triangle
This can be proved by induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
using or by Zeckendorf's representation
Zeckendorf's theorem
Zeckendorf's theorem, named after Belgian mathematician Edouard Zeckendorf, is a theorem about the representation of integers as sums of Fibonacci numbers....
(Just note that the lhs gives the number of subsets of {F(2),...,F(n)} without consecutive members, which also form all the numbers below F(n+1)).
Also using and induction, one can show that
Although there is no closed formula for

(unless one resorts to Hypergeometric functions), one can again use and induction, to show that for k = 0, ..., n−1
as well as
which is itself a special case of the result from the theory of finite differences that for any polynomial P(x) of degree less than n,
Differentiating k times and setting x = −1 yields this for
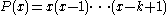 ,
,when 0 ≤ k < n,
and the general case follows by taking linear combinations of these.
When P(x) is of degree less than or equal to n,
where
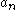 is the coefficient of degree n in P(x).
is the coefficient of degree n in P(x).More generally for ,
where m and d are complex numbers. This follows immediately applying to the polynomial Q(x):=P(m + dx) instead of P(x), and observing that Q(x) has still degree less than or equal to n, and that its coefficient of degree n is dnan.
The infinite series
is convergent for k ≥ 2. This formula is used in the analysis of the German tank problem
German tank problem
In the statistical theory of estimation, estimating the maximum of a uniform distribution is a common illustration of differences between estimation methods...
.
It is equivalent to the formula for the finite sum
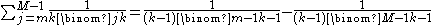
which is proved for M>m by induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
on M.
Using one can derive
and
Series multisection
Series multisection
In mathematics, a multisection of a power series is a new power series composed of equally-spaced terms extracted unaltered from the original. Formally, if one is giventhen a multisection is a power series of the form...
gives the following identity for the sum of binomial coefficients taken with a step s and offset t
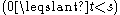 as a closed-form sum of s terms:
as a closed-form sum of s terms:
Identities with combinatorial proofs
Many identities involving binomial coefficients can be proved by combinatorial meansCombinatorial proof
In mathematics, the term combinatorial proof is often used to mean either of two types of proof of an identity in enumerative combinatorics that either states that two sets of combinatorial configurations, depending on one or more parameters, have the same number of elements , or gives a formula...
. For example, the following identity for nonnegative integers
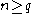 (which reduces to (6) when
(which reduces to (6) when 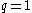 ):
):can be given a double counting proof
Double counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
as follows. The left side counts the number of ways of selecting a subset of
 of at least q elements, and marking q elements among those selected. The right side counts the same parameter, because there are
of at least q elements, and marking q elements among those selected. The right side counts the same parameter, because there are 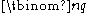 ways of choosing a set of q marks and they occur in all subsets that additionally contain some subset of the remaining elements, of which there are
ways of choosing a set of q marks and they occur in all subsets that additionally contain some subset of the remaining elements, of which there are 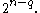
The recursion formula
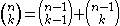
where both sides count the number of k-element subsets of {1, 2, . . ., n} with the right hand side first grouping them into those that contain element n and those that do not.
The identity also has a combinatorial proof. The identity reads
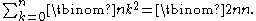
Suppose you have
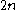 empty squares arranged in a row and you want to mark (select) n of them. There are
empty squares arranged in a row and you want to mark (select) n of them. There are 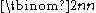 ways to do this. On the other hand, you may select your n squares by selecting k squares from among the first n and
ways to do this. On the other hand, you may select your n squares by selecting k squares from among the first n and  squares from the remaining n squares; any k from 1 to n will work. This gives
squares from the remaining n squares; any k from 1 to n will work. This gives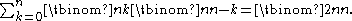
Now apply (4) to get the result.
Sum of coefficients row
The number of k-combinations for all k,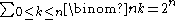 , is the sum of the nth row (counting from 0) of the binomial coefficients. These combinations are enumerated by the 1 digits of the set of base 2 numbers counting from 0 to
, is the sum of the nth row (counting from 0) of the binomial coefficients. These combinations are enumerated by the 1 digits of the set of base 2 numbers counting from 0 to 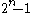 , where each digit position is an item from the set of n.
, where each digit position is an item from the set of n.Dixon's identity
Dixon's identityDixon's identity
In mathematics, Dixon's identity is any of several different but closely related identities proved by A. C. Dixon, some involving finite sums of products of three binomial coefficients, and some evaluating a hypergeometric sum...
is
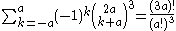
or, more generally,
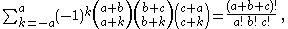
where a, b, and c are non-negative integers.
Continuous identities
Certain trigonometric integrals have values expressible in terms ofbinomial coefficients:
For
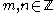 and
and 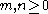
These can be proved by using Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
to convert trigonometric functions to complex exponentials, expanding using the binomial theorem, and integrating term by term.
Ordinary generating functions
For a fixed n, the ordinary generating function of the sequence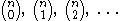 is:
is:
For a fixed k, the ordinary generating function of the sequence
 is:
is:
The bivariate generating function of the binomial coefficients is:
Another bivariate generating function of the binomial coefficients, which is symmetric, is:
Exponential generating function
The exponential bivariate generating function of the binomial coefficients is:Divisibility properties
In 1852, KummerErnst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
proved that if m and n are nonnegative integers and p is a prime number, then the largest power of p dividing
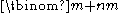 equals pc, where c is the number of carries when m and n are added in base p.
equals pc, where c is the number of carries when m and n are added in base p.Equivalently, the exponent of a prime p in
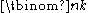
equals the number of nonnegative integers j such that the fractional part
Fractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
of k/pj is greater than the fractional part of n/pj. It can be deduced from this that
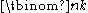 is divisible by n/gcd
is divisible by n/gcdGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(n,k).
A somewhat surprising result by David Singmaster
David Singmaster
David Breyer Singmaster is a retired professor of mathematics at London South Bank University, England, UK. A self-described metagrobologist, he is most famous for his solution to the Rubik's cube and his huge personal collection of mechanical puzzles and books of brain teasers. He is also...
(1974) is that any integer divides almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
binomial coefficients. More precisely, fix an integer d and let f(N) denote the number of binomial coefficients
 with n < N such that d divides
with n < N such that d divides 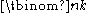 . Then
. Then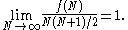
Since the number of binomial coefficients
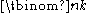 with n < N is N(N+1) / 2, this implies that the density of binomial coefficients divisible by d goes to 1.
with n < N is N(N+1) / 2, this implies that the density of binomial coefficients divisible by d goes to 1.Another fact:
An integer n ≥ 2 is prime if and only if
all the intermediate binomial coefficients
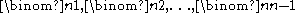
are divisible by n.
Proof:
When p is prime, p divides
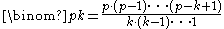 for all 0 < k < p
for all 0 < k < pbecause it is a natural number and the numerator has a prime factor p but the denominator does not have a prime factor p.
When n is composite, let p be the smallest prime factor of n and let k = n/p. Then 0 < p < n and
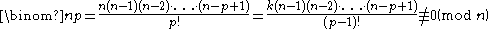
otherwise the numerator k(n−1)(n−2)×...×(n−p+1) has to be divisible by n = k×p, this can only be the case when (n−1)(n−2)×...×(n−p+1) is divisible by p. But n is divisible by p, so p does not divide n−1, n−2, ..., n−p+1 and because p is prime, we know that p does not divide (n−1)(n−2)×...×(n−p+1) and so the numerator cannot be divisible by n.
Bounds and asymptotic formulas
The following bounds for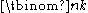 hold:
hold: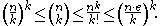
Stirling's approximation
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
yields the bounds:
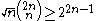 and, in general,
and, in general,  for m ≥ 2 and n ≥ 1,
for m ≥ 2 and n ≥ 1,and the approximation
-
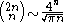 as
as 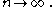
The infinite product formula (cf. Gamma function, alternative definition)
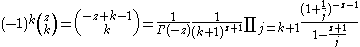
yields the asymptotic formulas
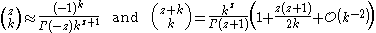
as
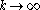 .
.This asymptotic behaviour is contained in the approximation
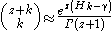
as well. (Here
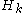 is the k-th harmonic number and
is the k-th harmonic number and 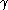 is the Euler–Mascheroni constant
is the Euler–Mascheroni constantEuler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
).
The sum of binomial coefficients can be bounded by a term exponential in
 and the binary entropy of the largest
and the binary entropy of the largest 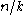 that occurs. More precisely, for
that occurs. More precisely, for 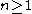 and
and 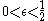 , it holds
, it holds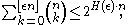
where
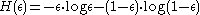 is the binary entropy of
is the binary entropy of  .
.A simple and rough upper bound for the sum of binomial coefficients is given by the formula below (not difficult to prove)
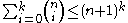
Generalization to multinomials
Binomial coefficients can be generalized to multinomial coefficients.They are defined to be the number:
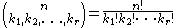
where
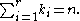
While the binomial coefficients represent the coefficients of (x+y)n, the multinomial coefficients
represent the coefficients of the polynomial
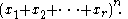
See multinomial theorem
Multinomial theorem
In mathematics, the multinomial theorem says how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem to polynomials.-Theorem:...
. The case r = 2 gives binomial coefficients:
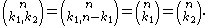
The combinatorial interpretation of multinomial coefficients is distribution of n distinguishable elements over r (distinguishable) containers, each containing exactly ki elements, where i is the index of the container.
Multinomial coefficients have many properties similar to these of binomial coefficients, for example the recurrence relation:
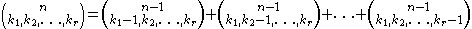
and symmetry:
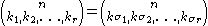
where
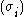 is a permutation
is a permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of (1,2,...,r).
Generalization to negative integers
If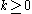 , then
, then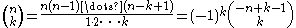 extends to all
extends to all  .
.In the special case
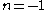 , this reduces to
, this reduces to 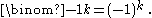
Taylor series
Using Stirling numbers of the first kindStirling numbers of the first kind
In mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be...
the series expansion
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
around any arbitrarily chosen point
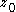 is
is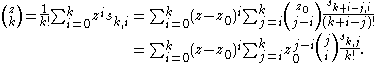
Binomial coefficient with n=1/2
The definition of the binomial coefficients can be extended to the case where is real and
is real and 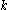 is integer.
is integer.In particular, the following identity holds for any non-negative integer
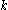 :
: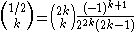
This shows up when expanding
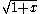 into a power series using the Newton binomial series :
into a power series using the Newton binomial series :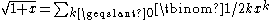
Identity for the product of binomial coefficients
One can express the product of binomial coefficients as a linear combination of binomial coefficients: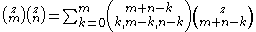
where the connection coefficients are multinomial coefficients
Multinomial theorem
In mathematics, the multinomial theorem says how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem to polynomials.-Theorem:...
. In terms of labelled combinatorial objects, the connection coefficients represent the number of ways to assign m+n-k labels to a pair of labelled combinatorial objects—of weight m and n respectively—that have had their first k labels identified, or glued together to get a new labelled combinatorial object of weight m+n-k. (That is, to separate the labels into three portions to apply to the glued part, the unglued part of the first object, and the unglued part of the second object.) In this regard, binomial coefficients are to exponential generating series what falling factorials are to ordinary generating series.
Partial Fraction Decomposition
The partial fraction decomposition of the inverse is given by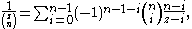 and
and 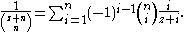
Newton's binomial series
Newton's binomial seriesBinomial series
In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
, named after Sir Isaac Newton, is one of the simplest Newton series:
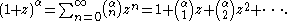
The identity can be obtained by showing that both sides satisfy the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
(1+z) f(z) = α f(z).
The radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of this series is 1. An alternative expression is
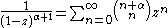
where the identity
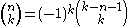
is applied.
Two real or complex valued arguments
The binomial coefficient is generalized to two real or complex valued arguments using the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
or beta function via
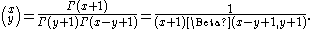
This definition inherits these following additional properties from
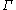 :
: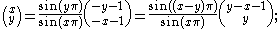
moreover,
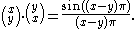
The resulting function has been little-studied, apparently first being graphed in . Notably, many binomial identities fail:
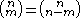 but
but 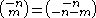 for n positive (so
for n positive (so  negative). The behavior is quite complex, and markedly different in various octants (that is, with respect to the x and y axes and the line
negative). The behavior is quite complex, and markedly different in various octants (that is, with respect to the x and y axes and the line 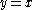 ), with the behavior for negative x having singularities at negative integer values and a checkerboard of positive and negative regions:
), with the behavior for negative x having singularities at negative integer values and a checkerboard of positive and negative regions:
- in the octant
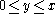 it is a smoothly interpolated form of the usual binomial, with a ridge ("Pascal's ridge").
it is a smoothly interpolated form of the usual binomial, with a ridge ("Pascal's ridge"). - in the octant
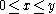 and in the quadrant
and in the quadrant 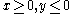 the function is close to zero.
the function is close to zero. - in the quadrant
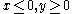 the function is alternatingly very large positive and negative on the parallelograms with vertices
the function is alternatingly very large positive and negative on the parallelograms with vertices 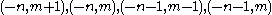
- in the octant
 the behavior is again alternatingly very large positive and negative, but on a square grid.
the behavior is again alternatingly very large positive and negative, but on a square grid. - in the octant
 it is close to zero, except for near the singularities.
it is close to zero, except for near the singularities.
Generalization to q-series
The binomial coefficient has a q-analogQ-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
generalization known as the Gaussian binomial coefficient.
Generalization to infinite cardinals
The definition of the binomial coefficient can be generalized to infinite cardinalsCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
by defining:
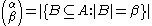
where A is some set with cardinality
 . One can show that the generalized binomial coefficient is well-defined, in the sense that no matter what set we choose to represent the cardinal number
. One can show that the generalized binomial coefficient is well-defined, in the sense that no matter what set we choose to represent the cardinal number  ,
, 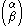 will remain the same. For finite cardinals, this definition coincides with the standard definition of the binomial coefficient.
will remain the same. For finite cardinals, this definition coincides with the standard definition of the binomial coefficient.Assuming the Axiom of Choice, one can show that
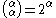 for any infinite cardinal
for any infinite cardinal  .
.Binomial coefficient in programming languages
The notation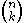 is convenient in handwriting but inconvenient for typewriter
is convenient in handwriting but inconvenient for typewriterTypewriter
A typewriter is a mechanical or electromechanical device with keys that, when pressed, cause characters to be printed on a medium, usually paper. Typically one character is printed per keypress, and the machine prints the characters by making ink impressions of type elements similar to the pieces...
s and computer terminal
Computer terminal
A computer terminal is an electronic or electromechanical hardware device that is used for entering data into, and displaying data from, a computer or a computing system...
s. Many programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s do not offer a standard subroutine
Subroutine
In computer science, a subroutine is a portion of code within a larger program that performs a specific task and is relatively independent of the remaining code....
for computing the binomial coefficient, but for example the J programming language uses the exclamation mark: k ! n .
Naive implementations of the factorial formula, such as the following snippet in Python
Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
:
def binomialCoefficient(n, k):
from math import factorial
return factorial(n) // (factorial(k) * factorial(n - k))
are very slow and are uselessly calculating factorials of very high numbers (in languages as C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
or Java
Java (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
they suffer from overflow errors because of this reason). A direct implementation of the multiplicative formula works well:
def binomialCoefficient(n, k):
if k > n - k: # take advantage of symmetry
k = n - k
c = 1
for i in range(k):
c = c * (n - (k - i))
c = c // i
return c
The example mentioned above can be also written in functional style. The following Scheme example uses recursive definition
Rational arithmetic can be easily avoided using integer division
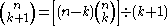
The following implementation uses all these ideas
(define (binomial n k)
- Helper function to compute C(n,k) via forward recursio
(define (binomial-iter n k i prev)
(if (>= i k)
prev
(binomial-iter n k (+ i 1) (/ (* (- n i) prev) (+ i 1)))))
- Use symmetry property C(n,k)=C(n, n-k
(if (< k (- n k))
(binomial-iter n k 0 1)
(binomial-iter n (- n k) 0 1)))
Another way to compute the binomial coefficient when using large numbers is to recognize that
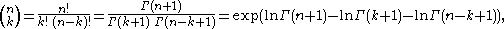
where
 denotes the natural logarithm
denotes the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
at
 . It is a special function that is easily computed and is standard in some programming languages such as using log_gamma in Maxima, LogGamma in Mathematica
. It is a special function that is easily computed and is standard in some programming languages such as using log_gamma in Maxima, LogGamma in MathematicaMathematica
Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
, or gammaln in MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
. Roundoff error may cause the returned value to not be an integer.
See also
- Central binomial coefficientCentral binomial coefficientIn mathematics the nth central binomial coefficient is defined in terms of the binomial coefficient byThey are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle...
- Binomial transform
- Star of David theoremStar of David theoremThe Star of David theorem is a mathematical result on arithmetic properties of binomial coefficients. It was discovered by H.W. Gould in 1972.- Statement :...
- Table of Newtonian series
- List of factorial and binomial topics
- Multiplicities of entries in Pascal's triangleMultiplicities of entries in Pascal's triangleIn combinatorial number theory, Singmaster's conjecture, named after David Singmaster, says there is a finite upper bound on the multiplicities of entries in Pascal's triangle...
- Sun's curious identity
- Kummer's theoremKummer's theoremIn mathematics, Kummer's theorem, named after Ernst Kummer, is as follows. Given integers n ≥ m ≥ 0 and a prime number p, the maximum integer k such that pk divides the binomial coefficient \binom n m is equal to the number of carries when m is added to n − m...
on prime-power divisors of binomial coefficients