Combination
Encyclopedia
In mathematics
a combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruit, say an apple, orange and pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange.
More formally a k-combination of a set S is a subset of k distinct elements of S. If the set has n elements the number of k-combinations is equal to the binomial coefficient
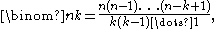
which can be written using factorial
s as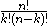
whenever 
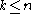, and which is zero when 
.
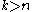The set of all k-combinations of a set S is sometimes denoted by
.
Combinations can consider the combination of n things taken k at a time without or with repetitions. In the above example repetitions were not allowed. If however it was possible to have two of any one kind of fruit there would be 3 more combinations: one with two apples, one with two oranges, and one with two pears.
With large sets, it becomes necessary to use mathematics to find the number of combinations. For example, a poker hand can be described as a 5-combination (k = 5) of cards from a 52 card deck (n = 52). The 5 cards of the hand are all distinct, and the order of cards in the hand does not matter. There are 2,598,960 such combinations, and the chance of drawing any one hand at random is 1 / 2,598,960.
, 
, 
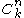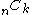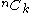or even 
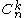(the latter form is standard in French, Russian, and Polish texts). The same number however occurs in many other mathematical contexts, where it is denoted by 
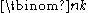; notably it occurs as coefficient in the binomial formula, hence its name binomial coefficient. One can define 
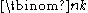for all natural numbers k at once by the relation
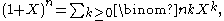
from which it is clear that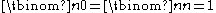
and 
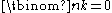for k > n. To see that these coefficients count k-combinations from S, one can first consider a collection of n distinct variables Xs labeled by the elements s of S, and expand the product
over all elements of S:
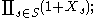
it has 2n distinct terms corresponding to all the subsets of S, each subset giving the product of the corresponding variables Xs. Now setting all of the Xs equal to the unlabeled variable X, so that the product becomes , the term for each k-combination from S becomes Xk, so that the coefficient of that power in the result equals the number of such k-combinations.
Binomial coefficients can be computed explicitly in various ways. To get all of them for the expansions up to , one can use (in addition to the basic cases already given) the recursion relation
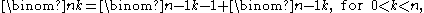
which follows from =; this leads to the construction of Pascal's triangle
.
For determining an individual binomial coefficient, it is more practical to use the formula
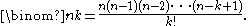
The numerator gives the number of k-permutations of n, i.e., of sequences of k distinct elements of S, while the denominator gives the number of such k-permutations that give the same k-combination when the order is ignored.
When k exceeds n/2, the above formula contains factors common to the numerator and the denominator, and canceling them out gives the relation
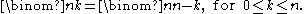
This expresses a symmetry that is evident from the binomial formula, and can also be understood in terms of k-combinations by taking the complement
of such a combination, which is an -combination.
Finally there is a formula which exhibits this symmetry directly, and has the merit of being easy to remember:
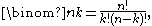
where n! denotes the factorial
of n. It is obtained from the previous formula by multiplying denominator and numerator by !, so it is certainly inferior as a method of computation to that formula.
The last formula can be understood directly, by considering the n! permutations of all the elements of S. Each such permutation gives a k-combination by selecting its first k elements. There are many duplicate selections: any combined permutation of the first k elements among each other, and of the final (n − k) elements among each other produces the same combination; this explains the division in the formula.
From the above formulas follow relations between adjacent numbers in Pascal's triangle in all three directions:
,
,
.
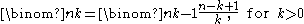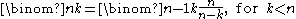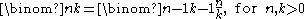Together with the basic cases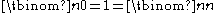
, these allow successive computation of respectively all numbers of combinations from the same set (a row in Pascal's triangle), of k-combinations of sets of growing sizes, and of combinations with a complement of fixed size .
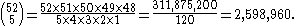
Alternatively one may use the formula in terms of factorials and cancel the factors in the numerator against parts of the factors in the denominator, after which only multiplication of the remaining factors is required: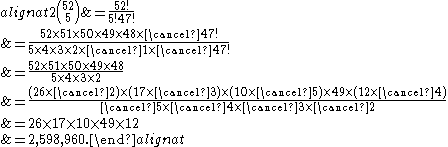
Another alternative computation, almost equivalent to the first, is based on writing
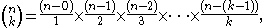
which gives
When evaluated as , this can be computed using only integer arithmetic. The reason that all divisions are without remainder is that the intermediate results they produce are themselves binomial coefficients.
Using the symmetric formula in terms of factorials without performing simplifications gives a rather extensive calculation:
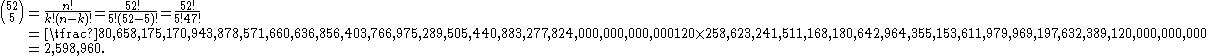
from an interval of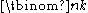
integers with the set of those k-combinations. Assuming is itself ordered, for instance }, there are two natural possibilities for ordering its k-combinations: by comparing their smallest elements first (as in the illustrations above) or by comparing their largest elements first. The latter option has the advantage that adding a new largest element to will not change the initial part of the enumeration, but just add the new k-combinations of the larger set after the previous ones. Repeating this process, the enumeration can be extended indefinitely with k-combinations of ever larger sets. If moreover the intervals of the integers are taken to start at 0, then the k-combination at a given place i in the enumeration can be computed easily from i, and the bijection so obtained is known as the combinatorial number system. It is also known as "rank"/"ranking" and "unranking" in computational mathematics.
, namely by
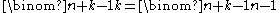
(the case where both n and k are zero is special; the correct value 1 (for the empty 0-multicombination) is given by left hand side
, but not by the right hand side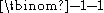 
).
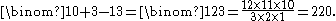
The analogy with the k-combination case can be stressed by writing the numerator as a rising power
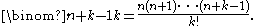
There is an easy way to understand the above result. Label the elements of S with numbers 0, 1, ..., , and choose a k-combination from the set of numbers { 1, 2, ..., } (so that there are unchosen numbers). Now change this k-combination into a k-multicombination of S by replacing every (chosen) number x in the k-combination by the element of S labeled by the number of unchosen numbers less than x. This is always a number in the range of the labels, and it is easy to see that every k-multicombination of S is obtained for one choice of a k-combination.
A concrete example may be helpful. Suppose there are 4 types of fruits (apple, orange, pear, banana) at a grocery store, and you want to buy 12 pieces of fruit. So n = 4 and k = 12. Use label 0 for apples, 1 for oranges, 2 for pears, and 3 for bananas. A selection of 12 fruits can be translated into a selection of 12 distinct numbers in the range 1,...,15 by selecting as many consecutive numbers starting from 1 as there are apples in the selection, then skip a number, continue choosing as many consecutive numbers as there are oranges selected, again skip a number, then again for pears, skip one again, and finally choose the remaining numbers (as many as there are bananas selected). For instance for 2 apples, 7 oranges, 0 pears and 3 bananas, the numbers chosen will be 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15. To recover the fruits, the numbers 1, 2 (not preceded by any unchosen numbers) are replaced by apples, the numbers 4, 5, ..., 10 (preceded by one unchosen number: 3) by oranges, and the numbers 13, 14, 15 (preceded by three unchosen numbers: 3, 11, and 12) by bananas; there are no chosen numbers preceded by exactly 2 unchosen numbers, and therefore no pears in the selection.
The total number of possible selections is
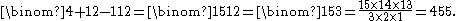
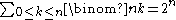, is the sum of the nth row (counting from 0) of the binomial coefficients. These combinations are enumerated by the 1 digits of the set of base 2 numbers counting from 0 to 
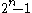, where each digit position is an item from the set of n.
is extremely slow for large sample sizes. One way to select a k-combination efficiently from a population of size n is to iterate across each element of the population, and at each step pick that element with a dynamically changing probability of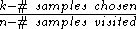
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruit, say an apple, orange and pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange.
More formally a k-combination of a set S is a subset of k distinct elements of S. If the set has n elements the number of k-combinations is equal to the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
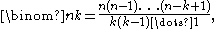
which can be written using factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s as
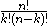whenever 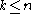, and which is zero when 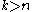.The set of all k-combinations of a set S is sometimes denoted by
.Combinations can consider the combination of n things taken k at a time without or with repetitions. In the above example repetitions were not allowed. If however it was possible to have two of any one kind of fruit there would be 3 more combinations: one with two apples, one with two oranges, and one with two pears.
With large sets, it becomes necessary to use mathematics to find the number of combinations. For example, a poker hand can be described as a 5-combination (k = 5) of cards from a 52 card deck (n = 52). The 5 cards of the hand are all distinct, and the order of cards in the hand does not matter. There are 2,598,960 such combinations, and the chance of drawing any one hand at random is 1 / 2,598,960.
Number of k-combinations
The number of k-combinations from a given set S of n elements is often denoted in elementary combinatorics texts by C(n, k), or by a variation such as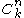, , 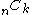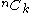or even 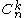(the latter form is standard in French, Russian, and Polish texts). The same number however occurs in many other mathematical contexts, where it is denoted by 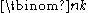; notably it occurs as coefficient in the binomial formula, hence its name binomial coefficient. One can define 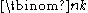for all natural numbers k at once by the relation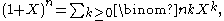from which it is clear that
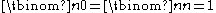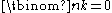and for k > n. To see that these coefficients count k-combinations from S, one can first consider a collection of n distinct variables Xs labeled by the elements s of S, and expand the productMultiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
over all elements of S:
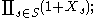
it has 2n distinct terms corresponding to all the subsets of S, each subset giving the product of the corresponding variables Xs. Now setting all of the Xs equal to the unlabeled variable X, so that the product becomes , the term for each k-combination from S becomes Xk, so that the coefficient of that power in the result equals the number of such k-combinations.
Binomial coefficients can be computed explicitly in various ways. To get all of them for the expansions up to , one can use (in addition to the basic cases already given) the recursion relation
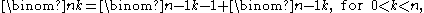
which follows from =; this leads to the construction of Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
.
For determining an individual binomial coefficient, it is more practical to use the formula
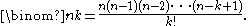
The numerator gives the number of k-permutations of n, i.e., of sequences of k distinct elements of S, while the denominator gives the number of such k-permutations that give the same k-combination when the order is ignored.
When k exceeds n/2, the above formula contains factors common to the numerator and the denominator, and canceling them out gives the relation
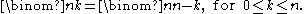
This expresses a symmetry that is evident from the binomial formula, and can also be understood in terms of k-combinations by taking the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of such a combination, which is an -combination.
Finally there is a formula which exhibits this symmetry directly, and has the merit of being easy to remember:
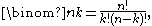
where n
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of n. It is obtained from the previous formula by multiplying denominator and numerator by !, so it is certainly inferior as a method of computation to that formula.
The last formula can be understood directly, by considering the n
From the above formulas follow relations between adjacent numbers in Pascal's triangle in all three directions:
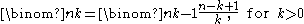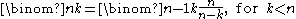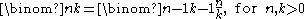,,.Together with the basic cases
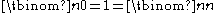, these allow successive computation of respectively all numbers of combinations from the same set (a row in Pascal's triangle), of k-combinations of sets of growing sizes, and of combinations with a complement of fixed size .Example of counting combinations
As a concrete example, one can compute the number of five-card hands possible from a standard fifty-two card deck as: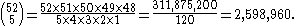Alternatively one may use the formula in terms of factorials and cancel the factors in the numerator against parts of the factors in the denominator, after which only multiplication of the remaining factors is required:
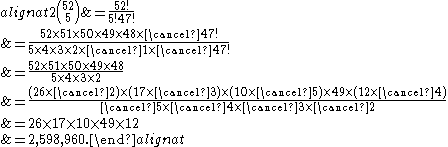
Another alternative computation, almost equivalent to the first, is based on writing
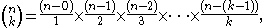
which gives
When evaluated as , this can be computed using only integer arithmetic. The reason that all divisions are without remainder is that the intermediate results they produce are themselves binomial coefficients.
Using the symmetric formula in terms of factorials without performing simplifications gives a rather extensive calculation:
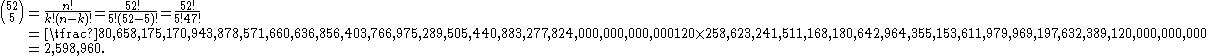
Enumerating k-combinations
One can enumerate all k-combinations of a given set of n elements in some fixed order, which establishes a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from an interval of
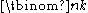integers with the set of those k-combinations. Assuming is itself ordered, for instance }, there are two natural possibilities for ordering its k-combinations: by comparing their smallest elements first (as in the illustrations above) or by comparing their largest elements first. The latter option has the advantage that adding a new largest element to will not change the initial part of the enumeration, but just add the new k-combinations of the larger set after the previous ones. Repeating this process, the enumeration can be extended indefinitely with k-combinations of ever larger sets. If moreover the intervals of the integers are taken to start at 0, then the k-combination at a given place i in the enumeration can be computed easily from i, and the bijection so obtained is known as the combinatorial number system. It is also known as "rank"/"ranking" and "unranking" in computational mathematics.Number of combinations with repetition
A k-combination with repetitions, or k-multicombination, or multiset of size k from a set S is given by a sequence of k not necessarily distinct elements of S, where order is not taken into account: two sequences of which one can be obtained from the other by permuting the terms define the same multiset. If S has n elements, the number of such k-multicombinations is also given by a binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
, namely by
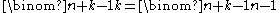
(the case where both n and k are zero is special; the correct value 1 (for the empty 0-multicombination) is given by left hand side
, but not by the right hand side 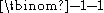).Example of counting multicombinations
For example, if you have ten types of donuts (n = 10) on a menu to choose from and you want three donuts (k = 3), the number of ways to choose can be calculated as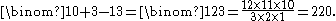The analogy with the k-combination case can be stressed by writing the numerator as a rising power
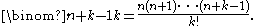
There is an easy way to understand the above result. Label the elements of S with numbers 0, 1, ..., , and choose a k-combination from the set of numbers { 1, 2, ..., } (so that there are unchosen numbers). Now change this k-combination into a k-multicombination of S by replacing every (chosen) number x in the k-combination by the element of S labeled by the number of unchosen numbers less than x. This is always a number in the range of the labels, and it is easy to see that every k-multicombination of S is obtained for one choice of a k-combination.
A concrete example may be helpful. Suppose there are 4 types of fruits (apple, orange, pear, banana) at a grocery store, and you want to buy 12 pieces of fruit. So n = 4 and k = 12. Use label 0 for apples, 1 for oranges, 2 for pears, and 3 for bananas. A selection of 12 fruits can be translated into a selection of 12 distinct numbers in the range 1,...,15 by selecting as many consecutive numbers starting from 1 as there are apples in the selection, then skip a number, continue choosing as many consecutive numbers as there are oranges selected, again skip a number, then again for pears, skip one again, and finally choose the remaining numbers (as many as there are bananas selected). For instance for 2 apples, 7 oranges, 0 pears and 3 bananas, the numbers chosen will be 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15. To recover the fruits, the numbers 1, 2 (not preceded by any unchosen numbers) are replaced by apples, the numbers 4, 5, ..., 10 (preceded by one unchosen number: 3) by oranges, and the numbers 13, 14, 15 (preceded by three unchosen numbers: 3, 11, and 12) by bananas; there are no chosen numbers preceded by exactly 2 unchosen numbers, and therefore no pears in the selection.
The total number of possible selections is
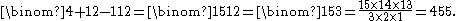
Number of k-combinations for all k
The number of k-combinations for all k,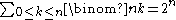, is the sum of the nth row (counting from 0) of the binomial coefficients. These combinations are enumerated by the 1 digits of the set of base 2 numbers counting from 0 to 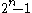, where each digit position is an item from the set of n.Probability: sampling a random combination
There are various algorithms to pick out a random combination from a given set or list. Rejection samplingRejection sampling
In mathematics, rejection sampling is a basic pseudo-random number sampling technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm"....
is extremely slow for large sample sizes. One way to select a k-combination efficiently from a population of size n is to iterate across each element of the population, and at each step pick that element with a dynamically changing probability of
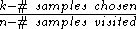.See also
- Combinatorial number system
- CombinatoricsCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
- MultisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
- Binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
- PermutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
- List of permutation topics
- SubsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
- ProbabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
- Pascal's TrianglePascal's triangleIn mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
External links
- C code to generate all combinations of n elements chosen as k
- Many Common types of permutation and combination math problems, with detailed solutions
- The Unknown Formula For combinations when choices can be repeated and order does NOT matter
- http://www.nitte.ac.in/userfiles/file/Combinations%20with%20Repetitions.pdf Combinations with repetitions (by: Akshatha AG and Smitha B)