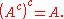In set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, a complement of a set A refers to things not in (that is, things outside of), A. The relative complement of A with respect to a set B, is the set of elements in B but not in A. When all sets under consideration are considered to be subsets of a given set U, the absolute complement of A is the set of all elements in U but not in A.
If A and B are sets, then the relative complement of A in B, also known as the set-theoretic difference of B and A, is the set of elements in B, but not in A.

The relative complement of A in B is denoted B ∖ A according to the ISO 31-11 standard (sometimes written B − A, but this notation is ambiguous, as in some contexts it can be interpreted as the set of all b − a, where b is taken from B and a from A).

Formally


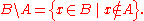
Examples:

• {1,2,3} ∖ {2,3,4}   =   {1}
• {2,3,4} ∖ {1,2,3}   =   {4}
• If is the set of real number
  Real number
  In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
  
  s and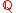 is the set of rational number
  Rational number
  In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
  
  s, then is the set of irrational number
  Irrational number
  In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
  
  s.

The following lists some notable properties of relative complements in relation to the set-theoretic operation

Operation (mathematics)

The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....

s of union

Union (set theory)

In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

 and intersection

Intersection (set theory)

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

.

If A, B, and C are sets, then the following identities

Identity (mathematics)

In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...

 hold:

• C ∖ (A ∩ B)  =  (C ∖ A)∪(C ∖ B)
• C ∖ (A ∪ B)  =  (C ∖ A)∩(C ∖ B)
• C ∖ (B ∖ A)  =  (A ∩ C)∪(C ∖ B)
• (B ∖ A) ∩ C  =  (B ∩ C) ∖ A  =  B∩(C ∖ A)
• (B ∖ A) ∪ C  =  (B ∪ C) ∖ (A ∖ C)
• A ∖ A  =  Ø
• Ø ∖ A  =  Ø
• A ∖ Ø  =  A

If a universe

Universe (mathematics)

In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...

 U is defined, then the relative complement of A in U is called the absolute complement (or simply complement) of A, and is denoted by A^c or sometimes A′, also the same set often is denoted by

Complement laws:

• 
• 
• 
• 
• 

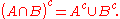
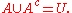
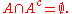
  (this follows from the equivalence of a conditional with its contrapositive)

Involution or double complement law:

• 

Relationships between relative and absolute complements:

• A ∖ B = A ∩ B^c
• (A ∖ B)^c = A^c ∪ B

The first two complement laws above shows that if A is a non-empty, proper subset of U, then {A, A^c} is a partition

Partition of a set

In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...

 of U.
In the LaTeX

LaTeX

LaTeX is a document markup language and document preparation system for the TeX typesetting program. Within the typesetting system, its name is styled as . The term LaTeX refers only to the language in which documents are written, not to the editor used to write those documents. In order to...

 typesetting language, the command \setminus is usually used for rendering a set difference symbol, which is similar to a backslash

Backslash

The backslash is a typographical mark used mainly in computing. It was first introduced to computers in 1960 by Bob Bemer. Sometimes called a reverse solidus or a slosh, it is the mirror image of the common slash....

 symbol.