Stirling numbers of the first kind
Encyclopedia
In mathematics
, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling number
s. They commonly occur in combinatorics
, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be understood to be inverses of one-another, when taken as triangular matrices
. This article is devoted to specifics of Stirling numbers of the first kind; further identities linking the two kinds, and general information, is given in the article on Stirling numbers.
s of n elements with k disjoint cycle
s.
The unsigned Stirling numbers arise as
coefficients of the rising factorial, i.e.,
.
Most identities on this page deal with the unsigned Stirling numbers.
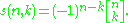
They are the coefficients in the expansion
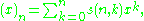
where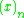
is the falling factorial
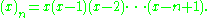
Note that
Warning: the notations for signed and unsigned Stirling numbers are sometimes defined just the other way round.
for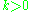
, with the initial conditions
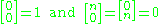
for n > 0.
The above follows from the recurrence relation on the rising factorials:
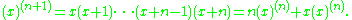
Below is a triangular array
of unsigned values for the Stirling numbers of the first kind, similar in form to Pascal's triangle
.
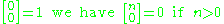
and
Also
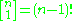
and
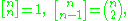
and
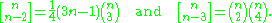
Similar relationships involving the Stirling numbers hold for the Bernoulli polynomials
. Many relations for the Stirling numbers shadow similar relations on the binomial coefficient
s. The study of these 'shadow relationships' is termed umbral calculus
and culminates in the theory of Sheffer sequences.
For example, how many permutations on [n] are there that consist of n − 3 cycles?
There are three possibilities:
We enumerate the three types, as follows:
Sum the three contributions to obtain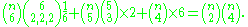
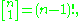
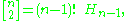
where Hn is a harmonic number, and
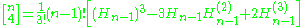
where Hn(m) is a generalized harmonic number. A generalization of this relation to harmonic numbers is given in a later section.
And we have also: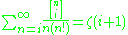
where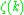
is the Riemann zeta function.
:
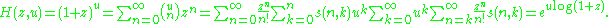
In particular, the order of summation may be exchanged, and derivatives taken, and then z or u may be fixed.
Similarly, we may derive:
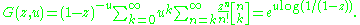
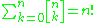
or in a more general relationship,
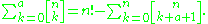
The identity
can be proved by the techniques on the page
Stirling numbers and exponential generating functions
.
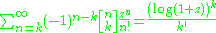
where |z| < 1 (the singularity nearest to z = 0 of log(1 + z) is at z = −1.)
where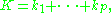
and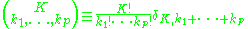
is a multinomial coefficient. The Kronecker delta in the first equation restricts the sums over the ks to a sum over the partitions
of p.
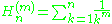
as follows:
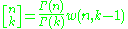
where w(n, 0) = 1 and
In the above,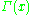
is the Gamma function
.
.svg.png)
The absolute value
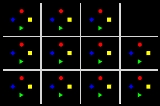
of the Stirling number of the first kind, s(n, k), counts the number of permutation
s of n objects with exactly k orbits (equivalently, with exactly k cycle
s). For example, s(4, 2) = 11, corresponds to the fact that the symmetric group
on 4 objects has 3 permutations of the form
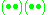—2 orbits of size 2 each
and 8 permutations of the form
—1 orbit of size 3, and 1 orbit of size 1
(see the entry on cycle notation
for the meaning of the above expressions.)
Let us prove this. First, we can remark that the unsigned Stirling numbers of the first kind are characterized by the following recurrence relation:
To see why the above recurrence relation matches the count of permutations with k cycles, consider forming a permutation of n + 1 objects from a permutation of n objects by adding a distinguished object. There are exactly two ways in which this can be accomplished. We could do this by forming a singleton cycle, i.e. leaving the extra object alone. This accounts for the s(n, k − 1) term in the recurrence formula. We could also insert the new object into one of the existing cycles. Consider an arbitrary permutation of n objects with k cycles, and label the objects a1, ..., an, so that the permutation is represented by
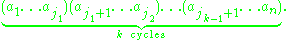
To form a new permutation of n + 1 objects and k cycles one must insert the new object into this array. There are, evidently n ways to perform this insertion. This explains the n s(n, k) term of the recurrence relation. Q.E.D.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling number
Stirling number
In mathematics, Stirling numbers arise in a variety of combinatorics problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second...
s. They commonly occur in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be understood to be inverses of one-another, when taken as triangular matrices
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
. This article is devoted to specifics of Stirling numbers of the first kind; further identities linking the two kinds, and general information, is given in the article on Stirling numbers.
Unsigned Stirling numbers of the first kind
The unsigned Stirling numbers of the first kind count the number of permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of n elements with k disjoint cycle
Cyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
s.
The unsigned Stirling numbers arise as
coefficients of the rising factorial, i.e.,
.Most identities on this page deal with the unsigned Stirling numbers.
Stirling numbers of the first kind
Stirling numbers of the first kind (often without the qualifying adjective signed) are given by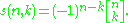They are the coefficients in the expansion
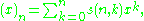
where
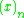is the falling factorial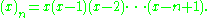Note that
Warning: the notations for signed and unsigned Stirling numbers are sometimes defined just the other way round.
Recurrence relation and table of values for the unsigned Stirling numbers
The unsigned Stirling numbers of the first kind can be calculated by the recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
for
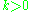, with the initial conditions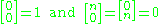for n > 0.
The above follows from the recurrence relation on the rising factorials:
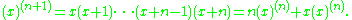
Below is a triangular array
Triangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index.Notable particular examples include these:...
of unsigned values for the Stirling numbers of the first kind, similar in form to Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
.
| n \ k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | |||||||||
| 1 | 0 | 1 | ||||||||
| 2 | 0 | 1 | 1 | |||||||
| 3 | 0 | 2 | 3 | 1 | ||||||
| 4 | 0 | 6 | 11 | 6 | 1 | |||||
| 5 | 0 | 24 | 50 | 35 | 10 | 1 | ||||
| 6 | 0 | 120 | 274 | 225 | 85 | 15 | 1 | |||
| 7 | 0 | 720 | 1764 | 1624 | 735 | 175 | 21 | 1 | ||
| 8 | 0 | 5040 | 13068 | 13132 | 6769 | 1960 | 322 | 28 | 1 | |
| 9 | 0 | 40320 | 109584 | 118124 | 67284 | 22449 | 4536 | 546 | 36 | 1 |
Simple identities
Note that although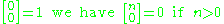and
Also
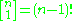
and
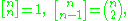
and
Similar relationships involving the Stirling numbers hold for the Bernoulli polynomials
Bernoulli polynomials
In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
. Many relations for the Stirling numbers shadow similar relations on the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s. The study of these 'shadow relationships' is termed umbral calculus
Umbral calculus
In mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
and culminates in the theory of Sheffer sequences.
Combinatorial proofs
These identities may be derived by enumerating permutations directly.For example, how many permutations on [n] are there that consist of n − 3 cycles?
There are three possibilities:
- n − 6 fixed points and three two-cycles
- n − 5 fixed points, a three-cycle and a two-cycle, and
- n − 4 fixed points and a four-cycle.
We enumerate the three types, as follows:
- choose the six elements that go into the two-cycles, decompose them into two-cycles and take into account that the order of the cycles is not important:
-
- choose the five elements that go into the three-cycle and the two-cycle, choose the elements of the three-cycle and take into account that three elements generate two three-cycles:
- choose the four elements of the four-cycle and take into account that four elements generate six four-cycles:
Sum the three contributions to obtain
Other relations
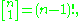
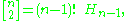
These includewhere Hn is a harmonic number, and
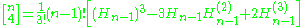
where Hn(m) is a generalized harmonic number. A generalization of this relation to harmonic numbers is given in a later section.
And we have also:
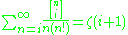
where
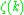is the Riemann zeta function.Generating function
A variety of identities may be derived by manipulating the generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
:
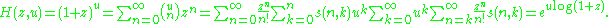
In particular, the order of summation may be exchanged, and derivatives taken, and then z or u may be fixed.
Similarly, we may derive:
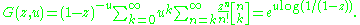
Finite sums
A simple sum is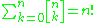or in a more general relationship,
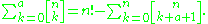
The identity
can be proved by the techniques on the page
Stirling numbers and exponential generating functions
Stirling numbers and exponential generating functions
The use of exponential generating functions to study the properties of Stirling numbers is a classical exercise in combinatorics and possibly the canonical example of how symbolic combinatorics, the method that encapsulates the fundamental theorem of combinatorial enumeration, is used...
.
Infinite sums
Some infinite sums include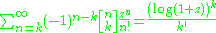where |z| < 1 (the singularity nearest to z = 0 of log(1 + z) is at z = −1.)
Explicit formula
The Stirling number s(n,n-p) can be found from the formulawhere
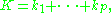
and
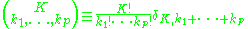
is a multinomial coefficient. The Kronecker delta in the first equation restricts the sums over the ks to a sum over the partitions
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of p.
Relation to harmonic numbers
Stirling numbers of the first kind can be expressed in terms of the harmonic numbers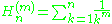as follows:
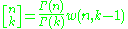
where w(n, 0) = 1 and
In the above,
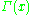is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
Enumerative interpretation
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the Stirling number of the first kind, s(n, k), counts the number of permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of n objects with exactly k orbits (equivalently, with exactly k cycle
Cyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
s). For example, s(4, 2) = 11, corresponds to the fact that the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 4 objects has 3 permutations of the form
—2 orbits of size 2 eachand 8 permutations of the form
—1 orbit of size 3, and 1 orbit of size 1(see the entry on cycle notation
Cycle notation
In combinatorial mathematics, the cycle notation is a useful convention for writing down a permutation in terms of its constituent cycles. This is also called circular notation and the permutation called a cyclic or circular permutation....
for the meaning of the above expressions.)
Let us prove this. First, we can remark that the unsigned Stirling numbers of the first kind are characterized by the following recurrence relation:
To see why the above recurrence relation matches the count of permutations with k cycles, consider forming a permutation of n + 1 objects from a permutation of n objects by adding a distinguished object. There are exactly two ways in which this can be accomplished. We could do this by forming a singleton cycle, i.e. leaving the extra object alone. This accounts for the s(n, k − 1) term in the recurrence formula. We could also insert the new object into one of the existing cycles. Consider an arbitrary permutation of n objects with k cycles, and label the objects a1, ..., an, so that the permutation is represented by
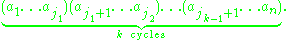
To form a new permutation of n + 1 objects and k cycles one must insert the new object into this array. There are, evidently n ways to perform this insertion. This explains the n s(n, k) term of the recurrence relation. Q.E.D.