Umbral calculus
Encyclopedia
In mathematics
before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method. They are often attributed to Édouard Lucas
(or James Joseph Sylvester
), who used the technique extensively.
In the 1930s and 1940s, Eric Temple Bell
attempted to set the umbral calculus on a rigorous footing.
In the 1970s, Steven Roman
, Gian-Carlo Rota
, and others developed the umbral calculus by means of linear functional
s on spaces of polynomials. Currently, umbral calculus refers to the study of Sheffer sequences, including polynomial sequences of binomial type and Appell sequences.
. Consider, for example, the ordinary binomial expansion
and the remarkably similar-looking relation on the Bernoulli polynomials
:
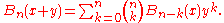
Compare also the ordinary derivative
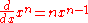
to a very similar-looking relation on the Bernoulli polynomials:
These similarities allow one to construct umbral proofs, which, on the surface cannot be correct, but seem to work anyway. Thus, for example, by pretending that the subscript n − k is an exponent:
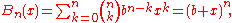
and then differentiating, one gets the desired result:
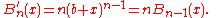
In the above, the variable b is an "umbra" (Latin
for shadow).
See also Faulhaber's formula.
is given by a similar expression involving the k 'th forward differences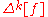
of a polynomial
function f,
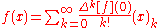
where
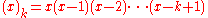
is the Pochhammer symbol
used here for the falling sequential product. A similar relationship holds for the backward differences and rising factorial.
This series is also known as the Newton series or Newton's forward difference expansion.
The analogy to Taylor's expansion is utilized in the Calculus of finite differences.
tried unsuccessfully to make this kind of argument logically rigorous. The combinatorialist
John Riordan
in his book Combinatorial Identities published in the 1960s, used techniques of this sort extensively.
, pointed out that the mystery vanishes if one considers the linear functional
L on polynomials in y defined by
Then one can write
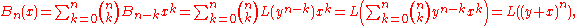
etc. Rota later stated that much confusion resulted from the failure to distinguish between three equivalence relation
s that occur frequently in this topic, all of which were denoted by "=".
In a paper published in 1964, Rota used umbral methods to establish the recursion
formula satisfied by the Bell numbers, which enumerate partitions
of finite sets.
In the paper of Roman and Rota cited below, the umbral calculus is characterized as the study of the umbral algebra, defined as the algebra
of linear functionals on the vector space
of polynomials in a variable x, with a product L1L2 of linear functionals defined by
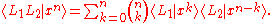
When polynomial sequence
s replace sequences of numbers as images of yn under the linear mapping L, then the umbral method is seen to be an essential component of Rota's general theory of special polynomials, and that theory is the umbral calculus by some more modern definitions of the term. A small sample of that theory can be found in the article on polynomial sequences of binomial type. Another is the article titled Sheffer sequence.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method. They are often attributed to Édouard Lucas
Edouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
(or James Joseph Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
), who used the technique extensively.
In the 1930s and 1940s, Eric Temple Bell
Eric Temple Bell
Eric Temple Bell , was a mathematician and science fiction author born in Scotland who lived in the U.S. for most of his life...
attempted to set the umbral calculus on a rigorous footing.
In the 1970s, Steven Roman
Steven Roman
Steven Roman is a mathematician, currently Emeritus Professor of Mathematics at California State University and Lecturer in Mathematics at University of California. He is one of the main developers of umbral calculus. He has written around 40 books on mathematics and computer programming.-External...
, Gian-Carlo Rota
Gian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
, and others developed the umbral calculus by means of linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s on spaces of polynomials. Currently, umbral calculus refers to the study of Sheffer sequences, including polynomial sequences of binomial type and Appell sequences.
The 19th-century umbral calculus
That method is a notational device for deriving identities involving indexed sequences of numbers by pretending that the indices are exponents. Construed literally, it is absurd, and yet it is successful; identities derived via the umbral calculus can also be derived by more complicated methods that can be taken literally without logical difficulty. An example involves the Bernoulli polynomialsBernoulli polynomials
In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
. Consider, for example, the ordinary binomial expansion
and the remarkably similar-looking relation on the Bernoulli polynomials
Bernoulli polynomials
In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
:
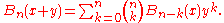
Compare also the ordinary derivative
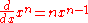
to a very similar-looking relation on the Bernoulli polynomials:
These similarities allow one to construct umbral proofs, which, on the surface cannot be correct, but seem to work anyway. Thus, for example, by pretending that the subscript n − k is an exponent:
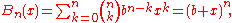
and then differentiating, one gets the desired result:
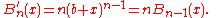
In the above, the variable b is an "umbra" (Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
for shadow).
See also Faulhaber's formula.
Umbral Taylor series
Similar relationships were also observed in the theory of finite differences. The umbral version of the Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
is given by a similar expression involving the k 'th forward differences
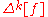of a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function f,
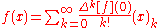
where
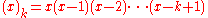
is the Pochhammer symbol
Pochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
used here for the falling sequential product. A similar relationship holds for the backward differences and rising factorial.
This series is also known as the Newton series or Newton's forward difference expansion.
The analogy to Taylor's expansion is utilized in the Calculus of finite differences.
Bell and Riordan
In the 1930s and 1940s, Eric Temple BellEric Temple Bell
Eric Temple Bell , was a mathematician and science fiction author born in Scotland who lived in the U.S. for most of his life...
tried unsuccessfully to make this kind of argument logically rigorous. The combinatorialist
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
John Riordan
John Riordan
John Riordan was an American mathematician and the author of major early works in combinatorics, particularly Introduction to Combinatorial Analysis and Combinatorial Identities.- Life :...
in his book Combinatorial Identities published in the 1960s, used techniques of this sort extensively.
The modern umbral calculus
Another combinatorialist, Gian-Carlo RotaGian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
, pointed out that the mystery vanishes if one considers the linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
L on polynomials in y defined by
Then one can write
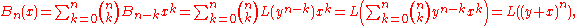
etc. Rota later stated that much confusion resulted from the failure to distinguish between three equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s that occur frequently in this topic, all of which were denoted by "=".
In a paper published in 1964, Rota used umbral methods to establish the recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
formula satisfied by the Bell numbers, which enumerate partitions
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of finite sets.
In the paper of Roman and Rota cited below, the umbral calculus is characterized as the study of the umbral algebra, defined as the algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of linear functionals on the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of polynomials in a variable x, with a product L1L2 of linear functionals defined by
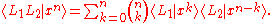
When polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
s replace sequences of numbers as images of yn under the linear mapping L, then the umbral method is seen to be an essential component of Rota's general theory of special polynomials, and that theory is the umbral calculus by some more modern definitions of the term. A small sample of that theory can be found in the article on polynomial sequences of binomial type. Another is the article titled Sheffer sequence.