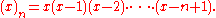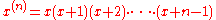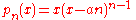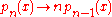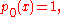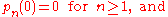Binomial type
Encyclopedia
In mathematics
, a polynomial sequence
, i.e., a sequence of polynomial
s indexed by { 0, 1, 2, 3, ... } in which the index of each polynomial equals its degree, is said to be of binomial type if it satisfies the sequence of identities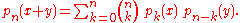
Many such sequences exist. The set of all such sequences forms a Lie group
under the operation of umbral composition, explained below. Every sequence of binomial type may be expressed in terms of the Bell polynomials. Every sequence of binomial type is a Sheffer sequence (but most Sheffer sequences are not of binomial type). Polynomial sequences put on firm footing the vague 19th century notions of umbral calculus
.
The product is understood to be 1 if n = 0, since it is in that case an empty product
. This polynomial sequence is of binomial type.
(The statement that this operator is shift-equivariant is the same as saying that the polynomial sequence is a Sheffer sequence; the set of sequences of binomial type is properly included within the set of Sheffer sequences.)
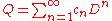
where D is differentiation (note that the lower bound of summation is 1). Each delta operator Q has a unique sequence of "basic polynomials", i.e., a polynomial sequence satisfying
It was shown in 1973 by Rota
, Kahaner, and Odlyzko
, that a polynomial sequence is of binomial type if and only if it is the sequence of basic polynomials of some delta operator. Therefore, this paragraph amounts to a recipe for generating as many polynomial sequences of binomial type as one may wish.
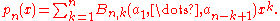
Where Bn,k(a1, ..., an−k+1) is the Bell polynomial. Then this polynomial sequence is of binomial type. Note that for each n ≥ 1,
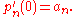
Here is the main result of this section:
Theorem: All polynomial sequences of binomial type are of this form.
A result in Mullin and Rota, repeated in Rota, Kahaner, and Odlyzko (see References below) states that every polynomial sequence { pn(x) }n of binomial type is determined by the sequence { pn′(0) }n, but those sources do not mention Bell polynomials.
This sequence of scalars is also related to the delta operator. Let
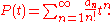
Then
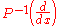
is the delta operator of this sequence.
by
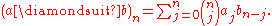
Let
be the nth term of the sequence
Then for any sequence ai, i = 0, 1, 2, ..., with a0 = 0, the sequence defined by p0(x) = 1 and
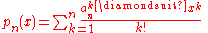
for n ≥ 1, is of binomial type, and every sequence of binomial type is of this form. This result is due to Alessandro di Bucchianico (see References below).
s are formal (not necessarily convergent) power series of the form
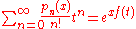
where f(t) is a formal power series whose constant term
is zero and whose first-degree term is not zero. It can be shown by the use of the power-series version of Faà di Bruno's formula
that
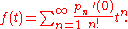
The delta operator of the sequence is f−1(D), so that
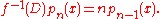
and
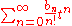
are
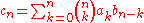
(see also Cauchy product). If we think of x as a parameter indexing a family of such power series, then the binomial identity says in effect that the power series indexed by x + y is the product of those indexed by x and by y. Thus the x is the argument to a function that maps sums to products: an exponential function
where f(t) has the form given above.
in which the group operation is "umbral composition" of polynomial sequences. That operation is defined as follows. Suppose { pn(x) : n = 0, 1, 2, 3, ... } and { qn(x) : n = 0, 1, 2, 3, ... } are polynomial sequences, and
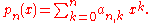
Then the umbral composition p o q is the polynomial sequence whose nth term is
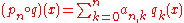
(the subscript n appears in pn, since this is the n term of that sequence, but not in q, since this refers to the sequence as a whole rather than one of its terms).
With the delta operator defined by a power series in D as above, the natural bijection between delta operators and polynomial sequences of binomial type, also defined above, is a group isomorphism, in which the group operation on power series is formal composition of formal power series.
s of the polynomial sequence. It can be shown that the whole polynomial sequence of binomial type is determined by its cumulants, in a way discussed in the article titled cumulant
. Thus
the nth cumulant
and
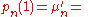the nth moment.
These are "formal" cumulants and "formal" moments
, as opposed to cumulants of a probability distribution
and moments of a probability distribution.
Let
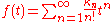
be the (formal) cumulant-generating function. Then
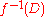
is the delta operator associated with the polynomial sequence, i.e., we have
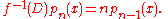
, probability
, statistics
, and a variety of other fields.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
, i.e., a sequence of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s indexed by { 0, 1, 2, 3, ... } in which the index of each polynomial equals its degree, is said to be of binomial type if it satisfies the sequence of identities
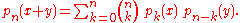
Many such sequences exist. The set of all such sequences forms a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
under the operation of umbral composition, explained below. Every sequence of binomial type may be expressed in terms of the Bell polynomials. Every sequence of binomial type is a Sheffer sequence (but most Sheffer sequences are not of binomial type). Polynomial sequences put on firm footing the vague 19th century notions of umbral calculus
Umbral calculus
In mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
.
Examples
- In consequence of this definition the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
can be stated by saying that the sequence { xn : n = 0, 1, 2, ... } is of binomial type.
- The sequence of "lower factorials" is defined by
The product is understood to be 1 if n = 0, since it is in that case an empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
. This polynomial sequence is of binomial type.
- Similarly the "upper factorials"
- are a polynomial sequence of binomial type.
- The Abel polynomials
- are a polynomial sequence of binomial type.
- where S(n, k) is the number of partitions of a set of size n into k disjoint non-empty subsets, is a polynomial sequence of binomial type. Eric Temple BellEric Temple BellEric Temple Bell , was a mathematician and science fiction author born in Scotland who lived in the U.S. for most of his life...
called these the "exponential polynomials" and that term is also sometimes seen in the literature. The coefficients S(n, k ) are "Stirling numberStirling numberIn mathematics, Stirling numbers arise in a variety of combinatorics problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second...
s of the second kind". This sequence has a curious connection with the Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
: If X is a random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with a Poisson distribution with expected value λ then E(Xn) = pn(λ). In particular, when λ = 1, we see that the nth moment of the Poisson distribution with expected value 1 is the number of partitions of a set of size n, called the nth Bell number. This fact about the nth moment of that particular Poisson distribution is "Dobinski's formula".
Characterization by delta operators
It can be shown that a polynomial sequence { pn(x) : n = 0, 1, 2, ... } is of binomial type if and only if all three of the following conditions hold:- The linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
on the space of polynomials in x that is characterized by
- is shift-equivariant, and
- p0(x) = 1 for all x, and
- pn(0) = 0 for n > 0.
(The statement that this operator is shift-equivariant is the same as saying that the polynomial sequence is a Sheffer sequence; the set of sequences of binomial type is properly included within the set of Sheffer sequences.)
Delta operators
That linear transformation is clearly a delta operator, i.e., a shift-equivariant linear transformation on the space of polynomials in x that reduces degrees of polynomials by 1. The most obvious examples of delta operators are difference operators and differentiation. It can be shown that every delta operator can be written as a power series of the form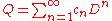where D is differentiation (note that the lower bound of summation is 1). Each delta operator Q has a unique sequence of "basic polynomials", i.e., a polynomial sequence satisfying
It was shown in 1973 by Rota
Gian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
, Kahaner, and Odlyzko
Andrew Odlyzko
Andrew Michael Odlyzko is a mathematician and a former head of the University of Minnesota's Digital Technology Center.In the field of mathematics he has published extensively on analytic number theory, computational number theory, cryptography, algorithms and computational complexity,...
, that a polynomial sequence is of binomial type if and only if it is the sequence of basic polynomials of some delta operator. Therefore, this paragraph amounts to a recipe for generating as many polynomial sequences of binomial type as one may wish.
Characterization by Bell polynomials
For any sequence a1, a2, a3, ... of scalars, let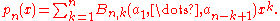Where Bn,k(a1, ..., an−k+1) is the Bell polynomial. Then this polynomial sequence is of binomial type. Note that for each n ≥ 1,
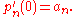
Here is the main result of this section:
Theorem: All polynomial sequences of binomial type are of this form.
A result in Mullin and Rota, repeated in Rota, Kahaner, and Odlyzko (see References below) states that every polynomial sequence { pn(x) }n of binomial type is determined by the sequence { pn′(0) }n, but those sources do not mention Bell polynomials.
This sequence of scalars is also related to the delta operator. Let
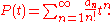
Then
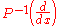
is the delta operator of this sequence.
Characterization by a convolution identity
For sequences an, bn, n = 0, 1, 2, ..., define a sort of convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
by
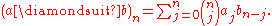
Let
be the nth term of the sequenceThen for any sequence ai, i = 0, 1, 2, ..., with a0 = 0, the sequence defined by p0(x) = 1 and
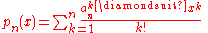
for n ≥ 1, is of binomial type, and every sequence of binomial type is of this form. This result is due to Alessandro di Bucchianico (see References below).
Characterization by generating functions
Polynomial sequences of binomial type are precisely those whose generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s are formal (not necessarily convergent) power series of the form
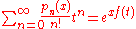
where f(t) is a formal power series whose constant term
Constant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
is zero and whose first-degree term is not zero. It can be shown by the use of the power-series version of Faà di Bruno's formula
Faà di Bruno's formula
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula...
that
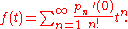
The delta operator of the sequence is f−1(D), so that
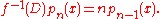
A way to think about these generating functions
The coefficients in the product of two formal power seriesand
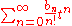
are
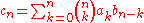
(see also Cauchy product). If we think of x as a parameter indexing a family of such power series, then the binomial identity says in effect that the power series indexed by x + y is the product of those indexed by x and by y. Thus the x is the argument to a function that maps sums to products: an exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
where f(t) has the form given above.
Umbral composition of polynomial sequences
The set of all polynomial sequences of binomial type is a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
in which the group operation is "umbral composition" of polynomial sequences. That operation is defined as follows. Suppose { pn(x) : n = 0, 1, 2, 3, ... } and { qn(x) : n = 0, 1, 2, 3, ... } are polynomial sequences, and
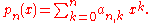
Then the umbral composition p o q is the polynomial sequence whose nth term is
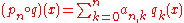
(the subscript n appears in pn, since this is the n term of that sequence, but not in q, since this refers to the sequence as a whole rather than one of its terms).
With the delta operator defined by a power series in D as above, the natural bijection between delta operators and polynomial sequences of binomial type, also defined above, is a group isomorphism, in which the group operation on power series is formal composition of formal power series.
Cumulants and moments
The sequence κn of coefficients of the first-degree terms in a polynomial sequence of binomial type may be termed the cumulantCumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s of the polynomial sequence. It can be shown that the whole polynomial sequence of binomial type is determined by its cumulants, in a way discussed in the article titled cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
. Thus
the nth cumulantand
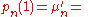the nth moment.These are "formal" cumulants and "formal" moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
, as opposed to cumulants of a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
and moments of a probability distribution.
Let
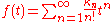
be the (formal) cumulant-generating function. Then
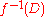
is the delta operator associated with the polynomial sequence, i.e., we have
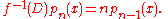
Applications
The concept of binomial type has applications in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, and a variety of other fields.
See also
- List of factorial and binomial topics
- Binomial-QMFBinomial-QMFOrthonormal binomial quadrature mirror filter bank with perfect reconstruction was designed by Ali Akansu, et al. published in 1990 using the family of binomial polynomials for subband decomposition of discrete-time signals....
(Daubechies wavelet filters)