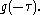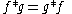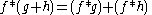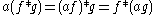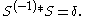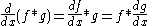Convolution
Encyclopedia
In mathematics
and, in particular, functional analysis
, convolution is a mathematical operation
on two function
s f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation
. It has applications that include probability
, statistics
, computer vision
, image
and signal processing
, electrical engineering
, and differential equations.
The convolution can be defined for functions on groups
other than Euclidean space
. In particular, the circular convolution
can be defined for periodic function
s (that is, functions on the circle
), and the discrete convolution can be defined for functions on the set of integers. These generalizations of the convolution have applications in the field of numerical analysis
and numerical linear algebra
, and in the design and implementation of finite impulse response
filters in signal processing.
Computing the inverse of the convolution operation is known as deconvolution
.
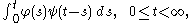
is a particular case of composition products considered by the Italian mathematician Vito Volterra
in 1913.
Convolution is also sometimes called "Faltung" (which means folding in German
); both Faltung and convolution were used as early as 1903, though the definition is rather unfamiliar in older uses.
The term Faltung was sometimes used in English through the 1940s, before the notion of convolution became widely used, along with other terms such as composition product, superposition integral, and Carson's integral.
or star. It is defined as the integral of the product of the two functions after one is reversed and shifted. As such, it is a particular kind of integral transform:
While the symbol t is used above, it need not represent the time domain. But in that context, the convolution formula can be described as a weighted average of the function ƒ(τ) at the moment t where the weighting is given by g(−τ) simply shifted by amount t. As t changes, the weighting function emphasizes different parts of the input function.
More generally, if f and g are complex-valued functions on Rd, then their convolution may be defined as the integral:

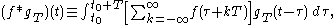
where to is an arbitrary choice. The summation is called a periodic summation of the function ƒ.
If gT is a periodic summation of another function, g, then ƒ∗gT is known as a circular, cyclic, or periodic convolution of ƒ and g.
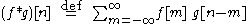
When multiplying two polynomial
s, the coefficients of the product are given by the convolution of the original coefficient sequence
s, extended with zeros where necessary to avoid undefined terms; this is known as the Cauchy product of the coefficients of the two polynomials.

The summation on k is called a periodic summation of the function f.
If gN is a periodic summation of another function, g, then f∗gN is known as a circular convolution
of f and g.
When the non-zero durations of both f and g are limited to the interval [0, N − 1], f∗gN reduces to these common forms:
The notation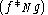 for cyclic convolution denotes convolution over the cyclic group
for cyclic convolution denotes convolution over the cyclic group
of integers modulo N
.
Circular convolution is frequently used to characterized systems analyzed through the lens of the Discrete Fourier Transform.
of multi-digit numbers, which can therefore be efficiently implemented with transform techniques .
requires N arithmetic operations per output value and N2 operations for N outputs. That can be significantly reduced with any of several fast algorithms. Digital signal processing
and other applications typically use fast convolution algorithms to reduce the cost of the convolution to O(N log N) complexity.
The most common fast convolution algorithms use fast Fourier transform
(FFT) algorithms via the circular convolution theorem. Specifically, the circular convolution
of two finite-length sequences is found by taking an FFT of each sequence, multiplying pointwise, and then performing an inverse FFT. Convolutions of the type defined above are then efficiently implemented using that technique in conjunction with zero-extension and/or discarding portions of the output. Other fast convolution algorithms, such as the Schönhage–Strassen algorithm, use fast Fourier transforms in other ring
s.
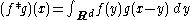
is well-defined only if ƒ and g decay sufficiently rapidly at infinity in order for the integral to exist. Conditions for the existence of the convolution may be tricky, since a blow-up in g at infinity can be easily offset by sufficiently rapid decay in ƒ. The question of existence thus may involve different conditions on ƒ and g.
s, then their convolution exists, and is also compactly supported and continuous . More generally, if either function (say ƒ) is compactly supported and the other is locally integrable
, then the convolution ƒ∗g is well-defined and continuous.
), and in this case ƒ∗g is also integrable . This is a consequence of Tonelli's theorem. Likewise, if ƒ ∈ L1(Rd) and g ∈ Lp(Rd) where 1 ≤ p ≤ ∞, then ƒ∗g ∈ Lp(Rd) and
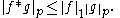
In the particular case p= 1, this shows that L1 is a Banach algebra
under the convolution (and equality of the two sides holds if f and g are non-negative almost everywhere).
More generally, Young's inequality implies that the convolution is a continuous bilinear map between suitable Lp spaces. Specifically, if 1 ≤ p,q,r ≤ ∞ satisfy
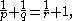
then
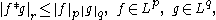
so that the convolution is a continuous bilinear mapping from Lp×Lq to Lr.
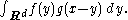
More generally, it is possible to extend the definition of the convolution in a unique way so that the associative law
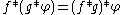
remains valid in the case where ƒ is a distribution, and g a compactly supported distribution .
is the measure λ defined by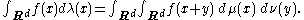
This agrees with the convolution defined above when μ and ν are regarded as distributions, as well as the convolution of L1 functions when μ and ν are absolutely continuous with respect to the Lebesgue measure.
The convolution of measures also satisfies the following version of Young's inequality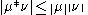
where the norm is the total variation
of a measure. Because the space of measures of bounded variation is a Banach space
, convolution of measures can be treated with standard methods of functional analysis
that may not apply for the convolution of distributions.
without identity
. Other linear spaces of functions, such as the space of continuous functions of compact support, are closed
under the convolution, and so also form commutative algebras.
Commutativity
Associativity
Distributivity
Associativity with scalar multiplication
for any real (or complex) number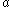 .
.
Multiplicative identity
No algebra of functions possesses an identity for the convolution. The lack of identity is typically not a major inconvenience, since most collections of functions on which the convolution is performed can be convolved with a delta distribution or, at the very least (as is the case of L1) admit approximations to the identity. The linear space of compactly supported distributions does, however, admit an identity under the convolution. Specifically,
where δ is the delta distribution.
Inverse element
Some distributions have an inverse element
for the convolution, S(−1), which is defined by
The set of invertible distributions forms an abelian group
under the convolution.
Complex conjugation
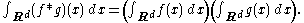
This follows from Fubini's theorem
. The same result holds if ƒ and g are only assumed to be nonnegative measurable functions, by Tonelli's theorem.
where d/dx is the derivative
. More generally, in the case of functions of several variables, an analogous formula holds with the partial derivative
:

A particular consequence of this is that the convolution can be viewed as a "smoothing" operation: the convolution of ƒ and g is differentiable as many times as ƒ and g are together.
These identities hold under the precise condition that ƒ and g are absolutely integrable and at least one of them has an absolutely integrable (L1) weak derivative, as a consequence of Young's inequality
. For instance, when ƒ is continuously differentiable with compact support, and g is an arbitrary locally integrable function,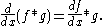
These identities also hold much more broadly in the sense of tempered distributions if one of ƒ or g is a compactly supported distribution or a Schwartz function and the other is a tempered distribution. On the other hand, two positive integrable and infinitely differentiable functions may have a nowhere continuous convolution.
In the discrete case, the difference operator D ƒ(n) = ƒ(n + 1) − ƒ(n) satisfies an analogous relationship:
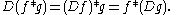
states that
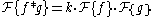
where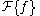 denotes the Fourier transform
denotes the Fourier transform
of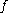 , and
, and 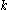 is a constant that depends on the specific normalization
is a constant that depends on the specific normalization
of the Fourier transform (see “Properties of the Fourier transform”). Versions of this theorem also hold for the Laplace transform, two-sided Laplace transform
, Z-transform
and Mellin transform
.
See also the less trivial Titchmarsh convolution theorem
.

where τxƒ is the translation of the function ƒ by x defined by

If ƒ is a Schwartz function, then τxƒ is the convolution with a translated Dirac delta function τxƒ = ƒ∗τx δ. So translation invariance of the convolution of Schwartz functions is a consequence of the associativity of convolution.
Furthermore, under certain conditions, convolution is the most general translation invariant operation. Informally speaking, the following holds
Thus any translation invariant operation can be represented as a convolution. Convolutions play an important role in the study of time-invariant system
s, and especially LTI system theory
. The representing function gS is the impulse response
of the transformation S.
A more precise version of the theorem quoted above requires specifying the class of functions on which the convolution is defined, and also requires assuming in addition that S must be a continuous linear operator
with respect to the appropriate topology
. It is known, for instance, that every continuous translation invariant continuous linear operator on L1 is the convolution with a finite Borel measure. More generally, every continuous translation invariant continuous linear operator on Lp for 1 ≤ p < ∞ is the convolution with a tempered distribution whose Fourier transform
is bounded. To wit, they are all given by bounded Fourier multipliers.
endowed with a measure
λ, and if f and g are real or complex valued integrable functions on G, then we can define their convolution by
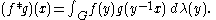
In typical cases of interest G is a locally compact Hausdorff
topological group
and λ is a (left-) Haar measure
. In that case, unless G is unimodular, the convolution defined in this way is not the same as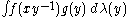 . The preference of one over the other is made so that convolution with a fixed function g commutes with left translation in the group:
. The preference of one over the other is made so that convolution with a fixed function g commutes with left translation in the group:

Furthermore, the convention is also required for consistency with the definition of the convolution of measures given below. However, with a right instead of a left Haar measure, the latter integral is preferred over the former.
On locally compact abelian group
s, a version of the convolution theorem
holds: the Fourier transform of a convolution is the pointwise product of the Fourier transforms. The circle group T with the Lebesgue measure is an immediate example. For a fixed g in L1(T), we have the following familiar operator acting on the Hilbert space
L2(T):

The operator T is compact
. A direct calculation shows that its adjoint T* is convolution with
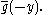
By the commutativity property cited above, T is normal
: T*T = TT*. Also, T commutes with the translation operators. Consider the family S of operators consisting of all such convolutions and the translation operators. Then S is a commuting family of normal operators. According to spectral theory
, there exists an orthonormal basis {hk} that simultaneously diagonalizes S. This characterizes convolutions on the circle. Specifically, we have
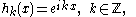
which are precisely the character
s of T. Each convolution is a compact multiplication operator
in this basis. This can be viewed as a version of the convolution theorem discussed above.
A discrete example is a finite cyclic group
of order n. Convolution operators are here represented by circulant matrices, and can be diagonalized by the discrete Fourier transform
.
A similar result holds for compact groups (not necessarily abelian): the matrix coefficients of finite-dimensional unitary representation
s form an orthonormal basis in L2 by the Peter–Weyl theorem
, and an analog of the convolution theorem continues to hold, along with many other aspects of harmonic analysis
that depend on the Fourier transform.
If μ and ν are finite Borel measures on a group G, then their convolution μ∗ν is defined by
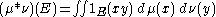
for each measurable subset E of G. The convolution is also a finite measure, whose total variation
satisfies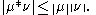
In the case when G is locally compact with (left-)Haar measure
λ, and μ and ν are absolutely continuous
with respect to a λ, so that each has a density function
, then the convolution μ∗ν is also absolutely continuous, and its density function is just the convolution of the two separate density functions.
If μ and ν are probability measure
s, then the convolution μ∗ν is the probability distribution
of the sum X + Y of two independent
random variable
s X and Y whose respective distributions are μ and ν.
with comultiplication Δ, multiplication ∇, unit η, and counit ε. The convolution is a product defined on the endomorphism algebra End(X) as follows. Let φ, ψ ∈ End(X), that is, φ,ψ : X → X are functions that respect all algebraic structure of X, then the convolution φ∗ψ is defined as the composition
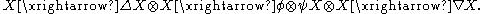
The convolution appears notably in the definition of Hopf algebra
s . A bialgebra is a Hopf algebra if and only if it has an antipode: an endomorphism S such that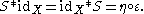
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and, in particular, functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, convolution is a mathematical operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
on two function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation
Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
. It has applications that include probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, image
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, electrical engineering
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, and differential equations.
The convolution can be defined for functions on groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
other than Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. In particular, the circular convolution
Circular convolution
The circular convolution, also known as cyclic convolution, of two aperiodic functions occurs when one of them is convolved in the normal way with a periodic summation of the other function. That situation arises in the context of the Circular convolution theorem...
can be defined for periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s (that is, functions on the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
), and the discrete convolution can be defined for functions on the set of integers. These generalizations of the convolution have applications in the field of numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
and numerical linear algebra
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, and in the design and implementation of finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
filters in signal processing.
Computing the inverse of the convolution operation is known as deconvolution
Deconvolution
In mathematics, deconvolution is an algorithm-based process used to reverse the effects of convolution on recorded data. The concept of deconvolution is widely used in the techniques of signal processing and image processing...
.
History
The operation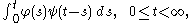
is a particular case of composition products considered by the Italian mathematician Vito Volterra
Vito Volterra
Vito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
in 1913.
Convolution is also sometimes called "Faltung" (which means folding in German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
); both Faltung and convolution were used as early as 1903, though the definition is rather unfamiliar in older uses.
The term Faltung was sometimes used in English through the 1940s, before the notion of convolution became widely used, along with other terms such as composition product, superposition integral, and Carson's integral.
Definition
The convolution of ƒ and g is written ƒ∗g, using an asteriskAsterisk
An asterisk is a typographical symbol or glyph. It is so called because it resembles a conventional image of a star. Computer scientists and mathematicians often pronounce it as star...
or star. It is defined as the integral of the product of the two functions after one is reversed and shifted. As such, it is a particular kind of integral transform:
 |
 |
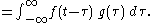 (commutativity) (commutativity) |
While the symbol t is used above, it need not represent the time domain. But in that context, the convolution formula can be described as a weighted average of the function ƒ(τ) at the moment t where the weighting is given by g(−τ) simply shifted by amount t. As t changes, the weighting function emphasizes different parts of the input function.
More generally, if f and g are complex-valued functions on Rd, then their convolution may be defined as the integral:

| Visual explanation of convolution. |
|
|---|---|
|
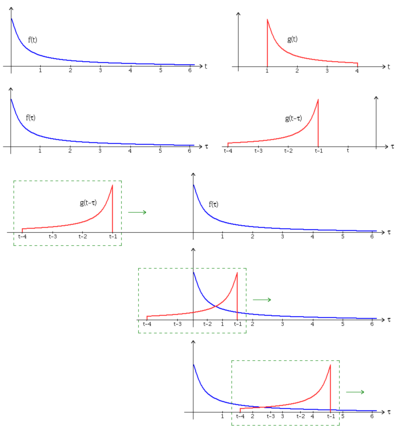 |
Circular convolution
When a function gT is periodic, with period T, then for functions, ƒ, such that ƒ∗gT exists, the convolution is also periodic and identical to: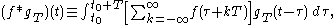
where to is an arbitrary choice. The summation is called a periodic summation of the function ƒ.
If gT is a periodic summation of another function, g, then ƒ∗gT is known as a circular, cyclic, or periodic convolution of ƒ and g.
Discrete convolution
For complex-valued functions f, g defined on the set Z of integers, the discrete convolution of f and g is given by: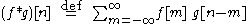
-
-
-
 (commutativity)
(commutativity)
-
-
When multiplying two polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, the coefficients of the product are given by the convolution of the original coefficient sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s, extended with zeros where necessary to avoid undefined terms; this is known as the Cauchy product of the coefficients of the two polynomials.
Circular discrete convolution
When a function gN is periodic, with period N, then for functions, f, such that f∗gN exists, the convolution is also periodic and identical to:
The summation on k is called a periodic summation of the function f.
If gN is a periodic summation of another function, g, then f∗gN is known as a circular convolution
Circular convolution
The circular convolution, also known as cyclic convolution, of two aperiodic functions occurs when one of them is convolved in the normal way with a periodic summation of the other function. That situation arises in the context of the Circular convolution theorem...
of f and g.
When the non-zero durations of both f and g are limited to the interval [0, N − 1], f∗gN reduces to these common forms:
The notation
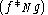 for cyclic convolution denotes convolution over the cyclic group
for cyclic convolution denotes convolution over the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of integers modulo N
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
.
Circular convolution is frequently used to characterized systems analyzed through the lens of the Discrete Fourier Transform.
Fast convolution algorithms
In many situations, discrete convolutions can be converted to circular convolutions so that fast transforms with a convolution property can be used to implement the computation. For example, convolution of digit sequences is the kernel operation in multiplicationMultiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of multi-digit numbers, which can therefore be efficiently implemented with transform techniques .
requires N arithmetic operations per output value and N2 operations for N outputs. That can be significantly reduced with any of several fast algorithms. Digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
and other applications typically use fast convolution algorithms to reduce the cost of the convolution to O(N log N) complexity.
The most common fast convolution algorithms use fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithms via the circular convolution theorem. Specifically, the circular convolution
Circular convolution
The circular convolution, also known as cyclic convolution, of two aperiodic functions occurs when one of them is convolved in the normal way with a periodic summation of the other function. That situation arises in the context of the Circular convolution theorem...
of two finite-length sequences is found by taking an FFT of each sequence, multiplying pointwise, and then performing an inverse FFT. Convolutions of the type defined above are then efficiently implemented using that technique in conjunction with zero-extension and/or discarding portions of the output. Other fast convolution algorithms, such as the Schönhage–Strassen algorithm, use fast Fourier transforms in other ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s.
Domain of definition
The convolution of two complex-valued functions on Rd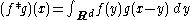
is well-defined only if ƒ and g decay sufficiently rapidly at infinity in order for the integral to exist. Conditions for the existence of the convolution may be tricky, since a blow-up in g at infinity can be easily offset by sufficiently rapid decay in ƒ. The question of existence thus may involve different conditions on ƒ and g.
Compactly supported functions
If ƒ and g are compactly supported continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s, then their convolution exists, and is also compactly supported and continuous . More generally, if either function (say ƒ) is compactly supported and the other is locally integrable
Locally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
, then the convolution ƒ∗g is well-defined and continuous.
Integrable functions
The convolution of ƒ and g exists if ƒ and g are both Lebesgue integrable functions (in L1(Rd)Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
), and in this case ƒ∗g is also integrable . This is a consequence of Tonelli's theorem. Likewise, if ƒ ∈ L1(Rd) and g ∈ Lp(Rd) where 1 ≤ p ≤ ∞, then ƒ∗g ∈ Lp(Rd) and
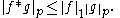
In the particular case p= 1, this shows that L1 is a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
under the convolution (and equality of the two sides holds if f and g are non-negative almost everywhere).
More generally, Young's inequality implies that the convolution is a continuous bilinear map between suitable Lp spaces. Specifically, if 1 ≤ p,q,r ≤ ∞ satisfy
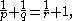
then
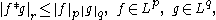
so that the convolution is a continuous bilinear mapping from Lp×Lq to Lr.
Functions of rapid decay
In addition to compactly supported functions and integrable functions, functions that have sufficiently rapid decay at infinity can also be convolved. An important feature of the convolution is that if ƒ and g both decay rapidly, then ƒ∗g also decays rapidly. In particular, if ƒ and g are rapidly decreasing functions, then so is the convolution ƒ∗g. Combined with the fact that convolution commutes with differentiation (see Properties), it follows that the class of Schwartz functions is closed under convolution.Distributions
Under some circumstances, it is possible to define the convolution of a function with a distribution, or of two distributions. If ƒ is a compactly supported function and g is a distribution, then ƒ∗g is a smooth function defined by a distributional formula analogous to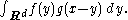
More generally, it is possible to extend the definition of the convolution in a unique way so that the associative law
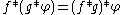
remains valid in the case where ƒ is a distribution, and g a compactly supported distribution .
Measures
The convolution of any two Borel measures μ and ν of bounded variationBounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
is the measure λ defined by
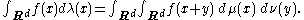
This agrees with the convolution defined above when μ and ν are regarded as distributions, as well as the convolution of L1 functions when μ and ν are absolutely continuous with respect to the Lebesgue measure.
The convolution of measures also satisfies the following version of Young's inequality
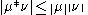
where the norm is the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
of a measure. Because the space of measures of bounded variation is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, convolution of measures can be treated with standard methods of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
that may not apply for the convolution of distributions.
Algebraic properties
The convolution defines a product on the linear space of integrable functions. This product satisfies the following algebraic properties, which formally mean that the space of integrable functions with the product given by convolution is a commutative algebraCommutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
without identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. Other linear spaces of functions, such as the space of continuous functions of compact support, are closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the convolution, and so also form commutative algebras.
Commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
Associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
Distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
Associativity with scalar multiplication
for any real (or complex) number
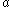 .
.Multiplicative identity
No algebra of functions possesses an identity for the convolution. The lack of identity is typically not a major inconvenience, since most collections of functions on which the convolution is performed can be convolved with a delta distribution or, at the very least (as is the case of L1) admit approximations to the identity. The linear space of compactly supported distributions does, however, admit an identity under the convolution. Specifically,

where δ is the delta distribution.
Inverse element
Some distributions have an inverse element
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
for the convolution, S(−1), which is defined by
The set of invertible distributions forms an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under the convolution.
Complex conjugation
Integration
If ƒ and g are integrable functions, then the integral of their convolution on the whole space is simply obtained as the product of their integrals: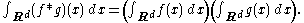
This follows from Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
. The same result holds if ƒ and g are only assumed to be nonnegative measurable functions, by Tonelli's theorem.
Differentiation
In the one-variable case,where d/dx is the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. More generally, in the case of functions of several variables, an analogous formula holds with the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
:

A particular consequence of this is that the convolution can be viewed as a "smoothing" operation: the convolution of ƒ and g is differentiable as many times as ƒ and g are together.
These identities hold under the precise condition that ƒ and g are absolutely integrable and at least one of them has an absolutely integrable (L1) weak derivative, as a consequence of Young's inequality
Young's inequality
In mathematics, the term Young's inequality is used for two inequalities: one about the product of two numbers, and one about the convolution of two functions. They are named for William Henry Young....
. For instance, when ƒ is continuously differentiable with compact support, and g is an arbitrary locally integrable function,
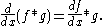
These identities also hold much more broadly in the sense of tempered distributions if one of ƒ or g is a compactly supported distribution or a Schwartz function and the other is a tempered distribution. On the other hand, two positive integrable and infinitely differentiable functions may have a nowhere continuous convolution.
In the discrete case, the difference operator D ƒ(n) = ƒ(n + 1) − ƒ(n) satisfies an analogous relationship:
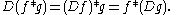
Convolution theorem
The convolution theoremConvolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
states that
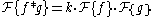
where
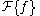 denotes the Fourier transform
denotes the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of
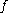 , and
, and 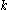 is a constant that depends on the specific normalization
is a constant that depends on the specific normalizationNormalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
of the Fourier transform (see “Properties of the Fourier transform”). Versions of this theorem also hold for the Laplace transform, two-sided Laplace transform
Two-sided Laplace transform
In mathematics, the two-sided Laplace transform or bilateral Laplace transform is an integral transform closely related to the Fourier transform, the Mellin transform, and the ordinary or one-sided Laplace transform...
, Z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
and Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
.
See also the less trivial Titchmarsh convolution theorem
Titchmarsh convolution theorem
The Titchmarsh convolution theorem is named after Edward Charles Titchmarsh,a British mathematician. The theorem describes the properties of the support of the convolution of two functions.- Titchmarsh convolution theorem :...
.
Translation invariance
The convolution commutes with translations, meaning that
where τxƒ is the translation of the function ƒ by x defined by

If ƒ is a Schwartz function, then τxƒ is the convolution with a translated Dirac delta function τxƒ = ƒ∗τx δ. So translation invariance of the convolution of Schwartz functions is a consequence of the associativity of convolution.
Furthermore, under certain conditions, convolution is the most general translation invariant operation. Informally speaking, the following holds
- Suppose that S is a linear operator acting on functions which commutes with translations: S(τxƒ) = τx(Sƒ) for all x. Then S is given as convolution with a function (or distribution) gS; that is Sƒ = gS∗ƒ.
Thus any translation invariant operation can be represented as a convolution. Convolutions play an important role in the study of time-invariant system
Time-invariant system
A time-invariant system is one whose output does not depend explicitly on time.This property can be satisfied if the transfer function of the system is not a function of time except expressed by the input and output....
s, and especially LTI system theory
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
. The representing function gS is the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of the transformation S.
A more precise version of the theorem quoted above requires specifying the class of functions on which the convolution is defined, and also requires assuming in addition that S must be a continuous linear operator
Continuous linear operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
with respect to the appropriate topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. It is known, for instance, that every continuous translation invariant continuous linear operator on L1 is the convolution with a finite Borel measure. More generally, every continuous translation invariant continuous linear operator on Lp for 1 ≤ p < ∞ is the convolution with a tempered distribution whose Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is bounded. To wit, they are all given by bounded Fourier multipliers.
Convolutions on groups
If G is a suitable groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
endowed with a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
λ, and if f and g are real or complex valued integrable functions on G, then we can define their convolution by
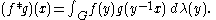
In typical cases of interest G is a locally compact Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and λ is a (left-) Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
. In that case, unless G is unimodular, the convolution defined in this way is not the same as
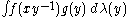 . The preference of one over the other is made so that convolution with a fixed function g commutes with left translation in the group:
. The preference of one over the other is made so that convolution with a fixed function g commutes with left translation in the group:
Furthermore, the convention is also required for consistency with the definition of the convolution of measures given below. However, with a right instead of a left Haar measure, the latter integral is preferred over the former.
On locally compact abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, a version of the convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
holds: the Fourier transform of a convolution is the pointwise product of the Fourier transforms. The circle group T with the Lebesgue measure is an immediate example. For a fixed g in L1(T), we have the following familiar operator acting on the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
L2(T):

The operator T is compact
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
. A direct calculation shows that its adjoint T* is convolution with
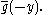
By the commutativity property cited above, T is normal
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
: T*T = TT*. Also, T commutes with the translation operators. Consider the family S of operators consisting of all such convolutions and the translation operators. Then S is a commuting family of normal operators. According to spectral theory
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
, there exists an orthonormal basis {hk} that simultaneously diagonalizes S. This characterizes convolutions on the circle. Specifically, we have
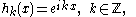
which are precisely the character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
s of T. Each convolution is a compact multiplication operator
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
in this basis. This can be viewed as a version of the convolution theorem discussed above.
A discrete example is a finite cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order n. Convolution operators are here represented by circulant matrices, and can be diagonalized by the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
.
A similar result holds for compact groups (not necessarily abelian): the matrix coefficients of finite-dimensional unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s form an orthonormal basis in L2 by the Peter–Weyl theorem
Peter–Weyl theorem
In mathematics, the Peter–Weyl theorem is a basic result in the theory of harmonic analysis, applying to topological groups that are compact, but are not necessarily abelian. It was initially proved by Hermann Weyl, with his student Fritz Peter, in the setting of a compact topological group G...
, and an analog of the convolution theorem continues to hold, along with many other aspects of harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
that depend on the Fourier transform.
Convolution of measures
Let G be a topological group.If μ and ν are finite Borel measures on a group G, then their convolution μ∗ν is defined by
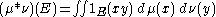
for each measurable subset E of G. The convolution is also a finite measure, whose total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
satisfies
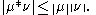
In the case when G is locally compact with (left-)Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
λ, and μ and ν are absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
with respect to a λ, so that each has a density function
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
, then the convolution μ∗ν is also absolutely continuous, and its density function is just the convolution of the two separate density functions.
If μ and ν are probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s, then the convolution μ∗ν is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the sum X + Y of two independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y whose respective distributions are μ and ν.
Bialgebras
Let (X, Δ, ∇, ε, η) be a bialgebraBialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
with comultiplication Δ, multiplication ∇, unit η, and counit ε. The convolution is a product defined on the endomorphism algebra End(X) as follows. Let φ, ψ ∈ End(X), that is, φ,ψ : X → X are functions that respect all algebraic structure of X, then the convolution φ∗ψ is defined as the composition
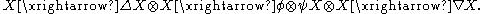
The convolution appears notably in the definition of Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s . A bialgebra is a Hopf algebra if and only if it has an antipode: an endomorphism S such that
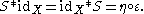
Applications
Convolution and related operations are found in many applications of engineering and mathematics.- In electrical engineeringElectrical engineeringElectrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, the convolution of one function (the input signal) with a second function (the impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
) gives the output of a linear time-invariant system (LTI). At any given moment, the output is an accumulated effect of all the prior values of the input function, with the most recent values typically having the most influence (expressed as a multiplicative factor). The impulse response function provides that factor as a function of the elapsed time since each input value occurred.- In digital signal processingDigital signal processingDigital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
and image processingImage processingIn electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
applications, the entire input function is often available for computing every sample of the output function. In that case, the constraint that each output is the effect of only prior inputs can be relaxed. - Convolution amplifies or attenuates each frequency component of the input independently of the other components.
- In digital signal processing
- In statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, as noted above, a weighted moving averageMoving average modelIn time series analysis, the moving-average model is a common approach for modeling univariate time series models. The notation MA refers to the moving average model of order q:...
is a convolution. - In probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the sum of two independent random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s is the convolution of their individual distributions. - In opticsOpticsOptics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, many kinds of "blur" are described by convolutions. A shadowShadowA shadow is an area where direct light from a light source cannot reach due to obstruction by an object. It occupies all of the space behind an opaque object with light in front of it. The cross section of a shadow is a two-dimensional silhouette, or reverse projection of the object blocking the...
(e.g., the shadow on the table when you hold your hand between the table and a light source) is the convolution of the shapeShapeThe shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
of the light source that is casting the shadow and the object whose shadow is being cast. An out-of-focus photograph is the convolution of the sharp image with the shape of the iris diaphragm. The photographic term for this is bokehBokehIn photography, bokeh is the blur, or the aesthetic quality of the blur, in out-of-focus areas of an image, or "the way the lens renders out-of-focus points of light."...
. - Similarly, in digital image processingDigital image processingDigital image processing is the use of computer algorithms to perform image processing on digital images. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing...
, convolutional filtering plays an important role in many important algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s in edge detectionEdge detectionEdge detection is a fundamental tool in image processing and computer vision, particularly in the areas of feature detection and feature extraction, which aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities...
and related processes. - In linear acousticsAcousticsAcoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
, an echo is the convolution of the original sound with a function representing the various objects that are reflecting it. - In artificial reverberationReverberationReverberation is the persistence of sound in a particular space after the original sound is removed. A reverberation, or reverb, is created when a sound is produced in an enclosed space causing a large number of echoes to build up and then slowly decay as the sound is absorbed by the walls and air...
(digital signal processingDigital signal processingDigital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
, pro audio), convolution is used to map the impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of a real room on a digital audio signal (see previous and next point for additional information). - In time-resolved fluorescence spectroscopyFluorescence spectroscopyFluorescence spectroscopy aka fluorometry or spectrofluorometry, is a type of electromagnetic spectroscopy which analyzes fluorescence from a sample. It involves using a beam of light, usually ultraviolet light, that excites the electrons in molecules of certain compounds and causes them to emit...
, the excitation signal can be treated as a chain of delta pulses, and the measured fluorescence is a sum of exponential decays from each delta pulse. - In radiotherapy treatment planning systems, most part of all modern codes of calculation applies a convolution-superposition algorithm.
- In physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, wherever there is a linear systemLinear systemA linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
with a "superposition principleSuperposition principleIn physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
", a convolution operation makes an appearance. - In kernel density estimationKernel density estimationIn statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...
, a distribution is estimated from sample points by convolution with a kernel, such as an isotropic Gaussian. . - In computational fluid dynamicsComputational fluid dynamicsComputational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
, the large eddy simulationLarge eddy simulationLarge eddy simulation is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and many of the issues unique to LES were first explored by Deardorff...
(LES) turbulence model uses the convolution operation to lower the range of length scales necessary in computation thereby reducing computational cost.
See also
- LTI system theory#Impulse response and convolution
- Toeplitz matrixToeplitz matrixIn linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
(convolutions can be considered a Toeplitz matrix operation where each row is a shifted copy of the convolution kernel)- Circulant matrixCirculant matrixIn linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
- Circulant matrix
- Cross-correlationCross-correlationIn signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
- DeconvolutionDeconvolutionIn mathematics, deconvolution is an algorithm-based process used to reverse the effects of convolution on recorded data. The concept of deconvolution is widely used in the techniques of signal processing and image processing...
- Dirichlet convolutionDirichlet convolutionIn mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
- Titchmarsh convolution theoremTitchmarsh convolution theoremThe Titchmarsh convolution theorem is named after Edward Charles Titchmarsh,a British mathematician. The theorem describes the properties of the support of the convolution of two functions.- Titchmarsh convolution theorem :...
- Convolution powerConvolution powerIn mathematics, the convolution power is the n-fold iteration of the convolution with itself. Thus if x is a function on Euclidean space Rd and n is a natural number, then the convolution power is defined by...
- Analog signal processingAnalog signal processingAnalog signal processing is any signal processing conducted on analog signals by analog means. "Analog" indicates something that is mathematically represented as a set of continuous values. This differs from "digital" which uses a series of discrete quantities to represent signal...
- Convolution for optical broad-beam responses in scattering mediaConvolution for optical broad-beam responses in scattering mediaPhoton transport theories, such as the Monte Carlo method, are commonly used to model light propagation in tissue. The responses to a pencil beam incident on a scattering medium are referred to as Green’s functions or impulse responses. Photon transport methods can be directly used to compute...
- List of convolutions of probability distributions
- Jan MikusinskiJan MikusinskiProf. Jan Mikusiński was a Polish mathematician known for his pioneering work in mathematical analysis. Mikusiński developed an operational calculus - 44A40 Calculus of Mikusiński, which is relevant for solving differential equations...
External links
- Earliest Uses: The entry on Convolution has some historical information.
- Convolution, on The Data Analysis BriefBook
- http://www.jhu.edu/~signals/convolve/index.html Visual convolution Java Applet.
- http://www.jhu.edu/~signals/discreteconv2/index.html Visual convolution Java Applet for discrete-time functions.
- Lectures on Image Processing: A collection of 18 lectures in pdf format from Vanderbilt University. Lecture 7 is on 2-D convolution., by Alan Peters.
- http://www.vuse.vanderbilt.edu/~rap2/EECE253/EECE253_01_Intro.pdf
- Convolution Kernel Mask Operation Interactive tutorial
- Convolution at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Freeverb3 Impulse Response Processor: Opensource zero latency impulse response processor with VST plugins
- Stanford University CS 178 interactive Flash demo showing how spatial convolution works.


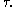
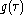 →
→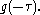
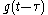 to slide along the
to slide along the  -axis.
-axis. , where the weighting function is
, where the weighting function is