In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, kernel density estimation is a non-parametric

Non-parametric statistics

In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...

 way of estimating

Density estimation

In probability and statistics,density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function...

 the probability density function

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

 of a random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

. Kernel density estimation is a fundamental data smoothing problem where inferences about the population

Statistical population

A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...

 are made, based on a finite data sample. In some fields such as signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

 and econometrics

Econometrics

Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...

 it is also known as the Parzen–Rosenblatt window method, after Emanuel Parzen

Emanuel Parzen

Emanuel Parzen is an American statistician. He has worked and published on signal detection theory and time series analysis, where he pioneered the use of kernel density estimation . Parzen is the recipient of the 1994 Samuel S...

 and Murray Rosenblatt

Murray Rosenblatt

Murray Rosenblatt is a statistician specializing in time series analysis who is a Professor ofmathematics at University of California, San Diego. He received his Ph.D. at Cornell University....

, who are usually credited with independently creating it in its current form.

Definition

Let (x₁, x₂, …, x_n) be an iid sample drawn from some distribution with an unknown density

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

 ƒ. We are interested in estimating the shape of this function ƒ. Its kernel density estimator is

where K(•) is the kernel

Kernel (statistics)

A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...

 — a symmetric but not necessarily positive function that integrates to one — and is a smoothing

Smoothing

In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...

 parameter called the bandwidth. A kernel with subscript h is called the scaled kernel and defined as . Intuitively one wants to choose h as small as the data allows, however there is always a trade-off between the bias of the estimator and its variance; more on the choice of bandwidth later. A range of kernel function

Kernel (statistics)

A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...

s are commonly used: uniform, triangular, biweight, triweight, Epanechnikov, normal, and others. The Epanechnikov kernel is optimal in a minimum variance sense, though the loss of efficiency is small for the kernels listed previously, and due to its convenient mathematical properties, the normal kernel
is often used , where ϕ is the standard normal density function.

Kernel density estimates are closely related to histograms, although the former have several advantages. We compare the construction of histogram and kernel density estimators, using these 6 data points: x₁=-2.1, x₂=-1.3, x₃=-0.4, x₄=1.9, x₅=5.1, x₆=6.2. For the histogram, first the horizontal axis is divided into sub-intervals or bins which cover the range of the data. In this case, we have 6 bins each of width 2. Whenever a data point falls inside this interval, we place a box of height 1/12. If more than one data point falls inside the same bin, we stack the boxes on top of each other. For the kernel density estimate, we place a normal kernel with variance 2.25 (indicated by the red dashed lines) on each of the data points x_i. The kernels are summed to make the kernel density estimate (solid blue curve). The smoothness of the kernel density estimate is evident compared to the discreteness of the histogram. This discrete appearance is a result from the inherent statistical inefficiency of histograms as compared to kernel estimators.
The construction of a kernel density estimate finds interpretations in fields outside of density estimation. For example, in thermodynamics

Thermodynamics

Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...

, this is equivalent to amount of heat generated when heat kernel

Heat kernel

In the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a particular domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some...

s (the fundamental solution to the heat equation

Heat equation

The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...

) are placed at the locations x_i. Similar methods are used to construct Discrete Laplace operator

Discrete Laplace operator

In mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...

s on point clouds for manifold learning.

Relation to the characteristic function density estimator

Given the sample (x₁, x₂, …, x_n), it is natural to estimate the characteristic function

Characteristic function (probability theory)

In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...

  as

Knowing the characteristic function it is possible to find the corresponding probability density function through the inverse Fourier transform formula. One difficulty with applying this inversion formula is that it leads to a diverging integral since the estimate $\backslash scriptstyle\backslash hat\backslash varphi(t)$ is unreliable for large t’s. In order to circumvent this problem the estimator $\backslash scriptstyle\backslash hat\backslash varphi(t)$ is multiplied by a damping function , which is equal to 1 at the origin, and then falls to 0 at infinity. The “bandwidth parameter” h controls how fast we try to dampen the function $\backslash scriptstyle\backslash hat\backslash varphi(t)$. In particular when h is small, then ψ_h(t) will be approximately one for a large range of t’s, which means that $\backslash scriptstyle\backslash hat\backslash varphi(t)$ remains practically unaltered in the most important region of t’s.

The most common choice for function ψ is either the uniform function }, which effectively means truncating the interval of integration in the inversion formula to , or the gaussian function . Once the function ψ has been chosen, the inversion formula may be applied, and the density estimator will be

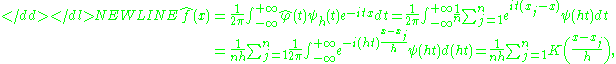
where K is the inverse Fourier transform of the damping function ψ. Thus the kernel density estimator coincides with the characteristic function density estimator.

Bandwidth selection

The bandwidth of the kernel is a free parameter

Free parameter

A free parameter is a variable used in a mathematical model and for scientific modelling which allows adjustments so the models can provide helpful insights. The values of free parameters used in models are provided by previous experiments and by educated guesses....

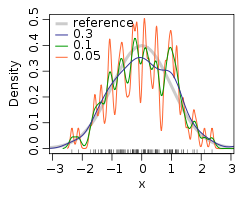
 which exhibits a strong influence on the resulting estimate. To illustrate its effect, we take a simulated random sample from the standard normal distribution (plotted at the blue spikes in the rug plot on the horizontal axis). The grey curve is the true density (a normal density with mean 0 and variance 1). In comparison, the red curve is undersmoothed since it contains too much spurious data artifacts arising from using a bandwidth h=0.05 which is too small. The green curve is oversmoothed since using the bandwidth h=2 obscures much of the underlying structure. The black curve is considered to be optimally smoothed since its density estimate is close to the true density.

The most common optimality criterion used to the select this parameter is the expected L₂ risk function

Risk function

In decision theory and estimation theory, the risk function R of a decision rule, δ, is the expected value of a loss function L:...

, also known as the mean integrated squared error

Under weak assumptions on ƒ and K,
MISE (h) = AMISE(h) + o(1/(nh) + h⁴) where o is the little o notation.
The AMISE is the Asymptotic MISE which consists of the two leading terms


where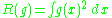 for a function g,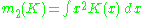
and ƒ' is the second derivative of ƒ. The minimum of this AMISE is the solution to this differential equation


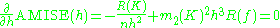
or


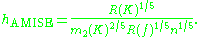
Neither the AMISE nor the h_AMISE formulas are able to be used directly since they involve the unknown density function ƒ or its second derivative ƒ', so a variety of automatic, data-based methods have been developed for selecting the bandwidth. Many review studies have been carried out to compare their efficacities, with the general consensus that the plug-in selectors and cross validation selectors are the most useful over a wide range of data sets.

Substituting any bandwidth h which has the same asymptotic order n^-1/5 as h_AMISE into the AMISE
gives that AMISE(h) = O(n^-4/5), where O is the big o notation

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

. It can be shown that, under weak assumptions, there cannot exist a non-parametric estimator that converges at a faster rate than the kernel estimator. Note that the n^−4/5 rate is slower than the typical n⁻¹ convergence rate of parametric methods.

If the bandwidth is not held fixed, but is varied depending upon the location
of either the estimate (balloon estimator)
or the samples (pointwise estimator), this produces a particularly powerful method
known as adaptive or variable bandwidth kernel density estimation

Variable kernel density estimation

In statistics, adaptive or "variable-bandwidth" kernel density estimation is a form of kernel density estimation in which the size of the kernels used in the estimate are varied...

.

Practical estimation of the bandwidth

If Gaussian basis functions are used to approximate univariate data, and the underlying density being estimated is Gaussian then it can be shown that the optimal choice for h is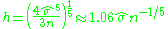, where 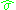is the standard deviation of the samples.
This approximation is known as the normal distribution approximation, Gaussian approximation, or Silverman's rule of thumb.

Statistical implementation

A non-exhaustive list of software implementations of kernel density estimators includes:

• In C
  C (programming language)
  C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
  
  /C++
  C++
  C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
  
  , FIGTree is a library that can be used to compute kernel density estimates using normal kernels. MATLAB interface available.
• In CrimeStat
  CrimeStat
  CrimeStat is a Windows-based spatial statistic software program that conducts spatial and statistical analysis and is designed to interface with a Geographic Information System. The program is developed by Ned Levine & Associates, with funding by the National Institute of Justice...
  
  , kernel density estimation is implemented using five different kernel functions - normal, uniform, quartic, negative exponential, and triangular. Both single- and dual-kernel density estimate routines are available. Kernel density estimation is also used in interpolating a Head Bang routine, in estimating a two-dimensional Journey-to-crime density function, and in estimating a three-dimensional Bayesian Journey-to-crime estimate.
• In ESRI
  ESRI
  Esri is a software development and services company providing Geographic Information System software and geodatabase management applications. The headquarters of Esri is in Redlands, California....
  
   products, kernel density mapping is managed out of the Spatial Analyst toolbox and uses the Epanechnikov kernel.
• In gnuplot
  Gnuplot
  - License :Despite gnuplot's name, it is not part of or related to the GNU system and it is not distributed under the GNU General Public License .However, some GNU packages do use gnuplot....
  
  , kernel density estimation is implemented by the smooth kdensity option, the datafile can contain a weight and bandwidth for each point, or the bandwidth can be set automatically.
• In Haskell
  Haskell (programming language)
  Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
  
  , kernel density is implemented in the statistics package.
• In Java
  Java (programming language)
  Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
  
  , the Weka (machine learning)
  Weka (machine learning)
  Weka is a popular suite of machine learning software written in Java, developed at the University of Waikato, New Zealand...
  
   package provides weka.estimators.KernelEstimator, among others.
• In Javascript, the visualization package D3 offers a KDE package in its science.stats package.
• In JMP
  JMP
  JMP may refer to:* JMP , a statistical analysis application by SAS Institute, Inc.* JMP * Jean-Marie Pfaff, a Belgian football goalkeeper* Joint Monitoring Programme for Water Supply and Sanitation...
  
  , The Fit Y by X platform can be used to estimate univariate and bivariate kernel densitities.
• In MATLAB
  MATLAB
  MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
  
  , kernel density estimation is implemented through the ksdensity function (Statistics Toolbox). This function does not provide an automatic data-driven bandwidth but uses a rule of thumb
  Rule of thumb
  A rule of thumb is a principle with broad application that is not intended to be strictly accurate or reliable for every situation. It is an easily learned and easily applied procedure for approximately calculating or recalling some value, or for making some determination...
  
  , which is optimal only when the target density is normal. A free MATLAB software package which implements an automatic bandwidth selection method is available from the MATLAB Central File Exchange for 1 dimensional data and for 2 dimensional data.
• In Mathematica
  Mathematica
  Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
  
  , numeric kernel density estimation is implemented by the function SmoothKernelDistribution here and symbolic estimation is implemented using the function KernelMixtureDistribution here both of which provide data-driven bandwidths.
• In Octave
  GNU Octave
  GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...
  
  , kernel density estimation is implemented by the kernel_density option (econometrics package).
• In Perl
  Perl
  Perl is a high-level, general-purpose, interpreted, dynamic programming language. Perl was originally developed by Larry Wall in 1987 as a general-purpose Unix scripting language to make report processing easier. Since then, it has undergone many changes and revisions and become widely popular...
  
  , an implementation can be found in the Statistics-KernelEstimation module
• In R
  R (programming language)
  R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
  
  , it is implemented through the density and the bkde function in the KernSmooth library (both included in the base distribution), the kde function in the ks library, the npudens function in the np library (numeric and categorical data), the sm.density function in the sm library. For an implementation of the kde.R function, which does not require installing any packages or libraries, see kde.R.
• In SAS
  SAS System
  SAS is an integrated system of software products provided by SAS Institute Inc. that enables programmers to perform:* retrieval, management, and mining* report writing and graphics* statistical analysis...
  
  , proc kde can be used to estimate univariate and bivariate kernel densities.
• In SciPy
  SciPy
  SciPy is an open source library of algorithms and mathematical tools for the Python programming language.SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and...
  
  , scipy.stats.gaussian_kde can be used to perform gaussian kernel density estimation in arbitrary dimensions, including bandwidth estimation.
• In Stata
  Stata
  Stata is a general-purpose statistical software package created in 1985 by StataCorp. It is used by many businesses and academic institutions around the world...
  
  , it is implemented through kdensity; for example histogram x, kdensity. Alternatively a free Stata module KDENS is available from here allowing a user to estimate 1D or 2D density functions.
• In Analytica release 4.4, the Smoothing option for PDF results uses KDE, and from expressions it is available via the built-in Pdf function.
• In C++
  C++
  C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
  
  , libagf is a library for variable kernel density estimation
  Variable kernel density estimation
  In statistics, adaptive or "variable-bandwidth" kernel density estimation is a form of kernel density estimation in which the size of the kernels used in the estimate are varied...
  
  .

Example in Matlab/octave

For this example, the data are a synthetic sample of 50 points drawn from the standard normal and 50 points from a normal distribution with mean 3.5 and variance 1. The automatic bandwidth selection and density estimation with normal kernels is carried out by kde.m. This function implements a novel automatic bandwidth selector that does not rely on the commonly used Gaussian plug-in rule of thumb

Rule of thumb

A rule of thumb is a principle with broad application that is not intended to be strictly accurate or reliable for every situation. It is an easily learned and easily applied procedure for approximately calculating or recalling some value, or for making some determination...

 heuristic.

 randn('seed',8192);

 x = [randn(50,1); randn(50,1)+3.5];

 [h, fhat, xgrid] = kde(x, 401);

 figure;

 hold on;

 plot(xgrid, fhat, 'linewidth', 2, 'color', 'black');

 plot(x, zeros(100,1), 'b+');

 xlabel('x')

 ylabel('Density function')

 hold off;

Example in R

This example is based on the Old Faithful Geyser

Old Faithful Geyser

Old Faithful is a cone geyser located in Wyoming, in Yellowstone National Park in the United States. Old Faithful was named in 1870 during the Washburn-Langford-Doane Expedition and was the first geyser in the park to receive a name...

, a tourist attraction
located in Yellowstone National Park. This famous dataset containing
272 records consists of two variables, eruption duration (minutes) and
waiting time until the next eruption (minutes), included in the base distribution of R.
We analyse the waiting times, using the ks library since it has a wide range of visualisation options.
The bandwidth function is hpi which in turn calls the dpik function
in the KernSmooth library: these functions implement the plug-in selector.
The kernel density estimate using the normal kernel is computed using kde which calls bkde from
KernSmooth. The plot function allows the addition of the data points as a rug plot on the horizontal axis. The bimodal structure in the density estimate of the waiting times is clearly seen, in contrast to the rug plot where this structure is not apparent.

 library(ks)

 attach(faithful)

 h <- hpi(x=waiting)

 fhat <- kde(x=waiting, h=h)

 plot(fhat, drawpoints=TRUE)

See also

• Kernel (statistics)
  Kernel (statistics)
  A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...
  
  
• Kernel (mathematics)
  Kernel (mathematics)
  In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
  
  
• Kernel smoothing
• Kernel regression
  Kernel regression
  The kernel regression is a non-parametric technique in statistics to estimate the conditional expectation of a random variable. The objective is to find a non-linear relation between a pair of random variables X and Y....
  
  
• Mean-shift
  Mean-shift
  Mean shift is a non-parametric feature-space analysis technique, a so-called mode seeking algorithm. Application domains include clustering in computer vision and image processing.- Overview :...
  
  
• Scale space
  Scale space
  Scale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision...
  
   The triplets {(x, h, KDE with bandwidth h evaluated at x: all x, h>0} form a scale space
  Scale space
  Scale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision...
  
   representation of the data.
• Multivariate kernel density estimation
  Multivariate kernel density estimation
  Kernel density estimation is a nonparametric technique for density estimation i.e., estimation of probability density functions, which is one of the fundamental questions in statistics. It can be viewed as a generalisation of histogram density estimation with improved statistical properties...
  
  

External links

• Introduction to kernel density estimation A short tutorial which motivates kernel density estimators as an improvement over histograms.
• Kernel Bandwidth Optimization A free online tool that instantly generates an optimized kernel density estimate of your data.
• Free Online Software (Calculator) computes the Kernel Density Estimation for any data series according to the following Kernels: Gaussian, Epanechnikov, Rectangular, Triangular, Biweight, Cosine, and Optcosine.
• Kernel Density Estimation Applet An online interactive example of kernel density estimation. Requires .NET 3.0 or later.

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.