Discrete Laplace operator
Encyclopedia
In mathematics
, the discrete Laplace operator is an analog of the continuous Laplace operator
, defined so that it has meaning on a graph
or a discrete grid
. For the case of a finite-dimensional graph (having a finite number of edges and vertices), the discrete Laplace operator is more commonly called the Laplacian matrix
.
The discrete Laplace operator occurs in physics
problems such as the Ising model
and loop quantum gravity
, as well as in the study of discrete dynamical system
s. It is also used in numerical analysis
as a stand-in for the continuous Laplace operator. Common applications include image processing
, where it is known as the Laplace filter, and in machine learning for clustering and semi-supervised learning
on neighborhood graphs.
, differing by sign and scale factor (sometimes one averages over the neighboring vertices, other times one just sums; this makes no difference for a regular graph
). The traditional definition of the graph Laplacian, given below, corresponds to the negative continuous Laplacian on a domain with a free boundary.
Let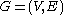
be a graph with vertices 
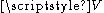and edges 
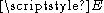. Let 
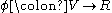be a ring
-valued function
of the vertices. Then, the discrete Laplacian
acting on 
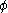is defined by
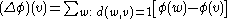
where
is the graph distance
between vertices w and v. Thus, this sum is over the nearest neighbors of the vertex v. For a graph with a finite number of edges and vertices, this definition is identical to that of the Laplacian matrix
. That is,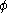
can be written as a column vector; and so 
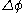is the product of the column vector and the Laplacian matrix, while 
is just the vth entry of the product vector.
If the graph has weighted edges, that is, a weighting function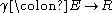
is given, then the definition can be generalized to
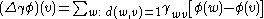
where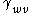
is the weight value on the edge 
.
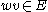Closely related to the discrete Laplacian is the averaging operator:
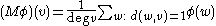
or by the finite element method
can also be called Discrete Laplacians. For example, the Laplacian in two dimensions can be approximated using the five-point stencil
finite difference method
, resulting in
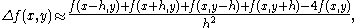
where the grid size is h in both dimensions, so that the five point stencil of a point (x, y) in the grid is
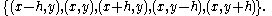
If the grid size h=1, the result is the negative discrete Laplacian on the graph, which is the square lattice grid
. There are no constraints here on the values of the function f(x,y) on the boundary of the lattice grid, thus this is the case of the homogeneous Neumann boundary condition
, i.e., free boundary. Other types of boundary conditions, e.g., the homogeneous Dirichlet boundary condition
, where f(x,y)=0 on the boundary of the grid, are rarely used for graph Laplacians, but are common in other applications.
Multidimensional discrete Laplacians on rectangular cuboid regular grid
s have very special properties, e.g., they are Kronecker sums of one-dimensional discrete Laplacians, see Kronecker sum of discrete Laplacians
, in which case all its eigenvalues and eigenvectors can be explicitly calculated.
with the following kernels:
or, including the diagonals:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the discrete Laplace operator is an analog of the continuous Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, defined so that it has meaning on a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
or a discrete grid
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
. For the case of a finite-dimensional graph (having a finite number of edges and vertices), the discrete Laplace operator is more commonly called the Laplacian matrix
Laplacian matrix
In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...
.
The discrete Laplace operator occurs in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
problems such as the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
and loop quantum gravity
Loop quantum gravity
Loop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
, as well as in the study of discrete dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. It is also used in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
as a stand-in for the continuous Laplace operator. Common applications include image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, where it is known as the Laplace filter, and in machine learning for clustering and semi-supervised learning
Semi-supervised learning
In computer science, semi-supervised learning is a class of machine learning techniques that make use of both labeled and unlabeled data for training - typically a small amount of labeled data with a large amount of unlabeled data...
on neighborhood graphs.
On Graphs
There are various definitions of the discrete Laplacian for graphsGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, differing by sign and scale factor (sometimes one averages over the neighboring vertices, other times one just sums; this makes no difference for a regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
). The traditional definition of the graph Laplacian, given below, corresponds to the negative continuous Laplacian on a domain with a free boundary.
Let
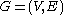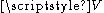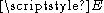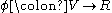be a graph with vertices and edges . Let be a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the vertices. Then, the discrete Laplacian
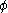acting on is defined by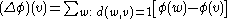where
is the graph distanceDistance (graph theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
between vertices w and v. Thus, this sum is over the nearest neighbors of the vertex v. For a graph with a finite number of edges and vertices, this definition is identical to that of the Laplacian matrix
Laplacian matrix
In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...
. That is,
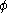can be written as a column vector; and so 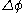is the product of the column vector and the Laplacian matrix, while is just the vth entry of the product vector.If the graph has weighted edges, that is, a weighting function
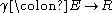is given, then the definition can be generalized to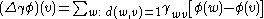where
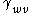is the weight value on the edge 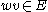.Closely related to the discrete Laplacian is the averaging operator:
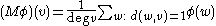
Approximations of the continuous Laplacian
Approximations of the Laplacian, obtained by the finite difference methodFinite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
or by the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
can also be called Discrete Laplacians. For example, the Laplacian in two dimensions can be approximated using the five-point stencil
Five-point stencil
In numerical analysis, given a square grid in one or two dimensions, the five-point stencil of a point in the grid is made up of the point itself together with its four "neighbors"...
finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
, resulting in
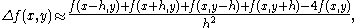
where the grid size is h in both dimensions, so that the five point stencil of a point (x, y) in the grid is
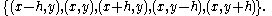
If the grid size h=1, the result is the negative discrete Laplacian on the graph, which is the square lattice grid
Square lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
. There are no constraints here on the values of the function f(x,y) on the boundary of the lattice grid, thus this is the case of the homogeneous Neumann boundary condition
Neumann boundary condition
In mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
, i.e., free boundary. Other types of boundary conditions, e.g., the homogeneous Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
, where f(x,y)=0 on the boundary of the grid, are rarely used for graph Laplacians, but are common in other applications.
Multidimensional discrete Laplacians on rectangular cuboid regular grid
Regular grid
A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
s have very special properties, e.g., they are Kronecker sums of one-dimensional discrete Laplacians, see Kronecker sum of discrete Laplacians
Kronecker sum of discrete Laplacians
In mathematics, the Kronecker sum of discrete Laplacians, named after Leopold Kronecker, is a discrete version of the separation of variables for the continuous Laplacian in a rectangular cuboid domain.-General form of the Kronecker sum of discrete Laplacians:...
, in which case all its eigenvalues and eigenvectors can be explicitly calculated.
Image Processing
Discrete Laplace operator is often used in image processing e.g. in edge detection and motion estimation applications. The discrete Laplacian is defined as the sum of the second derivatives Laplace operator#Coordinate expressions and calculated as sum of differences over the nearest neighbours of the central pixel.Implementation in Image Processing
For one, two and three dimensional signals, the discrete laplacian can be given as convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with the following kernels:
- 1D-filter:
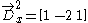
- 2D-filter:
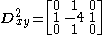
or, including the diagonals:
- 2D-filter:
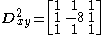
- 3D-filter:
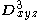is given by: first plane = 
; second plane =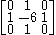 
; third plane =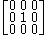 
- D-filter: For the element
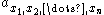of the kernel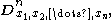 
-
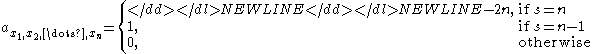
- where is the position (either , or ) of the element in the kernel in the direction, and is the number of directions for which .
These kernels are deduced by using discrete differential quotients.
Spectrum
The spectrum of the discrete Laplacian is of key interest; since it is a self-adjoint operatorSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
, it has a real spectrum. For the convention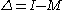
, the spectrum lies within 
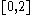(as the averaging operator has spectral values in 
) and contains 0 (for constant functions). The smallest non-zero eigenvalue is denoted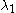 
and is called the spectral gapSpectral gapIn mathematics, the spectral gap is the difference between the moduli of the two largest eigenvalues of a matrix or operator; alternately, it is sometimes taken as the smallest non-zero eigenvalue. Various theorems relate this difference to other properties of the system.See:* Expander graph *...
. There is also the notion of the spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
, commonly taken as the largest eigenvalue.
The eigenvectors don't depend on the convention above (for regular graphRegular graphIn graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
s), and are the same as for the averaging operator (as they differ by adding a multiple of the identity), though the eigenvalues differ according to the convention.
Theorems
If the graph is an infinite square lattice gridSquare latticeIn mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
, then this definition of the Laplacian can be shown to correspond to the continuous Laplacian in the limit of an infinitely fine grid. Thus, for example, on a one-dimensional grid we have
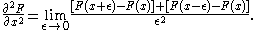
This definition of the Laplacian is commonly used in numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
and in image processingImage processingIn electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
. In image processing, it is considered to be a type of digital filterDigital filterIn electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
, more specifically an edge filter, called the Laplace filter.
Discrete Schrödinger operator
Let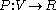
be a potentialPotential*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
function defined on the graph. Note that P can be considered to be a multiplicative operator acting diagonally on
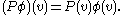
Then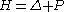
is the discrete Schrödinger operator, an analog of the continuous Schrödinger operatorSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
.
If the number of edges meeting at a vertex is uniformly bounded, and the potential is bounded, then H is bounded and self-adjointSelf-adjointIn mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
.
The spectral properties of this Hamiltonian can be studied with Stone's theorem; this is a consequence of the duality between posets and Boolean algebras.
On regular lattices, the operator typically has both traveling-wave as well as Anderson localizationAnderson localizationIn condensed matter physics, Anderson localization, also known as strong localization, is the absence of diffusion of waves in a disordered medium. This phenomenon is named after the American physicist P. W...
solutions, depending on whether the potential is periodic or random.
Discrete Green's function
The Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
of the discrete Schrödinger operator is given in the resolvent formalismResolvent formalismIn mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
by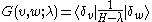
where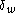
is understood to be the Kronecker delta function on the graph: 
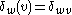; that is, it equals 1 if v=w and 0 otherwise.
For fixe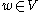d
and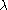 
a complex number, the Green's function considered to be a function of v is the unique solution to
ADE classification
Certain equations involving the discrete Laplacian only have solutions on the simply-laced Dynkin diagrams (all edges multiplicity 1), and are an example of the ADE classificationADE classificationIn mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
. Specifically, the only positive solutions to the homogeneous equation: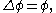
in words,- "Twice any label is the sum of the labels on adjacent vertices,"
are on the extended (affine) ADE Dynkin diagrams, of which there are 2 infinite families (A and D) and 3 exceptions (E). The resulting numbering is unique up to scale, and if the smallest value is set at 1, the other numbers are integers, ranging up to 6.
The ordinary ADE graphs are the only graphs that admit a positive labeling with the following property:- Twice any label minus two is the sum of the labels on adjacent vertices.
In terms of the Laplacian, the positive solutions to the inhomogeneous equation: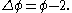
The resulting numbering is unique (scale is specified by the "2"), and consists of integers; for E8 they range from 58 to 270, and have been observed as early as .
External links