
Digital filter
Encyclopedia
Electronics
Electronics is the branch of science, engineering and technology that deals with electrical circuits involving active electrical components such as vacuum tubes, transistors, diodes and integrated circuits, and associated passive interconnection technologies...
, computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a digital filter is a system that performs mathematical operations on a sampled
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
, discrete-time signal
Signal (electrical engineering)
In the fields of communications, signal processing, and in electrical engineering more generally, a signal is any time-varying or spatial-varying quantity....
to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter
Electronic filter
Electronic filters are electronic circuits which perform signal processing functions, specifically to remove unwanted frequency components from the signal, to enhance wanted ones, or both...
, the analog filter, which is an electronic circuit
Electronic circuit
An electronic circuit is composed of individual electronic components, such as resistors, transistors, capacitors, inductors and diodes, connected by conductive wires or traces through which electric current can flow...
operating on continuous-time analog signal
Analog signal
An analog or analogue signal is any continuous signal for which the time varying feature of the signal is a representation of some other time varying quantity, i.e., analogous to another time varying signal. It differs from a digital signal in terms of small fluctuations in the signal which are...
s. An analog signal may be processed by a digital filter by first being digitized and represented as a sequence of numbers, then manipulated mathematically, and then reconstructed as a new analog signal (see digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
). In an analog filter, the input signal is "directly" manipulated by the circuit.
A digital filter system usually consists of an analog-to-digital converter
Analog-to-digital converter
An analog-to-digital converter is a device that converts a continuous quantity to a discrete time digital representation. An ADC may also provide an isolated measurement...
to sample the input signal, followed by a microprocessor and some peripheral components such as memory to store data and filter coefficients etc. Finally a digital-to-analog converter
Digital-to-analog converter
In electronics, a digital-to-analog converter is a device that converts a digital code to an analog signal . An analog-to-digital converter performs the reverse operation...
to complete the output stage. Program Instructions (software) running on the microprocessor implement the digital filter by performing the necessary mathematical operations on the numbers received from the ADC. In some high performance applications, an FPGA or ASIC
ASIC
ASIC may refer to:* Application-specific integrated circuit, an integrated circuit developed for a particular use, as opposed to a customised general-purpose device.* ASIC programming language, a dialect of BASIC...
is used instead of a general purpose microprocessor, or a specialized DSP with specific paralleled architecture for expediting operations such as filtering.
Digital filters may be more expensive than an equivalent analog filter due to their increased complexity, but they make practical many designs that are impractical or impossible as analog filters. Since digital filters use a sampling process and discrete-time processing, they experience latency (the difference in time between the input and the response), which is almost irrelevant in analog filters.
Digital filters are commonplace and an essential element of everyday electronics such as radio
Radio
Radio is the transmission of signals through free space by modulation of electromagnetic waves with frequencies below those of visible light. Electromagnetic radiation travels by means of oscillating electromagnetic fields that pass through the air and the vacuum of space...
s, cellphones, and stereo receivers
Stereophonic sound
The term Stereophonic, commonly called stereo, sound refers to any method of sound reproduction in which an attempt is made to create an illusion of directionality and audible perspective...
.
Characterization of digital filters
A digital filter is characterized by its transfer functionTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
, or equivalently, its difference equation. Mathematical analysis of the transfer function can describe how it will respond to any input. As such, designing a filter consists of developing specifications appropriate to the problem (for example, a second-order low pass filter with a specific cut-off frequency), and then producing a transfer function which meets the specifications.
The transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
for a linear, time-invariant, digital filter can be expressed as a transfer function in the Z-domain
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
; if it is causal, then it has the form:
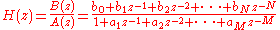
where the order of the filter is the greater of N or M.
See Z-transform's LCCD equation for further discussion of this transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
.
This is the form for a recursive filter
Recursive filter
In signal processing, a recursive filter is a type of filter which re-uses one or more of its outputs as an input. This feedback typically results in an unending impulse response , characterised by either exponentially growing, decaying, or sinusoidal signal output components.However, a recursive...
with both the inputs (Numerator) and outputs (Denominator), which typically leads to an IIR infinite impulse response
Infinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
behaviour, but if the denominator is made equal to unity i.e. no feedback, then this becomes an FIR or finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
filter.
Analysis techniques
A variety of mathematical techniques may be employed to analyze the behaviour of a given digital filter. Many of these analysis techniques may also be employed in designs, and often form the basis of a filter specification.Typically, one analyzes filters by calculating how the filter will respond to a simple input such as an impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
. One can then extend this information to visualize the filter's response to more complex signals. Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
s have been used, together with digital video
Digital video
Digital video is a type of digital recording system that works by using a digital rather than an analog video signal.The terms camera, video camera, and camcorder are used interchangeably in this article.- History :...
, for this purpose.
Impulse response
The impulse responseImpulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
, often denoted
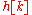 or
or 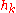 , is a measurement of how a filter will respond to the Kronecker delta function. For example, given a difference equation, one would set
, is a measurement of how a filter will respond to the Kronecker delta function. For example, given a difference equation, one would set  and
and  for
for 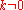 and evaluate. The impulse response is a characterization of the filter's behaviour. Digital filters are typically considered in two categories: infinite impulse response
and evaluate. The impulse response is a characterization of the filter's behaviour. Digital filters are typically considered in two categories: infinite impulse responseInfinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
(IIR) and finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
(FIR).
In the case of linear time-invariant FIR filters, the impulse response is exactly equal to the sequence of filter coefficients:
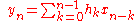
IIR filters on the other hand are recursive, with the output depending on both current and previous inputs as well as previous outputs. The general form of the an IIR filter is thus:
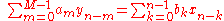
Plotting the impulse response will reveal how a filter will respond to a sudden, momentary disturbance.
Difference equation
In discrete-time systems, the digital filter is often implemented by converting the transfer functionTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
to a linear constant-coefficient difference equation (LCCD) via the Z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
. The discrete frequency-domain transfer function is written as the ratio of two polynomials. For example:
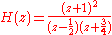
This is expanded:
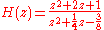
and divided by the highest order of
 :
: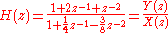
The coefficients of the denominator,
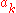 , are the 'feed-backward' coefficients and the coefficients of the numerator are the 'feed-forward' coefficients,
, are the 'feed-backward' coefficients and the coefficients of the numerator are the 'feed-forward' coefficients, 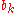 . The resultant linear difference equation is:
. The resultant linear difference equation is: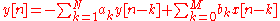
or, for the example above:
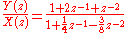
rearranging terms:
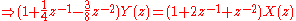
then by taking the inverse z-transform:
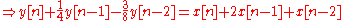
and finally, by solving for
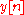 :
: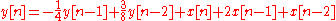
This equation shows how to compute the next output sample,
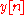 , in terms of the past outputs,
, in terms of the past outputs, 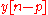 , the present input,
, the present input, 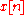 , and the past inputs,
, and the past inputs, 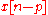 . Applying the filter to an input in this form is equivalent to a Direct Form I or II realization, depending on the exact order of evaluation.
. Applying the filter to an input in this form is equivalent to a Direct Form I or II realization, depending on the exact order of evaluation.Filter design
The design of digital filters is a deceptively complex topic. Although filters are easily understood and calculated, the practical challenges of their design and implementation are significant and are the subject of much advanced research.There are two categories of digital filter: the recursive filter
Recursive filter
In signal processing, a recursive filter is a type of filter which re-uses one or more of its outputs as an input. This feedback typically results in an unending impulse response , characterised by either exponentially growing, decaying, or sinusoidal signal output components.However, a recursive...
and the nonrecursive filter. These are often referred to as infinite impulse response
Infinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
(IIR) filters and finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
(FIR) filters, respectively.
Filter realization
After a filter is designed, it must be realized by developing a signal flow diagram that describes the filter in terms of operations on sample sequences.A given transfer function may be realized in many ways. Consider how a simple expression such as
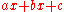 could be evaluated – one could also compute the equivalent
could be evaluated – one could also compute the equivalent  . In the same way, all realizations may be seen as "factorizations" of the same transfer function, but different realizations will have different numerical properties. Specifically, some realizations are more efficient in terms of the number of operations or storage elements required for their implementation, and others provide advantages such as improved numerical stability and reduced round-off error. Some structures are better for fixed-point arithmetic
. In the same way, all realizations may be seen as "factorizations" of the same transfer function, but different realizations will have different numerical properties. Specifically, some realizations are more efficient in terms of the number of operations or storage elements required for their implementation, and others provide advantages such as improved numerical stability and reduced round-off error. Some structures are better for fixed-point arithmeticFixed-point arithmetic
In computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits after the radix point...
and others may be better for floating-point arithmetic.
Direct Form I
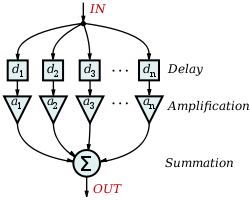
A straightforward approach for IIR filter realization is Direct Form I, where the difference equation is evaluated directly. This form is practical for small filters, but may be inefficient and impractical (numerically unstable) for complex designs. In general, this form requires 2N delay elements (for both input and output signals) for a filter of order N.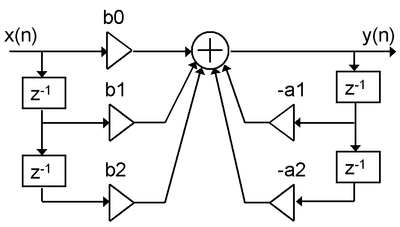
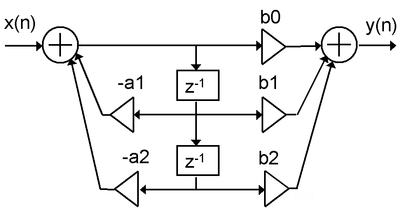
Direct Form II
The alternate Direct Form II only needs N delay units, where N is the order of the filter – potentially half as much as Direct Form I. This structure is obtained by reversing the order of the numerator and denominator sections of Direct Form I, since they are in fact two linear systems, and the commutativity property applies. Then, one will notice that there are two columns of delays (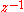 ) that tap off the center net, and these can be combined since they are redundant, yielding the implementation as shown below.
) that tap off the center net, and these can be combined since they are redundant, yielding the implementation as shown below.The disadvantage is that Direct Form II increases the possibility of arithmetic overflow for filters of high Q or resonance. It has been shown that as Q increases, the round-off noise of both direct form topologies increases without bounds. This is because, conceptually, the signal is first passed through an all-pole filter (which normally boosts gain at the resonant frequencies) before the result of that is saturated, then passed through an all-zero filter (which often attenuates much of what the all-pole half amplifies).
Cascaded second-order sections
A common strategy is to realize a higher-order (greater than 2) digital filter as a cascaded series of second-order "biquadratric" (or "biquad") sections (see digital biquad filter). Advantages of this strategy is that the coefficient range is limited. Cascading direct form II sections result in N delay elements for filter order of N. Cascading direct form I sections result in N+2 delay elements since the delay elements of the input of any section (except the first section) are a redundant with the delay elements of the output of the preceding section.Other Forms
Other forms include:- Direct Form I and II transpose
- Series/cascade
- Parallel
- Ladder form
- Lattice form
- Coupled normal form
- Multifeedback
- Analog-inspired forms such as Sallen-key and state variable filters
- Systolic arrays
Comparison of analog and digital filters
Digital filters are not subject to the component non-linearities that greatly complicate the design of analog filters. Analog filters consist of imperfect electronic components, whose values are specified to a limit tolerance (e.g. resistor values often have a tolerance of +/- 5%) and which may also change with temperature and drift with time. As the order of an analog filter increases, and thus its component count, the effect of variable component errors is greatly magnified. In digital filters, the coefficient values are stored in computer memory, making them far more stable and predictable.Because the coefficients of digital filters are definite, they can be used to achieve much more complex and selective designs – specifically with digital filters, one can achieve a lower passband ripple, faster transition, and higher stopband attenuation than is practical with analog filters. Even if the design could be achieved using analog filters, the engineering cost of designing an equivalent digital filter would likely be much lower. Furthermore, one can readily modify the coefficients of a digital filter to make an adaptive filter
Adaptive filter
An adaptive filter is a filter that self-adjusts its transfer function according to an optimization algorithm driven by an error signal. Because of the complexity of the optimization algorithms, most adaptive filters are digital filters. By way of contrast, a non-adaptive filter has a static...
or a user-controllable parametric filter. While these techniques are possible in an analog filter, they are again considerably more difficult.
Digital filters can be used in the design of finite impulse response filters. Analog filters do not have the same capability, because finite impulse response filters require delay elements.
Digital filters rely less on analog circuitry, potentially allowing for a better signal-to-noise ratio
Signal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
. A digital filter will introduce noise to a signal during analog low pass filtering, analog to digital conversion, digital to analog conversion and may introduce digital noise due to quantization. With analog filters, every component is a source of thermal noise (such as Johnson noise), so as the filter complexity grows, so does the noise.
However, digital filters do introduce a higher fundamental latency to the system. In an analog filter, latency is often negligible; strictly speaking it is the time for an electrical signal to propagate through the filter circuit. In digital filters, latency is a function of the number of delay elements in the system.
Digital filters also tend to be more limited in bandwidth than analog filters. High bandwidth digital filters require expensive ADC/DACs and fast computer hardware for processing.
In very simple cases, it is more cost effective to use an analog filter. Introducing a digital filter requires considerable overhead circuitry, as previously discussed, including two low pass analog filters.
Types of digital filters
Many digital filters are based on the Fast Fourier transformFast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
, a mathematical algorithm that quickly extracts the frequency spectrum
Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
of a signal, allowing the spectrum to be manipulated (such as to create band-pass filters) before converting the modified spectrum back into a time-series signal.
Another form of a digital filter is that of a state-space
State space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
model.
A well used state-space filter is the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
published by Rudolf Kalman
Rudolf Kalman
Rudolf Emil Kálmán is a Hungarian-American electrical engineer, mathematical system theorist, and college professor, who was educated in the United States, and has done most of his work there. He is currently a retired professor from three different institutes of technology and universities...
in 1960.
See also
- Bessel filterBessel filterIn electronics and signal processing, a Bessel filter is a type of linear filter with a maximally flat group delay . Bessel filters are often used in audio crossover systems...
- Butterworth filterButterworth filterThe Butterworth filter is a type of signal processing filter designed to have as flat a frequency response as possible in the passband so that it is also termed a maximally flat magnitude filter...
- Elliptical filter (Cauer filter)
- Linkwitz-Riley filterLinkwitz-Riley filterA Linkwitz–Riley filter is an infinite impulse response filter used in Linkwitz–Riley audio crossovers, named after its inventors Siegfried Linkwitz and Russ Riley, which was originally described in Passive Crossover Networks for Noncoincident Drivers in . It is also known as a Butterworth squared...
- Chebyshev filterChebyshev filterChebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
- Ladder filter
- Sample (signal)
- Electronic filterElectronic filterElectronic filters are electronic circuits which perform signal processing functions, specifically to remove unwanted frequency components from the signal, to enhance wanted ones, or both...
- Filter designFilter designFilter design is the process of designing a filter , often a linear shift-invariant filter, that satisfies a set of requirements, some of which are contradictory...
- Biquad filter
- High-pass filterHigh-pass filterA high-pass filter is a device that passes high frequencies and attenuates frequencies lower than its cutoff frequency. A high-pass filter is usually modeled as a linear time-invariant system...
, Low-pass filterLow-pass filterA low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter... - Infinite impulse responseInfinite impulse responseInfinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
, Finite impulse responseFinite impulse responseA finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely... - Bilinear transformBilinear transformThe bilinear transform is used in digital signal processing and discrete-time control theory to transform continuous-time system representations to discrete-time and vice versa....
General
- A. Antoniou, Digital Filters: Analysis, Design, and Applications, New York, NY: McGraw-Hill, 1993.
- J. O. Smith III, Introduction to Digital Filters with Audio Applications, Center for Computer Research in Music and Acoustics (CCRMA), Stanford University, September 2007 Edition.
- S.K. Mitra, Digital Signal Processing: A Computer-Based Approach, New York, NY: McGraw-Hill, 1998.
- A.V. Oppenheim and R.W. Schafer, Discrete-Time Signal Processing, Upper Saddle River, NJ: Prentice-Hall, 1999.
- J.F. Kaiser, Nonrecursive Digital Filter Design Using the Io-sinh Window Function, Proc. 1974 IEEE Int. Symp. Circuit Theory, pp. 20–23, 1974.
- S.W.A. Bergen and A. Antoniou, Design of Nonrecursive Digital Filters Using the Ultraspherical Window Function, EURASIP Journal on Applied Signal Processing, vol. 2005, no. 12, pp. 1910–1922, 2005.
- T.W. ParksThomas W. ParksThomas W. Parks is an American electrical engineer and Professor Emeritus of Electrical and Computer Engineering at Cornell University. He is best known for his contributions to digital signal processing, especially digital filter design and computation of the fast Fourier transform...
and J.H. McClellanJames H. McClellanJames H. McClellan is the Byers Professor of Signal Processing at the Georgia Institute of Technology. He is widely known for his creation of the McClellan transform and for his co-authorship of the Parks-McClellan filter design algorithm.- Education :...
, Chebyshev Approximation for Nonrecursive Digital Filters with Linear Phase, IEEE Trans. Circuit Theory, vol. CT-19, pp. 189–194, Mar. 1972. - L. R. Rabiner, J.H. McClellan, and T.W. Parks, FIR Digital Filter Design Techniques Using Weighted Chebyshev Approximation, Proc. IEEE, vol. 63, pp. 595–610, Apr. 1975.
- A.G. Deczky, Synthesis of Recursive Digital Filters Using the Minimum p-Error Criterion, IEEE Trans. Audio Electroacoust., vol. AU-20, pp. 257–263, Oct. 1972.
External links
- WinFilter – Free filter design software
- Filtplot – Free customizable digital filter design software built with python and boost (WinXP/Ubuntu 6.10/RHEL-4). Also with interactive web interface.
- DISPRO – Free filter design software
- Java demonstration of digital filters
- IIR Explorer educational software
- Introduction to Filtering
- Introduction to Digital Filters
- Publicly available, very comprehensive lecture notes on Digital Linear Filtering (see bottom of the page)

