Laplacian matrix
Encyclopedia
In the mathematical
field of graph theory
the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix
representation of a graph
. Together with Kirchhoff's theorem
it can be used to calculate the number of spanning tree
s for a given graph. The Laplacian matrix can be used to find many other properties of the graph, see spectral graph theory
. Cheeger's inequality from Riemannian Geometry has a discrete analogue involving the Laplacian Matrix, this is perhaps the most important theorem in Spectral Graph theory and one of the most useful facts in algorithmic applications. It approximates the sparsest cut of a graph through the second eigenvalue of its Laplacian.
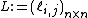is defined as:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
representation of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. Together with Kirchhoff's theorem
Kirchhoff's theorem
In the mathematical field of graph theory Kirchhoff's theorem or Kirchhoff's matrix tree theorem named after Gustav Kirchhoff is a theorem about the number of spanning trees in a graph...
it can be used to calculate the number of spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
s for a given graph. The Laplacian matrix can be used to find many other properties of the graph, see spectral graph theory
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
. Cheeger's inequality from Riemannian Geometry has a discrete analogue involving the Laplacian Matrix, this is perhaps the most important theorem in Spectral Graph theory and one of the most useful facts in algorithmic applications. It approximates the sparsest cut of a graph through the second eigenvalue of its Laplacian.
Definition
Given a simple graph G with n vertices, its Laplacian matrix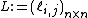 is defined as:-
That is, it is the difference of the degree matrixDegree matrixIn the mathematical field of graph theory the degree matrix is a diagonal matrix which contains information about the degree of each vertex. It is used together with the adjacency matrix to construct the Laplacian matrix of a graph.-Definition:...
and the adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of the graph.
In the case of directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s, either the indegree or outdegreeDegree (graph theory)In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
might be used, depending on the application.
The normalized Laplacian matrix is defined as:
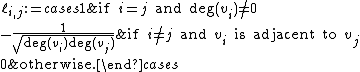
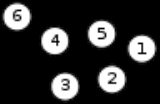
Example
Here is a simple example of a labeled graph and its Laplacian matrix.
Labeled graph Laplacian matrix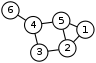 
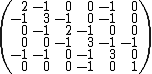
Properties
For a graph G and its Laplacian matrix L with eigenvalues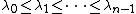
:
- L is always positive-semidefinitePositive-definite matrixIn linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
(
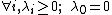). - The number of times 0 appears as an eigenvalue in the Laplacian is the number of connected componentsConnected component (graph theory)In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
in the graph. -
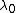is always 0 because every Laplacian matrix has an eigenvector of 
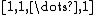that, for each row, adds the corresponding node's degree to a "-1" for each neighbor, thereby producing zero by definition. -
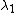is called the algebraic connectivityAlgebraic connectivityThe algebraic connectivity of a graph G is the second-smallest eigenvalue of the Laplacian matrix of G. This eigenvalue is greater than 0 if and only if G is a connected graph. This is a corollary to the fact that the number of times 0 appears as an eigenvalue in the Laplacian is the number of...
. - The smallest non-zero eigenvalue of L is called the spectral gapExpander graphIn combinatorics, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion as described below...
. - The second smallest eigenvalue of L is the algebraic connectivityAlgebraic connectivityThe algebraic connectivity of a graph G is the second-smallest eigenvalue of the Laplacian matrix of G. This eigenvalue is greater than 0 if and only if G is a connected graph. This is a corollary to the fact that the number of times 0 appears as an eigenvalue in the Laplacian is the number of...
(or Fiedler value) of G.
If we define a signed edge adjacency matrix M with element Mev for edge e (connecting vertex i and j, with i < j) and vertex v given by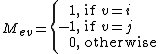
then the Laplacian matrix L satisifies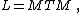
where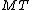
is the matrix transposeTransposeIn linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of M.
Deformed Laplacian
The deformed Laplacian is commonly defined as
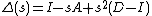
where I is the unit matrix, A is the adjacency matrix, and D is the degree matrix, and s is a (complex-valued) number. Note that normal Laplacian is just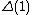
.
As a matrix representation of the negative discrete Laplace operator
The Laplacian matrix can be interpreted as a matrix representation of a particular case of the negative discrete Laplace operatorDiscrete Laplace operatorIn mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
Discrete Laplace operatorIn mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
. Such an interpretation allows one, e.g., to generalise the Laplacian matrix to the case of graphs with an infinite number of vertices and edges, leading to a Laplacian matrix of an infinite size.
As an approximation to the negative continuous Laplacian
The graph Laplacian matrix can be further viewed as a matrix form of an approximation to the negative Laplacian operator obtained by the finite difference methodFinite difference methodIn mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
. In this interpretation, every graph vertex is treated as a grid point, the local connectivity of the vertex determines the finite difference approximation stencilFinite difference methodIn mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
at this grid point, the grid size is always one for every edge, and there are no constraints in any grid points, which corresponds the case of the homogeneous Neumann boundary conditionNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
, i.e., free boundary. - L is always positive-semidefinite