.gif)
Kernel (statistics)
Encyclopedia
A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation
to estimate random variable
s' density functions, or in kernel regression
to estimate the conditional expectation
of a random variable. Kernels are also used in time-series, in the use of the periodogram
to estimate the spectral density
. An additional use is in the estimation of a time-varying intensity for a point process
.
Commonly, kernel widths must also be specified when running a non-parametric estimation.
The first requirement ensures that the method of kernel density estimation results in a probability density function
. The second requirement ensures that the average of the corresponding distribution is equal to that of the sample used.
If K is a kernel, then so is the function K* defined by K*(u) = λ−1K(λ−1u), where λ > 0. This can be used to select a scale that is appropriate for the data.
In the table below, 1{…} is the indicator function.
{| class="wikitable" style="background-color:white;text-align:left"
!colspan=3| Kernel Functions, K(u)
!
!
|-
! Uniform
|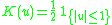
|
|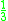
|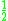
|-
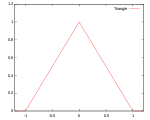
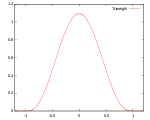
! Triangular
|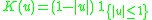
|
|
|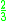
|-
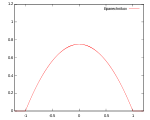
! Epanechnikov
|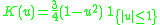
|
|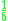
|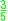
|-
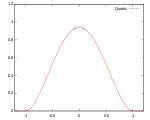
! Quartic
(biweight)
|
|
|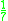
|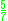
|-
! Triweight
|
|
|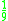
|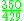
|-
! Tricube
|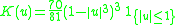
|
|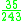
|
|-
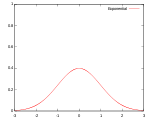
! Gaussian
|
|
|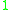
|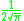
|-
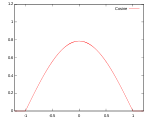
! Cosine
|
|
|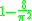
|
|}
Kernel density estimation
In statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...
to estimate random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s' density functions, or in kernel regression
Kernel regression
The kernel regression is a non-parametric technique in statistics to estimate the conditional expectation of a random variable. The objective is to find a non-linear relation between a pair of random variables X and Y....
to estimate the conditional expectation
Conditional expectation
In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
of a random variable. Kernels are also used in time-series, in the use of the periodogram
Periodogram
The periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
to estimate the spectral density
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
. An additional use is in the estimation of a time-varying intensity for a point process
Point process
In statistics and probability theory, a point process is a type of random process for which any one realisation consists of a set of isolated points either in time or geographical space, or in even more general spaces...
.
Commonly, kernel widths must also be specified when running a non-parametric estimation.
Definition
A kernel is a non-negative real-valued integrable function K satisfying the following two requirements:The first requirement ensures that the method of kernel density estimation results in a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
. The second requirement ensures that the average of the corresponding distribution is equal to that of the sample used.
If K is a kernel, then so is the function K* defined by K*(u) = λ−1K(λ−1u), where λ > 0. This can be used to select a scale that is appropriate for the data.
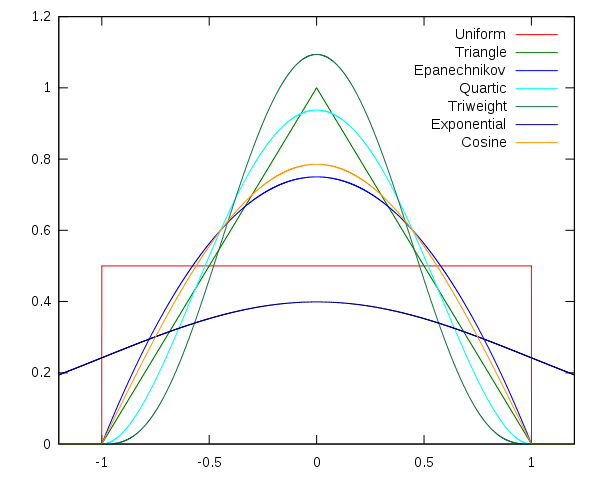
Kernel functions in common use
Several types of kernel functions are commonly used: uniform, triangle, Epanechnikov, quartic (biweight), tricube, triweight, Gaussian, and cosine.In the table below, 1{…} is the indicator function.
{| class="wikitable" style="background-color:white;text-align:left"
!colspan=3| Kernel Functions, K(u)
!

!

|-
! Uniform
|
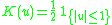
|

|
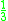
|
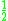
|-
! Triangular
|
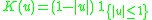
|

|

|
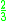
|-
! Epanechnikov
|
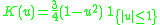
|

|
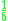
|
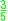
|-
! Quartic
(biweight)
|

|

|
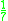
|
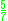
|-
! Triweight
|

|

|
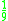
|
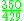
|-
! Tricube
|
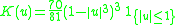
|
|
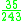
|
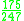
|-
! Gaussian
|

|

|
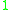
|
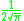
|-
! Cosine
|

|

|
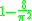
|

|}
All of the above Kernels in a Common Coordinate System

See also
- Kernel density estimationKernel density estimationIn statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...
- Kernel smootherKernel smootherA kernel smoother is a statistical technique for estimating a real valued function f\,\,\left by using its noisy observations, when no parametric model for this function is known...
- Stochastic kernelStochastic kernelIn statistics, a stochastic kernel estimate is an estimate of the transition function of a stochastic process. Often, this is an estimate of the conditional density function obtained using kernel density estimation...
- Density estimationDensity estimationIn probability and statistics,density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function...



