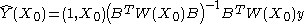Kernel smoother
Encyclopedia
A kernel smoother is a statistical
technique for estimating a real valued function
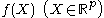 by using its noisy observations, when no parametric model
by using its noisy observations, when no parametric model
for this function is known. The estimated function is smooth, and the level of smoothness is set by a single parameter.
This technique is most appropriate for low dimensional (p < 3) data visualization purposes. Actually, the kernel smoother represents the set of irregular data points as a smooth line or surface.
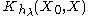 be a kernel defined by
be a kernel defined by
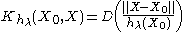
where:
Popular kernels
used for smoothing include
Let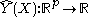 be a continuous function of X. For each
be a continuous function of X. For each 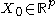 , the Nadaraya-Watson kernel-weighted average (smooth Y(X) estimation) is defined by
, the Nadaraya-Watson kernel-weighted average (smooth Y(X) estimation) is defined by
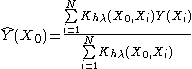
where:
In the following sections, we describe some particular cases of kernel smoothers.
smoother is the following. For each point X0, take m nearest neighbors and estimate the value of Y(X0) by averaging the values of these neighbors.
Formally,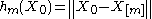 , where
, where 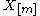 is the mth closest to X0 neighbor, and
is the mth closest to X0 neighbor, and
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
technique for estimating a real valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
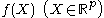 by using its noisy observations, when no parametric model
by using its noisy observations, when no parametric modelNon-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
for this function is known. The estimated function is smooth, and the level of smoothness is set by a single parameter.
This technique is most appropriate for low dimensional (p < 3) data visualization purposes. Actually, the kernel smoother represents the set of irregular data points as a smooth line or surface.
Definitions
Let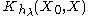 be a kernel defined by
be a kernel defined by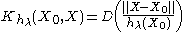
where:
-
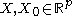
-
 is the Euclidean norm
is the Euclidean norm -
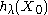 is a parameter (kernel radius)
is a parameter (kernel radius) - D(t) typically is a positive real valued function, which value is decreasing (or not increasing) for the increasing distance between the X and X0.
Popular kernels
Kernel (statistics)
A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...
used for smoothing include
- Epanechnikov
- Tri-cube
- Gaussian
Let
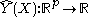 be a continuous function of X. For each
be a continuous function of X. For each 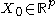 , the Nadaraya-Watson kernel-weighted average (smooth Y(X) estimation) is defined by
, the Nadaraya-Watson kernel-weighted average (smooth Y(X) estimation) is defined by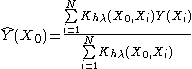
where:
- N is the number of observed points
- Y(Xi) are the observations at Xi points.
In the following sections, we describe some particular cases of kernel smoothers.
Nearest neighbor smoother
The idea of the nearest neighborK-nearest neighbor algorithm
In pattern recognition, the k-nearest neighbor algorithm is a method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until...
smoother is the following. For each point X0, take m nearest neighbors and estimate the value of Y(X0) by averaging the values of these neighbors.
Formally,
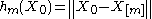 , where
, where 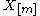 is the mth closest to X0 neighbor, and
is the mth closest to X0 neighbor, and-
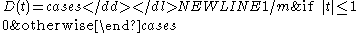
Example:
In this example, X is one-dimensional. For each X0, the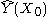 is an average value of 16 closest to X0 points (denoted by red). The result is not smooth enough.
is an average value of 16 closest to X0 points (denoted by red). The result is not smooth enough.
Kernel average smoother
The idea of the kernel average smoother is the following. For each data point X0, choose a constant distance size λ (kernel radius, or window width for p = 1 dimension), and compute a weighted average for all data points that are closer than to X0 (the closer to X0 points get higher weights).
to X0 (the closer to X0 points get higher weights).
Formally, and D(t) is one of the popular kernels.
and D(t) is one of the popular kernels.
Example:
For each X0 the window width is constant, and the weight of each point in the window is schematically denoted by the yellow figure in the graph. It can be seen that the estimation is smooth, but the boundary points are biased. The reason for that is the non-equal number of points (from the right and from the left to the X0) in the window, when the X0 is close enough to the boundary.
Local linear regression
In the two previous sections we assumed that the underlying Y(X) function is locally constant, therefore we were able to use the weighted average for the estimation. The idea of local linear regression is to fit locally a straight line (or a hyperplane for higher dimensions), and not the constant (horizontal line). After fitting the line, the estimation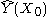 is provided by the value of this line at X0 point. By repeating this procedure for each X0, one can get the estimation function
is provided by the value of this line at X0 point. By repeating this procedure for each X0, one can get the estimation function 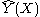 .
.
Like in previous section, the window width is constant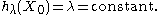
Formally, the local linear regression is computed by solving a weighted least square problem.
For one dimension (p = 1):
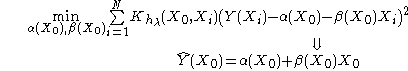
The closed form solution is given by:
where:-

-
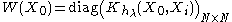
-
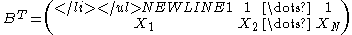
Example:
The resulting function is smooth, and the problem with the biased boundary points is solved.
Local polynomial regression
Instead of fitting locally linear functions, one can fit polynomial functions.
For p=1, one should minimize:
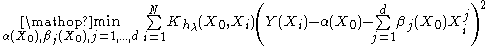
with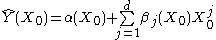
In general case (p>1), one should minimize:
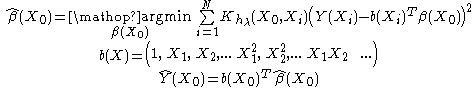
See also
- Kernel (statistics)Kernel (statistics)A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...
- Kernel methodsKernel methodsIn computer science, kernel methods are a class of algorithms for pattern analysis, whose best known elementis the support vector machine...
- Kernel density estimationKernel density estimationIn statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...
- Kernel regressionKernel regressionThe kernel regression is a non-parametric technique in statistics to estimate the conditional expectation of a random variable. The objective is to find a non-linear relation between a pair of random variables X and Y....
- Local regressionLocal regressionLOESS, or LOWESS , is one of many "modern" modeling methods that build on "classical" methods, such as linear and nonlinear least squares regression. Modern regression methods are designed to address situations in which the classical procedures do not perform well or cannot be effectively applied...
- Kernel (statistics)
-