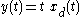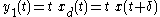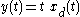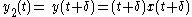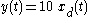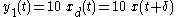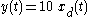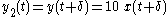A time-invariant system is one whose output does not depend explicitly on time.

If the input signal 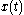produces an output 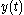then any time shifted input, , results in a time-shifted output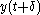

This property can be satisfied if the transfer function

Transfer function

A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...

 of the system is not a function of time except expressed by the input and output.
This property can also be stated in another way in terms of a schematic

If a system is time-invariant then the system block is commutative with an arbitrary delay.

To demonstrate how to determine if a system is time-invariant then consider the two systems:

• System A:
• System B:

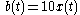
Since system A explicitly depends on t outside of and then it is time-variant.

Time-variant system

A time-variant system is a system that is not time invariant . Roughly speaking, characteristics of its output depend explicitly upon time.- Overview :...

  System B, however, does not depend explicitly on t so it is time-invariant.
A more formal proof of why system A & B from above differ is now presented.
To perform this proof, the second definition will be used.

System A:

Start with a delay of the input

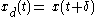
Now delay the output by

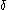
Clearly 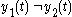, therefore the system is not time-invariant.

System B:

Start with a delay of the input

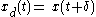
Now delay the output by

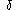
Clearly 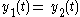, therefore the system is time-invariant.