
Moving average model
Encyclopedia
In time series analysis, the moving-average (MA) model is a common approach for modeling univariate time series models. The notation MA(q) refers to the moving average model of order q:
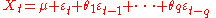
where μ is the mean of the series, the θ1, ..., θq are the parameters of the model and the εt, εt−1,... are white noise
error terms. The value of q is called the order of the MA model.
That is, a moving-average model is conceptually a linear regression
of the current value of the series against previous (unobserved) white noise error terms or random shocks. The random shocks at each point are assumed to come from the same distribution, typically a normal distribution, with location at zero and constant scale. The distinction in this model is that these random shocks are propagated to future values of the time series. Fitting the MA estimates is more complicated than with autoregressive model
s (AR models) because the error terms are not observable. This means that iterative non-linear fitting procedures need to be used in place of linear least squares. MA models also have a less obvious interpretation than AR models.
Sometimes the autocorrelation function (ACF) and partial autocorrelation function
(PACF) will suggest that a MA model would be a better model choice and sometimes both AR and MA terms should be used in the same model (see Box-Jenkins
).
Note, however, that the error terms after the model is fit should be independent and follow the standard assumptions for a univariate process: random drawings from a fixed distribution with the distribution having fixed location and with the distribution having fixed variation.
The moving-average model is essentially a finite impulse response
filter with some additional interpretation placed on it.
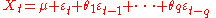
where μ is the mean of the series, the θ1, ..., θq are the parameters of the model and the εt, εt−1,... are white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
error terms. The value of q is called the order of the MA model.
That is, a moving-average model is conceptually a linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
of the current value of the series against previous (unobserved) white noise error terms or random shocks. The random shocks at each point are assumed to come from the same distribution, typically a normal distribution, with location at zero and constant scale. The distinction in this model is that these random shocks are propagated to future values of the time series. Fitting the MA estimates is more complicated than with autoregressive model
Autoregressive model
In statistics and signal processing, an autoregressive model is a type of random process which is often used to model and predict various types of natural phenomena...
s (AR models) because the error terms are not observable. This means that iterative non-linear fitting procedures need to be used in place of linear least squares. MA models also have a less obvious interpretation than AR models.
Sometimes the autocorrelation function (ACF) and partial autocorrelation function
Partial autocorrelation function
In time series analysis, the partial autocorrelation function plays an important role in data analyses aimed at identifying the extent of the lag in an autoregressive model...
(PACF) will suggest that a MA model would be a better model choice and sometimes both AR and MA terms should be used in the same model (see Box-Jenkins
Box-Jenkins
In time series analysis, the Box–Jenkins methodology, named after the statisticians George Box and Gwilym Jenkins, applies autoregressive moving average ARMA or ARIMA models to find the best fit of a time series to past values of this time series, in order to make forecasts.-Modeling approach:The...
).
Note, however, that the error terms after the model is fit should be independent and follow the standard assumptions for a univariate process: random drawings from a fixed distribution with the distribution having fixed location and with the distribution having fixed variation.
The moving-average model is essentially a finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
filter with some additional interpretation placed on it.

