Autoregressive model
Encyclopedia
In statistics
and signal processing
, an autoregressive (AR) model is a type of random process which is often used to model and predict various types of natural phenomena. The autoregressive model is one of a group of linear prediction
formulas that attempt to predict an output of a system based on the previous outputs.
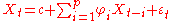
where
are the parameters of the model, 
is a constant (often omitted for simplicity) and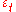 
is white noise
.
An autoregressive model can thus be viewed as the output of an all-pole infinite impulse response
filter whose input is white noise.
Some constraints are necessary on the values of the parameters of this model in order that the model remains wide-sense stationary. For example, processes in the AR(1) model with |φ1| ≥ 1 are not stationary. More generally, for an AR(p) model to be wide-sense stationary, the roots of the polynomial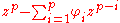
must lie within the unit circle
, i.e., each root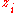
must satisfy 
.
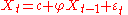
where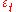
is a white noise process with zero mean and variance 
.
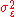(Note: The subscript on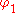
has been dropped.) The process is wide-sense stationary if 
since it is obtained as the output of a stable filter whose input is white noise. (If 
then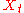 
has infinite variance, and is therefore not wide sense stationary.) Consequently, assuming 
, the mean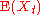 
is identical for all values of t. If the mean is denoted by 
, it follows from
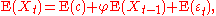
that
and hence
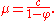
In particular, if
, then the mean is 0.
The variance
is
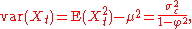
where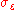
is the standard deviation of 
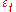. This can be shown by noting that
and then by noticing that the quantity above is a stable fixed point of this relation.
The autocovariance
is given by
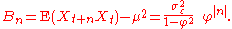
It can be seen that the autocovariance function decays with a decay time (also called time constant
) of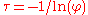
[to see this, write 
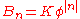where 
is independent of 
. Then note that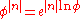 
and match this to the exponential decay law 
].
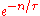The spectral density
function is the Fourier transform
of the autocovariance function. In discrete terms this will be the discrete-time Fourier transform:
This expression is periodic due to the discrete nature of the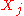
, which is manifested as the cosine term in the denominator. If we assume that the sampling time (
) is much smaller than the decay time (
), then we can use a continuum approximation to 
:
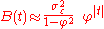
which yields a Lorentzian profile
for the spectral density:
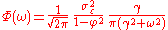
where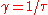
is the angular frequency associated with the decay time 
.
An alternative expression for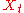
can be derived by first substituting 
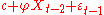for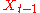 
in the defining equation. Continuing this process N times yields
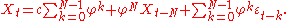
For N approaching infinity,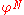
will approach zero and:
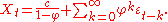
It is seen that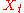
is white noise convolved with the 
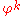kernel plus the constant mean. If the white noise 
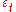is a Gaussian process
then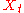
is also a Gaussian process. In other cases, the central limit theorem
indicates that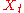
will be approximately normally distributed when 
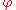is close to one.
The AR(p) model is given by the equation
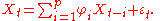
It is based on parameters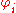
where i = 1, ..., p. There is a direct correspondence between these parameters and the covariance function of the process, and this correspondence can be inverted to determine the parameters from the autocorrelation function (which is itself obtained from the covariances). This is done using the Yule-Walker equations.
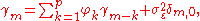
where m = 0, ... , p, yielding p + 1 equations.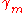
is the autocorrelation function of X, 
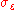is the standard deviation of the input noise process, and 
is the Kronecker delta function.
Because the last part of the equation is non-zero only if m = 0, the equation is usually solved by representing it as a matrix for m > 0, thus getting equation
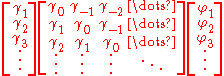
solving all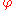
. For m = 0 we have
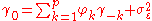
which allows us to solve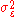
.
The above equations (the Yule-Walker equations) provide one route to estimating the parameters of an AR(p) model, by replacing the theoretical covariances with estimated values. One way of specifying the estimated covariances is equivalent to a calculation using least squares regression of values Xt on the p previous values of the same series.
Another usage is calculating the first p+1 elements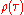
of the auto-correlation function. The full auto-correlation function can then be derived by recursively calculating
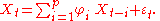
Multiplying both sides by Xt − m and taking expected value yields
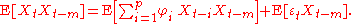
Now,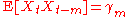
by definition of the autocorrelation function. The values of the noise function are independent of each other, and Xt − m is independent of εt where m is greater than zero. For m > 0, E[εtXt − m] = 0. For m = 0,
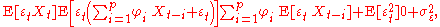
Now we have, for m ≥ 0,
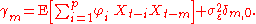
Furthermore,
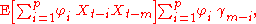
which yields the Yule-Walker equations:
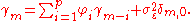
for m ≥ 0. For m < 0,
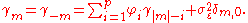
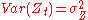is
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, an autoregressive (AR) model is a type of random process which is often used to model and predict various types of natural phenomena. The autoregressive model is one of a group of linear prediction
Linear prediction
Linear prediction is a mathematical operation where future values of a discrete-time signal are estimated as a linear function of previous samples....
formulas that attempt to predict an output of a system based on the previous outputs.
Definition
The notation AR(p) indicates an autoregressive model of order p. The AR(p) model is defined as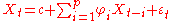where
are the parameters of the model, is a constant (often omitted for simplicity) and 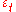is white noiseWhite noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
.
An autoregressive model can thus be viewed as the output of an all-pole infinite impulse response
Infinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
filter whose input is white noise.
Some constraints are necessary on the values of the parameters of this model in order that the model remains wide-sense stationary. For example, processes in the AR(1) model with |φ1| ≥ 1 are not stationary. More generally, for an AR(p) model to be wide-sense stationary, the roots of the polynomial
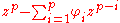must lie within the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, i.e., each root
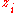must satisfy .Example: An AR(1)-process
An AR(1)-process is given by: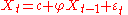where
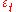is a white noise process with zero mean and variance 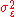.(Note: The subscript on
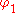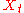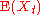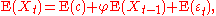
has been dropped.) The process is wide-sense stationary if since it is obtained as the output of a stable filter whose input is white noise. (If then has infinite variance, and is therefore not wide sense stationary.) Consequently, assuming , the mean is identical for all values of t. If the mean is denoted by , it follows fromthat
and hence
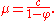
In particular, if
, then the mean is 0.The variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
is
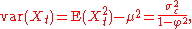
where
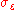is the standard deviation of 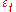. This can be shown by noting thatand then by noticing that the quantity above is a stable fixed point of this relation.
The autocovariance
Autocovariance
In statistics, given a real stochastic process X, the autocovariance is the covariance of the variable with itself, i.e. the variance of the variable against a time-shifted version of itself...
is given by
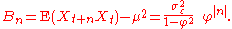
It can be seen that the autocovariance function decays with a decay time (also called time constant
Time constant
In physics and engineering, the time constant, usually denoted by the Greek letter \tau , is the risetime characterizing the response to a time-varying input of a first-order, linear time-invariant system.Concretely, a first-order LTI system is a system that can be modeled by a single first order...
) of
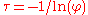[to see this, write 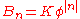where is independent of . Then note that 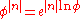and match this to the exponential decay law 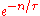].The spectral density
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
function is the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the autocovariance function. In discrete terms this will be the discrete-time Fourier transform:
This expression is periodic due to the discrete nature of the
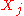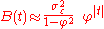
, which is manifested as the cosine term in the denominator. If we assume that the sampling time () is much smaller than the decay time (), then we can use a continuum approximation to :which yields a Lorentzian profile
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
for the spectral density:
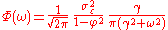
where
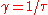is the angular frequency associated with the decay time .An alternative expression for
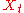can be derived by first substituting 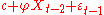for 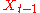in the defining equation. Continuing this process N times yields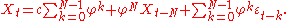For N approaching infinity,
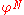will approach zero and: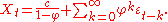It is seen that
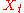is white noise convolved with the 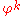kernel plus the constant mean. If the white noise 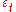is a Gaussian processGaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
then
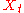is also a Gaussian process. In other cases, the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
indicates that
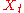will be approximately normally distributed when 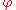is close to one.Calculation of the AR parameters
There are many ways to estimate the coefficients: the OLS procedure, method of moments (through Yule Walker equations),MCMC.The AR(p) model is given by the equation
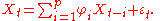
It is based on parameters
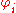where i = 1, ..., p. There is a direct correspondence between these parameters and the covariance function of the process, and this correspondence can be inverted to determine the parameters from the autocorrelation function (which is itself obtained from the covariances). This is done using the Yule-Walker equations.Yule-Walker equations
The Yule-Walker equations are the following set of equations.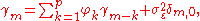where m = 0, ... , p, yielding p + 1 equations.
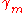is the autocorrelation function of X, 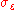is the standard deviation of the input noise process, and is the Kronecker delta function.Because the last part of the equation is non-zero only if m = 0, the equation is usually solved by representing it as a matrix for m > 0, thus getting equation
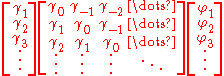
solving all
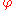. For m = 0 we have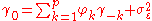which allows us to solve
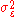.The above equations (the Yule-Walker equations) provide one route to estimating the parameters of an AR(p) model, by replacing the theoretical covariances with estimated values. One way of specifying the estimated covariances is equivalent to a calculation using least squares regression of values Xt on the p previous values of the same series.
Another usage is calculating the first p+1 elements
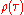of the auto-correlation function. The full auto-correlation function can then be derived by recursively calculating-
- Examples for some Low-order AR(p) processes
- p=1
-
- Hence
-
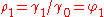
- p=2
- The Yule-Walker equations for an AR(2) process are
- Remember that
- Using the first equation yields
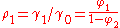
- Using the recursion formula yields
-
- The Yule-Walker equations for an AR(2) process are
- p=1
Derivation
The equation defining the AR process is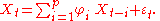Multiplying both sides by Xt − m and taking expected value yields
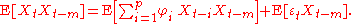
Now,
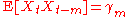by definition of the autocorrelation function. The values of the noise function are independent of each other, and Xt − m is independent of εt where m is greater than zero. For m > 0, E[εtXt − m] = 0. For m = 0,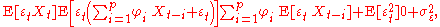Now we have, for m ≥ 0,
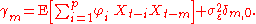
Furthermore,
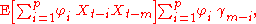
which yields the Yule-Walker equations:
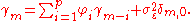
for m ≥ 0. For m < 0,
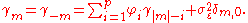
Spectrum
The power spectral density of an AR(p) process with noise variance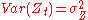 is
AR(1)
For AR(1)-
- If
there is a single spectral peak at f=0, often referred to as red noise. As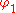 
becomes nearer 1, there is stronger power at low frequencies, i.e. larger time lags. - If
there is a minimum at f=0, often referred to as blue noise
AR(2)
AR(2) processes can be split into three groups depending on the characteristics of their roots:
- When
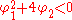, the process has a pair of complex-conjugate roots, creating a mid-frequency peak at:
Otherwise the process has real roots, and:- When
it acts as a low-pass filter on the white noise with a spectral peak at 
- When
it acts as a high-pass filter on the white noise with a spectral peak at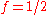 
.
The process is stable when the roots are within the unit circle, or equivalently when the coefficients are in the triangle
.
The full PSD function can be expressed in real form as: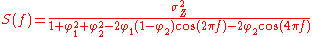
Characteristic polynomial
Auto-correlation functionAutocorrelationAutocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
of an AR(p) process can be expressed as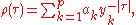
where
are the roots of the polynomial
Auto-correlation function of an AR(p) process is a sum of decaying exponential.- Each real root contributes a component to the auto-correlation function that decays exponentially.
- Similarly, each pair of complex conjugate roots contributes an exponentially damped oscillation.
Implementations in statistics packages
- RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
, the stats package includes an ar function.
See also
- Moving average modelMoving average modelIn time series analysis, the moving-average model is a common approach for modeling univariate time series models. The notation MA refers to the moving average model of order q:...
- Autoregressive moving average modelAutoregressive moving average modelIn statistics and signal processing, autoregressive–moving-average models, sometimes called Box–Jenkins models after the iterative Box–Jenkins methodology usually used to estimate them, are typically applied to autocorrelated time series data.Given a time series of data Xt, the ARMA model is a...
- Predictive analyticsPredictive analyticsPredictive analytics encompasses a variety of statistical techniques from modeling, machine learning, data mining and game theory that analyze current and historical facts to make predictions about future events....
- Linear predictive codingLinear predictive codingLinear predictive coding is a tool used mostly in audio signal processing and speech processing for representing the spectral envelope of a digital signal of speech in compressed form, using the information of a linear predictive model...
External links
- If
