Gaussian process
Encyclopedia
In probability theory
and statistics
, a Gaussian process is a stochastic process
whose realisations consist of random values
associated with every point in a range of times (or of space) such that each such random variable
has a normal distribution. Moreover, every finite collection of those random variables has a multivariate normal distribution.
Gaussian processes are important in statistical model
ling because of properties inherited from the normal. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quantities include: the average value of the process over a range of times; the error in estimating the average using sample values at a small set of times.
{ Xt ; t ∈ T } for which any finite linear combination
of samples
will be normally distributed (or, more generally, any linear functional
applied to the sample function Xt will give a normally distributed result).
Some authors also assume the random variable
s Xt have mean zero.
simply because the normal distribution
is sometimes called the Gaussian distribution, although Gauss was not the first to study that distribution: see history of the normal/Gaussian distribution.
for every finite set of indices
t1, ..., tk in the index set T
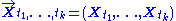
is a multivariate Gaussian random variable
. Using characteristic functions
of random variables, the Gaussian property can be formulated as follows:{ Xt ; t ∈ T } is Gaussian if and only if, for every finite set of indices t1, ..., tk, there are reals σl j with σi i > 0 and reals μj such that
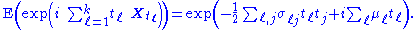
The numbers σl j and μj can be shown to be the covariance
s and means of the variables in the process.
is perhaps the most widely studied Gaussian process. It is not stationary
, but it has stationary increments.
The Ornstein–Uhlenbeck process is a stationary
Gaussian process.
The Brownian bridge
is a Gaussian process whose increments are not independent
.
The fractional Brownian motion is a Gaussian process whose covariance function is a generalisation of Wiener process.
in Bayesian inference
. (Given any set of
points in the desired domain of your functions, take a multivariate Gaussian whose covariance matrix
parameter is the Gram matrix of your N points with some desired kernel
, and sample from that Gaussian.) Inference of continuous values with a Gaussian process prior is known as Gaussian process regression, or Kriging
. Gaussian processes are also useful as a powerful non-linear interpolation
tool. Gaussian processes can also be used for probabilistic classification.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a Gaussian process is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
whose realisations consist of random values
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
associated with every point in a range of times (or of space) such that each such random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
has a normal distribution. Moreover, every finite collection of those random variables has a multivariate normal distribution.
Gaussian processes are important in statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
ling because of properties inherited from the normal. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quantities include: the average value of the process over a range of times; the error in estimating the average using sample values at a small set of times.
Definition
A Gaussian process is a stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
{ Xt ; t ∈ T } for which any finite linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of samples
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
will be normally distributed (or, more generally, any linear functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
applied to the sample function Xt will give a normally distributed result).
Some authors also assume the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s Xt have mean zero.
History
The concept is named after Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
simply because the normal distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
is sometimes called the Gaussian distribution, although Gauss was not the first to study that distribution: see history of the normal/Gaussian distribution.
Alternative definitions
Alternatively, a process is Gaussian if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for every finite set of indices
Index (mathematics)
The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
t1, ..., tk in the index set T
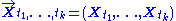
is a multivariate Gaussian random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
. Using characteristic functions
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of random variables, the Gaussian property can be formulated as follows:{ Xt ; t ∈ T } is Gaussian if and only if, for every finite set of indices t1, ..., tk, there are reals σl j with σi i > 0 and reals μj such that
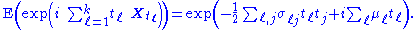
The numbers σl j and μj can be shown to be the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
s and means of the variables in the process.
Important Gaussian processes
The Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
is perhaps the most widely studied Gaussian process. It is not stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
, but it has stationary increments.
The Ornstein–Uhlenbeck process is a stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
Gaussian process.
The Brownian bridge
Brownian bridge
A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
is a Gaussian process whose increments are not independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
.
The fractional Brownian motion is a Gaussian process whose covariance function is a generalisation of Wiener process.
Applications
A Gaussian process can be used as a prior probability distribution over functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
in Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
. (Given any set of
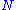points in the desired domain of your functions, take a multivariate Gaussian whose covariance matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
parameter is the Gram matrix of your N points with some desired kernel
Stochastic kernel
In statistics, a stochastic kernel estimate is an estimate of the transition function of a stochastic process. Often, this is an estimate of the conditional density function obtained using kernel density estimation...
, and sample from that Gaussian.) Inference of continuous values with a Gaussian process prior is known as Gaussian process regression, or Kriging
Kriging
Kriging is a group of geostatistical techniques to interpolate the value of a random field at an unobserved location from observations of its value at nearby locations....
. Gaussian processes are also useful as a powerful non-linear interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
tool. Gaussian processes can also be used for probabilistic classification.
External links
- www.GaussianProcess.com
- The Gaussian Processes Web Site, including the text of Rasmussen and Williams' Gaussian Processes for Machine Learning
- A gentle introduction to Gaussian processes
- A Review of Gaussian Random Fields and Correlation Functions