
Bayesian inference
Encyclopedia
In statistics, Bayesian inference is a method of statistical inference
. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection. Bayesian inference may be contrasted to frequentist inference
, which uses the sampling distribution of a statistic.
In the Bayesian interpretation of probability
, probability measures confidence that something is true, and may be termed confidence, uncertainty or belief. In practical usage, Bayesian inference is often viewed as an iterative process in which the confidence distribution on the value of a variable is updated as evidence for the value is observed. In each iteration, the initial distribution is called the prior
and the modified distribution the posterior
.
In more detail, suppose there is a real process, generating independent events with an unknown probability distribution. It is assumed that the distribution corresponds to some model, parametrised by the variable . The state of belief concerning this process is the set of possible models (one for each value of
. The state of belief concerning this process is the set of possible models (one for each value of  ) and corresponding confidences. The confidences are subjective, but always sum to 1. When events are freshly observed, they may be compared to those predicted by each model and the confidences updated. This is achieved mathematically using Bayes' theorem
) and corresponding confidences. The confidences are subjective, but always sum to 1. When events are freshly observed, they may be compared to those predicted by each model and the confidences updated. This is achieved mathematically using Bayes' theorem
. Typically, as iterations occur, the confidence in one model tends to 1 while that of the rest tend to 0.
In Bayesian model selection, the uncertainty of different models is compared as inference steps occur. For further details of the use of Bayesian inference in model selection, see Bayesian model selection.
 , but the probability distribution is unknown. Let the event space
, but the probability distribution is unknown. Let the event space  represent the current state of belief for this process. Each model is represented by
represent the current state of belief for this process. Each model is represented by  . The conditional probabilities
. The conditional probabilities  are specified to define the model.
are specified to define the model. 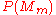 is the confidence of model
is the confidence of model  . Before the first inference step,
. Before the first inference step, 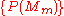 is a set of arbitrary initial prior probabilities.
is a set of arbitrary initial prior probabilities.
Suppose that the process is observed to generate event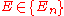 . For each model
. For each model  ,
,  is updated to
is updated to 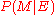 . From Bayes' theorem
. From Bayes' theorem
:

Upon observation of further evidence, this procedure may be repeated.
 be a set of independent identically distributed observations, where each
be a set of independent identically distributed observations, where each 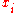 is distributed according to
is distributed according to 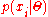 .
.  is an unknown vector of parameters and predictions to be inferred from the observations. Initially, confidence in
is an unknown vector of parameters and predictions to be inferred from the observations. Initially, confidence in  is distributed according to some prior distribution
is distributed according to some prior distribution  with the vector of hyperparameters
with the vector of hyperparameters
 .
.
From the conditional independence
of the observations, the joint probability density of given
given  is
is

As the observations are conditionally independent of ,
,


Bayes' theorem
is then applied to determine the posterior distribution :
:

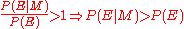 . That is, if the model were true, the evidence would be more likely than is predicted by the current state of belief. The reverse applies for a decrease in confidence. If the confidence does not change,
. That is, if the model were true, the evidence would be more likely than is predicted by the current state of belief. The reverse applies for a decrease in confidence. If the confidence does not change, 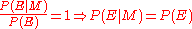 . That is, the evidence is independent of the model. If the model were true, the evidence would be exactly as likely as predicted by the current state of belief.
. That is, the evidence is independent of the model. If the model were true, the evidence would be exactly as likely as predicted by the current state of belief.
 then
then 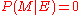 . Similarly, if
. Similarly, if 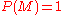 , then
, then  .
.
The former can be proved by inspection of Bayes' theorem. The latter can be proved by considering that . Therefore,
. Therefore, 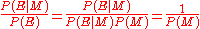 . The result now follows by substitution into Bayes' theorem.
. The result now follows by substitution into Bayes' theorem.
Cromwell's rule can be interpreted to mean that hard convictions are insensitive to counter-evidence.
gives that in the limit of infinite trials and the posterior converges to a Gaussian distribution independent of the initial prior under some conditions firstly outlined and rigorously proven by Joseph Leo Doob
in 1948, namely if the random variable in consideration has a finite probability space
. The more general results were obtained later by the statistician David A. Freedman
who published in two seminal research papers in 1963 and 1965 when and under what circumstances the asymptotic behaviour of posterior is guaranteed. His 1963 paper treats like Doob (1949) the finite case and comes to a satisfactory conclusion. However, if the random variable has an infinite but countable probability space
(i.e. corresponding to a die with infinite many faces) the 1965 paper demonstrates that for a dense subset of priors the Bernstein-von Mises theorem
is not applicable. In this case there is almost surely
no asymptotic convergence. Similar results were obtained in 1964 by Lorraine Schwarz. Later in the eighties and nineties Freedman
and Persi Diaconis
continued to work on the case of infinite countable probability spaces.
We conclude that in practise, there may be insufficient trials to suppress the effects of the initial choice, and especially for large (but finite) systems the convergence might be very slow.
. For each family of distributions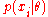 , there will be an associated conjugate prior
, there will be an associated conjugate prior
family. The usefulness of the conjugate prior is that if the prior distribution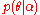 is chosen from this family, the posterior distribution of a single observation, or of a set of independent identically distributed observations, will be in the same family, and the integral in the denominator of the above calculation will be tractable
is chosen from this family, the posterior distribution of a single observation, or of a set of independent identically distributed observations, will be in the same family, and the integral in the denominator of the above calculation will be tractable
.
, the mean
, the variance
, the median, etc.). If a point estimate of the parameter is desired, a maximum a posteriori
estimate can be computed, i.e.:
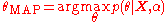
This could then be used to make predictions about new observations.
However, the "properly" Bayesian tendency is to work with the entire distribution, and make predictions by marginalizing
over the distribution. For example, the predictive density of a new observation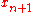 can be determined by
can be determined by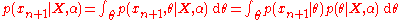
Furthermore, when making a point estimate of a parameter, Bayesians generally prefer to use the mean
rather than the mode
, i.e.
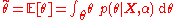
Intuitively, it seems clear that the answer should be more than a half, since there are more plain cookies in bowl #1. The precise answer is given by Bayes' theorem. Let correspond to bowl #1, and
correspond to bowl #1, and  to bowl #2.
to bowl #2.
It is given that the bowls are identical from Fred's point of view, thus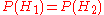 , and the two must add up to 1, so both are equal to 0.5.
, and the two must add up to 1, so both are equal to 0.5.
The event is the observation of a plain cookie. From the contents of the bowls, we know that
is the observation of a plain cookie. From the contents of the bowls, we know that  and
and  . Bayes' formula then yields
. Bayes' formula then yields
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection. Bayesian inference may be contrasted to frequentist inference
Frequentist inference
Frequentist inference is one of a number of possible ways of formulating generally applicable schemes for making statistical inferences: that is, for drawing conclusions from statistical samples. An alternative name is frequentist statistics...
, which uses the sampling distribution of a statistic.
In the Bayesian interpretation of probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
, probability measures confidence that something is true, and may be termed confidence, uncertainty or belief. In practical usage, Bayesian inference is often viewed as an iterative process in which the confidence distribution on the value of a variable is updated as evidence for the value is observed. In each iteration, the initial distribution is called the prior
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
and the modified distribution the posterior
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
.
In more detail, suppose there is a real process, generating independent events with an unknown probability distribution. It is assumed that the distribution corresponds to some model, parametrised by the variable
 . The state of belief concerning this process is the set of possible models (one for each value of
. The state of belief concerning this process is the set of possible models (one for each value of  ) and corresponding confidences. The confidences are subjective, but always sum to 1. When events are freshly observed, they may be compared to those predicted by each model and the confidences updated. This is achieved mathematically using Bayes' theorem
) and corresponding confidences. The confidences are subjective, but always sum to 1. When events are freshly observed, they may be compared to those predicted by each model and the confidences updated. This is achieved mathematically using Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
. Typically, as iterations occur, the confidence in one model tends to 1 while that of the rest tend to 0.
In Bayesian model selection, the uncertainty of different models is compared as inference steps occur. For further details of the use of Bayesian inference in model selection, see Bayesian model selection.
General view
Suppose a process is generating independent and identically distributed events , but the probability distribution is unknown. Let the event space
, but the probability distribution is unknown. Let the event space  represent the current state of belief for this process. Each model is represented by
represent the current state of belief for this process. Each model is represented by  . The conditional probabilities
. The conditional probabilities  are specified to define the model.
are specified to define the model. 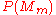 is the confidence of model
is the confidence of model  . Before the first inference step,
. Before the first inference step, 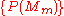 is a set of arbitrary initial prior probabilities.
is a set of arbitrary initial prior probabilities.Suppose that the process is observed to generate event
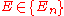 . For each model
. For each model  ,
,  is updated to
is updated to 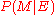 . From Bayes' theorem
. From Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
:

-
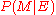 , the posteriorPosterior probabilityIn Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
, the posteriorPosterior probabilityIn Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
, is the confidence in after
after  is observed.
is observed. -
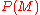 , the priorPrior probabilityIn Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
, the priorPrior probabilityIn Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
, is the confidence in before
before  is observed.
is observed. -
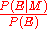 is a factor representing the impact of
is a factor representing the impact of  on the confidence in
on the confidence in  . The numerator is called the likelihoodLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
. The numerator is called the likelihoodLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
.
Upon observation of further evidence, this procedure may be repeated.
Parametric view
Let be a set of independent identically distributed observations, where each
be a set of independent identically distributed observations, where each 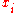 is distributed according to
is distributed according to 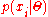 .
.  is an unknown vector of parameters and predictions to be inferred from the observations. Initially, confidence in
is an unknown vector of parameters and predictions to be inferred from the observations. Initially, confidence in  is distributed according to some prior distribution
is distributed according to some prior distribution  with the vector of hyperparameters
with the vector of hyperparametersHyperparameter
In Bayesian statistics, a hyperparameter is a parameter of a prior distribution; the term is used to distinguish them from parameters of the model for the underlying system under analysis...
 .
.From the conditional independence
Conditional independence
In probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
of the observations, the joint probability density of
 given
given  is
is
As the observations are conditionally independent of
 ,
,

Bayes' theorem
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
is then applied to determine the posterior distribution
 :
:
Interpretation of factor
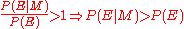 . That is, if the model were true, the evidence would be more likely than is predicted by the current state of belief. The reverse applies for a decrease in confidence. If the confidence does not change,
. That is, if the model were true, the evidence would be more likely than is predicted by the current state of belief. The reverse applies for a decrease in confidence. If the confidence does not change, 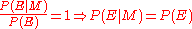 . That is, the evidence is independent of the model. If the model were true, the evidence would be exactly as likely as predicted by the current state of belief.
. That is, the evidence is independent of the model. If the model were true, the evidence would be exactly as likely as predicted by the current state of belief.Cromwell's rule
If then
then 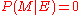 . Similarly, if
. Similarly, if 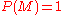 , then
, then  .
.The former can be proved by inspection of Bayes' theorem. The latter can be proved by considering that
 . Therefore,
. Therefore, 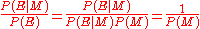 . The result now follows by substitution into Bayes' theorem.
. The result now follows by substitution into Bayes' theorem.Cromwell's rule can be interpreted to mean that hard convictions are insensitive to counter-evidence.
Asymptotic behaviour of posterior
Consider the behaviour of a belief distribution as it is updated a large number of times with independent and identically distributed trials. For sufficiently nice prior probabilities, the Bernstein-von Mises theoremBernstein–von Mises theorem
In Bayesian inference, the Bernstein–von Mises theorem provides the basis for the important result that the posterior distribution for unknown quantities in any problem is effectively independent of the prior distribution once the amount of information supplied by a sample of data is large...
gives that in the limit of infinite trials and the posterior converges to a Gaussian distribution independent of the initial prior under some conditions firstly outlined and rigorously proven by Joseph Leo Doob
Joseph Leo Doob
Joseph Leo Doob was an American mathematician, specializing in analysis and probability theory.The theory of martingales was developed by Doob.-Early life and education:...
in 1948, namely if the random variable in consideration has a finite probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
. The more general results were obtained later by the statistician David A. Freedman
David A. Freedman (statistician)
David A. Freedman was Professor of Statistics at the University of California, Berkeley. He was a distinguished mathematical statistician whose wide-ranging research included the analysis of martingale inequalities, Markov processes, de Finetti's theorem, consistency of Bayes estimators, sampling,...
who published in two seminal research papers in 1963 and 1965 when and under what circumstances the asymptotic behaviour of posterior is guaranteed. His 1963 paper treats like Doob (1949) the finite case and comes to a satisfactory conclusion. However, if the random variable has an infinite but countable probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(i.e. corresponding to a die with infinite many faces) the 1965 paper demonstrates that for a dense subset of priors the Bernstein-von Mises theorem
Bernstein–von Mises theorem
In Bayesian inference, the Bernstein–von Mises theorem provides the basis for the important result that the posterior distribution for unknown quantities in any problem is effectively independent of the prior distribution once the amount of information supplied by a sample of data is large...
is not applicable. In this case there is almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
no asymptotic convergence. Similar results were obtained in 1964 by Lorraine Schwarz. Later in the eighties and nineties Freedman
David A. Freedman (statistician)
David A. Freedman was Professor of Statistics at the University of California, Berkeley. He was a distinguished mathematical statistician whose wide-ranging research included the analysis of martingale inequalities, Markov processes, de Finetti's theorem, consistency of Bayes estimators, sampling,...
and Persi Diaconis
Persi Diaconis
Persi Warren Diaconis is an American mathematician and former professional magician. He is the Mary V. Sunseri Professor of Statistics and Mathematics at Stanford University....
continued to work on the case of infinite countable probability spaces.
We conclude that in practise, there may be insufficient trials to suppress the effects of the initial choice, and especially for large (but finite) systems the convergence might be very slow.
Conjugate priors
For mathematical convenience, the prior distribution is often assumed to come from a particular family of distributions called a conjugate priorConjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
. For each family of distributions
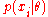 , there will be an associated conjugate prior
, there will be an associated conjugate priorConjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
family. The usefulness of the conjugate prior is that if the prior distribution
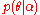 is chosen from this family, the posterior distribution of a single observation, or of a set of independent identically distributed observations, will be in the same family, and the integral in the denominator of the above calculation will be tractable
is chosen from this family, the posterior distribution of a single observation, or of a set of independent identically distributed observations, will be in the same family, and the integral in the denominator of the above calculation will be tractableTractable
Tractable may refer to:*Operation Tractable, a military operation in Normandy 1944*Tractability concerning how easily something can be done...
.
Estimates of parameters and predictions
Once the posterior distribution of the parameter is determined, any desired statistic regarding the distribution can be determined (e.g. the most likely value or modeMode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
, the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, the median, etc.). If a point estimate of the parameter is desired, a maximum a posteriori
Maximum a posteriori
In Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
estimate can be computed, i.e.:
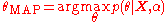
This could then be used to make predictions about new observations.
However, the "properly" Bayesian tendency is to work with the entire distribution, and make predictions by marginalizing
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
over the distribution. For example, the predictive density of a new observation
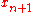 can be determined by
can be determined by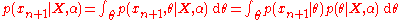
Furthermore, when making a point estimate of a parameter, Bayesians generally prefer to use the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
rather than the mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
, i.e.
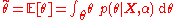
Testing a hypothesis
Suppose there are two full bowls of cookies. Bowl #1 has 10 chocolate chip and 30 plain cookies, while bowl #2 has 20 of each. Our friend Fred picks a bowl at random, and then picks a cookie at random. We may assume there is no reason to believe Fred treats one bowl differently from another, likewise for the cookies. The cookie turns out to be a plain one. How probable is it that Fred picked it out of bowl #1?Intuitively, it seems clear that the answer should be more than a half, since there are more plain cookies in bowl #1. The precise answer is given by Bayes' theorem. Let
 correspond to bowl #1, and
correspond to bowl #1, and  to bowl #2.
to bowl #2.It is given that the bowls are identical from Fred's point of view, thus
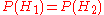 , and the two must add up to 1, so both are equal to 0.5.
, and the two must add up to 1, so both are equal to 0.5.The event
 is the observation of a plain cookie. From the contents of the bowls, we know that
is the observation of a plain cookie. From the contents of the bowls, we know that  and
and  . Bayes' formula then yields
. Bayes' formula then yields-

Before we observed the cookie, the probability we assigned for Fred having chosen bowl #1 was the prior probability, , which was 0.5. After observing the cookie, we must revise the probability to
, which was 0.5. After observing the cookie, we must revise the probability to 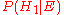 , which is 0.6.
, which is 0.6.
Making a prediction
An archaeologist is working at a site thought to be from the medieval period, between the 11th century to the 16th century. However, it is uncertain exactly when in this period the site was inhabited. Fragments of pottery are found, some of which are glazed and some of which are decorated. It is expected that if the site were inhabited during the early medieval period, then 1% of the pottery would be glazed and 50% of its area decorated, whereas if it had been inhabited in the late medieval period then 81% would be glazed and 5% of its area decorated. How confident can the archaeologist be in estimating the period of inhabitation as fragments are unearthed?
The confidence in the continuous variable (century) is to be calculated, with the discrete set of events
(century) is to be calculated, with the discrete set of events 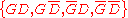 as evidence. Assuming linear variation of glaze and decoration with time, and that these variables are independent,
as evidence. Assuming linear variation of glaze and decoration with time, and that these variables are independent,
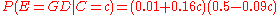
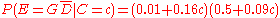


Assume a uniform prior of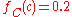 , and that trials are independent and identically distributed. When a new fragment of type
, and that trials are independent and identically distributed. When a new fragment of type  is discovered, Bayes' theorem is applied to update the confidence for each
is discovered, Bayes' theorem is applied to update the confidence for each  :
:

A computer simulation of the changing confidence as 50 fragments are unearthed is shown on the graph. In the simulation, the site was inhabited around 1420, or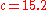 . By calculating the area under the relevant portion of the graph for 50 trials, the archaeologist can say that there is practically no chance the site was inhabited in the 11th and 12th centuries, about 1% chance that it was inhabited during the 13th century, 63% chance during the 14th century and 36% during the 15th century.Note that the Bernstein-von Mises theoremBernstein–von Mises theoremIn Bayesian inference, the Bernstein–von Mises theorem provides the basis for the important result that the posterior distribution for unknown quantities in any problem is effectively independent of the prior distribution once the amount of information supplied by a sample of data is large...
. By calculating the area under the relevant portion of the graph for 50 trials, the archaeologist can say that there is practically no chance the site was inhabited in the 11th and 12th centuries, about 1% chance that it was inhabited during the 13th century, 63% chance during the 14th century and 36% during the 15th century.Note that the Bernstein-von Mises theoremBernstein–von Mises theoremIn Bayesian inference, the Bernstein–von Mises theorem provides the basis for the important result that the posterior distribution for unknown quantities in any problem is effectively independent of the prior distribution once the amount of information supplied by a sample of data is large...
asserts here the asymptotic convergence to the "true" distribution because the probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
corresponding to the discrete set of events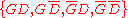 is finite (see above section on asymptotic behaviour of the posterior).
is finite (see above section on asymptotic behaviour of the posterior).
Computer applications
Bayesian inference has applications in artificial intelligenceArtificial intelligenceArtificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
and expert systemExpert systemIn artificial intelligence, an expert system is a computer system that emulates the decision-making ability of a human expert. Expert systems are designed to solve complex problems by reasoning about knowledge, like an expert, and not by following the procedure of a developer as is the case in...
s. Bayesian inference techniques have been a fundamental part of computerized pattern recognitionPattern recognitionIn machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
techniques since the late 1950s. There is also an ever growing connection between Bayesian methods and simulation-based Monte CarloMonte Carlo methodMonte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
techniques since complex models cannot be processed in closed form by a Bayesian analysis, while a graphical modelGraphical modelA graphical model is a probabilistic model for which a graph denotes the conditional independence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning....
structure may allow for efficient simulation algorithms like the Gibbs samplingGibbs samplingIn statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is an algorithm to generate a sequence of samples from the joint probability distribution of two or more random variables...
and other Metropolis–Hastings algorithm schemes. Recently Bayesian inference has gained popularity amongst the phylogeneticsPhylogeneticsIn biology, phylogenetics is the study of evolutionary relatedness among groups of organisms , which is discovered through molecular sequencing data and morphological data matrices...
community for these reasons; a number of applications allow many demographic and evolutionary parameters to be estimated simultaneously. In the areas of population geneticsPopulation geneticsPopulation genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
and dynamical systems theoryDynamical systems theoryDynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
approximate Bayesian computationApproximate Bayesian computationApproximate Bayesian computation is a family of computational techniques in Bayesian statistics. These simulation techniques operate on summary data to make broad inferences with less computation than might be required if all available data were analyzed in detail...
(ABC) are also becoming increasingly popular.
As applied to statistical classification, Bayesian inference has been used in recent years to develop algorithms for identifying e-mail spamE-mail spamEmail spam, also known as junk email or unsolicited bulk email , is a subset of spam that involves nearly identical messages sent to numerous recipients by email. Definitions of spam usually include the aspects that email is unsolicited and sent in bulk. One subset of UBE is UCE...
. Applications which make use of Bayesian inference for spam filtering include DSPAMDSPAMDSPAM is a free software statistical spam filter written by Jonathan A. Zdziarski, author of the book Ending Spam and other books. It is intended to be a scalable, content-based spam filter for large multi-user systems...
, BogofilterBogofilterBogofilter is a mail filter that classifies e-mail as spam or ham by a statistical analysis of the message's header and content . The program is able to learn from the user's classifications and corrections. It was originally written by Eric S...
, SpamAssassinSpamAssassinSpamAssassin is a computer program released under the Apache License 2.0 used for e-mail spam filtering based on content-matching rules. It is now part of the Apache Foundation....
, SpamBayesSpamBayesSpamBayes is a Bayesian spam filter written in Python which uses techniques laid out by Paul Graham in his essay "A Plan for Spam". It has subsequently been improved by Gary Robinson and Tim Peters, among others....
, and MozillaMozillaMozilla is a term used in a number of ways in relation to the Mozilla.org project and the Mozilla Foundation, their defunct commercial predecessor Netscape Communications Corporation, and their related application software....
. Spam classification is treated in more detail in the article on the naive Bayes classifierNaive Bayes classifierA naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong independence assumptions...
.
In the courtroom
Bayesian inference can be used by jurors to coherently accumulate the evidence for and against a defendant, and to see whether, in totality, it meets their personal threshold for 'beyond a reasonable doubtBeyond a Reasonable DoubtBeyond a Reasonable Doubt is a 1956 film directed by Fritz Lang and written by Douglas Morrow. The film, considered film noir, was the last American film directed by Lang.-Plot:...
'. The benefit of a Bayesian approach is that it gives the juror an unbiased, rational mechanism for combining evidence. Bayes' theorem is applied successively to all evidence presented, with the posterior from one stage becoming the prior for the next. A prior probability of guilt is still required. It has been suggested that this could reasonably be the probability that a random person taken from the qualifying population is guilty. Thus, for a crime known to have been committed by an adult male living in a town containing 50,000 adult males, the appropriate initial prior might be 1/50,000.
It may be appropriate to explain Bayes' theorem to jurors in odds form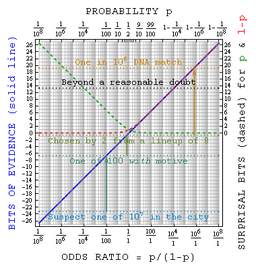 Bayes' ruleIn probability theory and applications, Bayes' rule relates the odds of event A_1 to event A_2, before and after conditioning on event B. The relationship is expressed in terms of the Bayes factor, \Lambda. Bayes' rule is derived from and closely related to Bayes' theorem...
Bayes' ruleIn probability theory and applications, Bayes' rule relates the odds of event A_1 to event A_2, before and after conditioning on event B. The relationship is expressed in terms of the Bayes factor, \Lambda. Bayes' rule is derived from and closely related to Bayes' theorem...
, as betting odds are more widely understood than probabilities. Alternatively, a logarithmic approachGambling and information theoryStatistical inference might be thought of as gambling theory applied to the world around. The myriad applications for logarithmic information measures tell us precisely how to take the best guess in the face of partial information. In that sense, information theory might be considered a formal...
, replacing multiplication with addition, might be easier for a jury to handle.
The use of Bayes' theorem by jurors is controversial. In the United Kingdom, a defence expert witnessExpert witnessAn expert witness, professional witness or judicial expert is a witness, who by virtue of education, training, skill, or experience, is believed to have expertise and specialised knowledge in a particular subject beyond that of the average person, sufficient that others may officially and legally...
explained Bayes' theorem to the jury in R v Adams. The jury convicted, but the case went to appeal on the basis that no means of accumulating evidence had been provided for jurors who did not wish to use Bayes' theorem. The Court of Appeal upheld the conviction, but it also gave the opinion that "To introduce Bayes' Theorem, or any similar method, into a criminal trial plunges the jury into inappropriate and unnecessary realms of theory and complexity, deflecting them from their proper task."
Gardner-Medwin argues that the criterion on which a verdict in a criminal trial should be based is not the probability of guilt, but rather the probability of the evidence, given that the defendant is innocent (akin to a frequentist p-valueP-valueIn statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
). He argues that if the posterior probability of guilt is to be computed by Bayes' theorem, the prior probability of guilt must be known. This will depend on the incidence of the crime, which is an unusual piece of evidence to consider in a criminal trial. Consider the following three propositions:
- A The known facts and testimony could have arisen if the defendant is guilty
- B The known facts and testimony could have arisen if the defendant is innocent
- C The defendant is guilty.
Gardner-Medwin argues that the jury should believe both A and not-B in order to convict. A and not-B implies the truth of C, but the reverse is not true. It is possible that B and C are both true, but in this case he argues that a jury should acquit, even though they know that they will be letting some guilty people go free. See also Lindley's paradoxLindley's paradoxLindley's paradox is a counterintuitive situation in statistics in which the Bayesian and frequentist approaches to a hypothesis testing problem give opposite results for certain choices of the prior distribution...
.
Other
- The scientific methodScientific methodScientific method refers to a body of techniques for investigating phenomena, acquiring new knowledge, or correcting and integrating previous knowledge. To be termed scientific, a method of inquiry must be based on gathering empirical and measurable evidence subject to specific principles of...
is sometimes interpreted as an application of Bayesian inference. In this view, Bayes' rule guides (or should guide) the updating of probabilities about hypothesesHypothesisA hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
conditional on new observations or experimentExperimentAn experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
s. - In March 2011, English HeritageEnglish HeritageEnglish Heritage . is an executive non-departmental public body of the British Government sponsored by the Department for Culture, Media and Sport...
reported the successful outcome of a research project by archaeologists at Cardiff UniversityCardiff UniversityCardiff University is a leading research university located in the Cathays Park area of Cardiff, Wales, United Kingdom. It received its Royal charter in 1883 and is a member of the Russell Group of Universities. The university is consistently recognised as providing high quality research-based...
, which demonstrated the possibility of using Bayesian inference to more accurately date prehistoric remains. - Bayesian search theoryBayesian search theoryBayesian search theory is the application of Bayesian statistics to the search for lost objects. It has been used several times to find lost sea vessels, for example the USS Scorpion.-Procedure:The usual procedure is as follows:...
is used to search for lost objects. - Bayesian inference in phylogenyBayesian inference in phylogenyBayesian inference in phylogeny generates a posterior distribution for a parameter, composed of a phylogenetic tree and a model of evolution, based on the prior for that parameter and the likelihood of the data, generated by a multiple alignment. The Bayesian approach has become more popular due...
- Bayesian tool for methylation analysisBayesian tool for methylation analysisBayesian tool for methylation analysis, also known as BATMAN, is a statistical tool for analyzing methylated DNA immunoprecipitation profiles...
Relation to decision theory
A decision-theoretic justification of the use of Bayesian inference was given by Abraham WaldAbraham Wald- See also :* Sequential probability ratio test * Wald distribution* Wald–Wolfowitz runs test...
, who proved that every Bayesian procedure is admissibleAdmissible decision ruleIn statistical decision theory, an admissible decision rule is a rule for making a decision such that there isn't any other rule that is always "better" than it, in a specific sense defined below....
.
Conversely, every admissibleAdmissible decision ruleIn statistical decision theory, an admissible decision rule is a rule for making a decision such that there isn't any other rule that is always "better" than it, in a specific sense defined below....
statistical procedure is either a Bayesian procedure or a limit of Bayesian procedures.
Wald's result also established the Bayesian approach as a fundamental technique in such areas of frequentist inferenceFrequentist inferenceFrequentist inference is one of a number of possible ways of formulating generally applicable schemes for making statistical inferences: that is, for drawing conclusions from statistical samples. An alternative name is frequentist statistics...
as point estimationPoint estimationIn statistics, point estimation involves the use of sample data to calculate a single value which is to serve as a "best guess" or "best estimate" of an unknown population parameter....
, hypothesis testing, and confidence intervals. Wald characterized admissible procedures as Bayesian procedures (and limits of Bayesian procedures), making the Bayesian formalism a central technique in such areas of frequentist statistics as parameter estimation, hypothesis testing, and computing confidence intervals. For example:- "Under some conditions, all admissible procedures are either Bayes procedures or limits of Bayes procedures (in various senses). These remarkable results, at least in their original form, are due essentially to Wald. They are useful because the property of being Bayes is easier to analyze than admissibility."
- "In decision theory, a quite general method for proving admissibility consists in exhibiting a procedure as a unique Bayes solution."
- "In the first chapters of this work, prior distributions with finite support and the corresponding Bayes procedures were used to establish some of the main theorems relating to the comparison of experiments. Bayes procedures with respect to more general prior distributions have played a very important in the development of statistics, including its asymptotic theory." "There are many problems where a glance at posterior distributions, for suitable priors, yields immediately interesting information. Also, this technique can hardly be avoided in sequential analysis."
- "A useful fact is that any Bayes decision rule obtained by taking a proper prior over the whole parameter space must be admissible"
- "An important area of investigation in the development of admissibility ideas has been that of conventional sampling-theory procedures, and many interesting results have been obtained."
Distribution of a parameter of the hypergeometric distribution
Consider a sample of marbleMarble (toy)A marble is a small spherical toy usually made from glass, clay, steel, or agate. These balls vary in size. Most commonly, they are about ½ inch in diameter, but they may range from less than ¼ inch to over 3 inches , while some art glass marbles fordisplay purposes are over 12 inches ...
marbleMarble (toy)A marble is a small spherical toy usually made from glass, clay, steel, or agate. These balls vary in size. Most commonly, they are about ½ inch in diameter, but they may range from less than ¼ inch to over 3 inches , while some art glass marbles fordisplay purposes are over 12 inches ...
s drawn from an urnUrn problemIn probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest are represented as colored balls in an urn or other container....
containing marbles.
marbles.
If the number of white marbles in the urn is known to be equal to , then the probability that the number of white marbles in the sample is equal to
, then the probability that the number of white marbles in the sample is equal to  , is
, is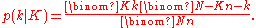 .
.
The mean number of white marbles in the sample is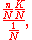
and the standard deviation is
An interesting situation is when the number of white marbles in the sample is known, and the number of white marbles in the urn is unknown.
If the number of white marbles in the sample is equal to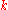 , then the degree of confidence that the number of white marbles in the urn is equal to
, then the degree of confidence that the number of white marbles in the urn is equal to  , is
, is
where is the probability that the number of white marbles in the urn is equal to
is the probability that the number of white marbles in the urn is equal to  , that is before observing the number of white marbles in the sample, and
, that is before observing the number of white marbles in the sample, and  is the probability that the number of white marbles in the sample is equal to
is the probability that the number of white marbles in the sample is equal to  , without knowing the number of white marbles in the urn.
, without knowing the number of white marbles in the urn.
Assume now that all the possibilities are considered equally likely in advance,
for
Then the degree of confidence that the number of white marbles in the urn is equal to , is
, is
The mean number of white marbles in the urn is
and the standard deviation is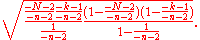
These two formulas regarding the number of white marbles in the urn emerge from the simpler formulas regarding the number of white marbles in the sample by the substitution
The limiting cases for ,
,  are the binomial distribution and the beta distribution, see below.
are the binomial distribution and the beta distribution, see below.
Posterior distribution of the binomial parameter
The problem considered by Bayes in Proposition 9 of his essay is the posterior distribution for the parameter of the binomial distribution.
Consider Bernoulli trialBernoulli trialIn the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
Bernoulli trialBernoulli trialIn the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s.
If the success probability is equal to , then the conditional probability of observing
, then the conditional probability of observing  successes is the (discrete) binomial distribution function
successes is the (discrete) binomial distribution function 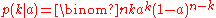 . The mean value of
. The mean value of 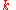 is
is  , and the standard deviation is
, and the standard deviation is  . The mean value of
. The mean value of  is
is  , and the standard deviation is
, and the standard deviation is  .
.
In the more realistic situation when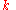 is known and
is known and  is unknown,
is unknown, 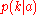 is a likelihood functionLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
is a likelihood functionLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
of . The posterior probabilityPosterior probabilityIn Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
. The posterior probabilityPosterior probabilityIn Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
distribution function of , after observing
, after observing 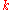 , is
, is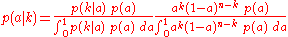
where a prior probabilityPrior probabilityIn Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
distribution function,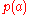 , is available to express what was known about
, is available to express what was known about  before observing
before observing 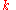 .
.
Assume now that the prior distribution is the continuous uniform distribution, for
for  .
.
Then the posterior distribution is the beta distribution,
is the beta distribution, 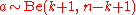 . The mean value of
. The mean value of  is
is 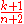 , rather than
, rather than  , and the standard deviation is
, and the standard deviation is 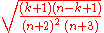 , rather than
, rather than  .
.
If the prior distribution is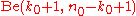 , then the posterior distribution is
, then the posterior distribution is  . So the beta distribution is a conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
. So the beta distribution is a conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
.
What is "Bayesian" about Proposition 9 is that Bayes presented it as a probability for the parameter . That is, not only can one compute probabilities for experimental outcomes, but also for the parameter which governs them, and the same algebra is used to make inferences of either kind. Interestingly, Bayes actually states his question in a way that might make the idea of assigning a probability distribution to a parameter palatable to a frequentist. He supposes that a billiard ball is thrown at random onto a billiard table, and that the probabilities p and q are the probabilities that subsequent billiard balls will fall above or below the first ball. By making the binomial parameter
. That is, not only can one compute probabilities for experimental outcomes, but also for the parameter which governs them, and the same algebra is used to make inferences of either kind. Interestingly, Bayes actually states his question in a way that might make the idea of assigning a probability distribution to a parameter palatable to a frequentist. He supposes that a billiard ball is thrown at random onto a billiard table, and that the probabilities p and q are the probabilities that subsequent billiard balls will fall above or below the first ball. By making the binomial parameter  depend on a random event, he cleverly escapes a philosophical quagmire that was an issue he most likely was not even aware of.
depend on a random event, he cleverly escapes a philosophical quagmire that was an issue he most likely was not even aware of.
History
The term Bayesian refers to Thomas BayesThomas BayesThomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...
(1702–1761), who proved a special case of what is now called Bayes' theoremBayes' theoremIn probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
. However, it was Pierre-Simon LaplacePierre-Simon LaplacePierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
(1749–1827) who introduced a general version of the theorem and used it to approach problems in celestial mechanicsCelestial mechanicsCelestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, medical statistics, reliabilityReliability (statistics)In statistics, reliability is the consistency of a set of measurements or of a measuring instrument, often used to describe a test. Reliability is inversely related to random error.-Types:There are several general classes of reliability estimates:...
, and jurisprudenceJurisprudenceJurisprudence is the theory and philosophy of law. Scholars of jurisprudence, or legal theorists , hope to obtain a deeper understanding of the nature of law, of legal reasoning, legal systems and of legal institutions...
. Early Bayesian inference, which used uniform priors following Laplace's principle of insufficient reason, was called "inverse probabilityInverse probabilityIn probability theory, inverse probability is an obsolete term for the probability distribution of an unobserved variable.Today, the problem of determining an unobserved variable is called inferential statistics, the method of inverse probability is called Bayesian probability, the "distribution"...
" (because it inferInductive reasoningInductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
s backwards from observations to parameters, or from effects to causes). After the 1920s, "inverse probability" was largely supplanted by a collection of methods that came to be called frequentist statistics.
In the 20th century, the ideas of Laplace were further developed in two different directions, giving rise to objective and subjective currents in Bayesian practice. In the objectivist stream, the statistical analysis depends on only the model assumed and the data analysed. No subjective decisions need to be involved. In contrast, "subjectivist" statisticians deny the possibility of fully objective analysis for the general case.
In the 1980s, there was a dramatic growth in research and applications of Bayesian methods, mostly attributed to the discovery of Markov chain Monte CarloMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
methods, which removed many of the computational problems, and an increasing interest in nonstandard, complex applications. Despite growth of Bayesian research, most undergraduate teaching is still based on frequentist statistics. Nonetheless, Bayesian methods are widely accepted and used, such as for example in the field of machine learningMachine learningMachine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
.
See also
- Approximate Bayesian computationApproximate Bayesian computationApproximate Bayesian computation is a family of computational techniques in Bayesian statistics. These simulation techniques operate on summary data to make broad inferences with less computation than might be required if all available data were analyzed in detail...
- Bayesian inference in phylogenyBayesian inference in phylogenyBayesian inference in phylogeny generates a posterior distribution for a parameter, composed of a phylogenetic tree and a model of evolution, based on the prior for that parameter and the likelihood of the data, generated by a multiple alignment. The Bayesian approach has become more popular due...
- Bayesian model comparison
- Bayesian brainBayesian brainBayesian brain is a term that is used to refer to the ability of the nervous system to operate in situations of uncertainty in a fashion that is close to the optimal prescribed by Bayesian statistics. This term is used in behavioural sciences and neuroscience and studies associated with this term...
- Bayesian estimation
- Bayesian filteringBayesian filteringBayesian filtering may refer to:* Bayesian spam filtering, a method to detect spam.* Recursive Bayesian estimation, a method to estimate the state of a system evolving in time.* Bayes' theorem...
- Bayesian networkBayesian networkA Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
- Bayesian probabilityBayesian probabilityBayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
- Bayesian tool for methylation analysisBayesian tool for methylation analysisBayesian tool for methylation analysis, also known as BATMAN, is a statistical tool for analyzing methylated DNA immunoprecipitation profiles...
- Bayes factorBayes factorIn statistics, the use of Bayes factors is a Bayesian alternative to classical hypothesis testing. Bayesian model comparison is a method of model selection based on Bayes factors.-Definition:...
- Cromwell's ruleCromwell's ruleCromwell's rule, named by statistician Dennis Lindley, states that one should avoid using prior probabilities of 0 or 1, except when applied to statements that are logically true or false...
- Exchangeable random variables
- Gaussian process regression
- German tank problemGerman tank problemIn the statistical theory of estimation, estimating the maximum of a uniform distribution is a common illustration of differences between estimation methods...
- Hierarchical Bayes modelHierarchical Bayes modelThe hierarchical Bayes model is a method in modern Bayesian statistical inference. It is a framework for describing statistical models that can capture dependencies more realistically than non-hierarchical models....
- Influence diagramInfluence diagramAn influence diagram is a compact graphical and mathematical representation of a decision situation...
- Information theoryInformation theoryInformation theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
- Important publications in Bayesian statistics
- Minimum message lengthMinimum message lengthMinimum message length is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct...
- Minimum description lengthMinimum description lengthThe minimum description length principle is a formalization of Occam's Razor in which the best hypothesis for a given set of data is the one that leads to the best compression of the data. MDL was introduced by Jorma Rissanen in 1978...
- Maximum entropy thermodynamicsMaximum entropy thermodynamicsIn physics, maximum entropy thermodynamics views equilibrium thermodynamics and statistical mechanics as inference processes. More specifically, MaxEnt applies inference techniques rooted in Shannon information theory, Bayesian probability, and the principle of maximum entropy...
- Naive Bayes classifierNaive Bayes classifierA naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong independence assumptions...
- Occam's RazorOccam's razorOccam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
- Predictive inferencePredictive inferencePredictive inference is an approach to statistical inference that emphasizes the prediction of future observations based on past observations.Initially, predictive inference was based on observable parameters and it was the main purpose of studying probability, but it fell out of favor in the 20th...
- Prosecutor's fallacyProsecutor's fallacyThe prosecutor's fallacy is a fallacy of statistical reasoning made in law where the context in which the accused has been brought to court is falsely assumed to be irrelevant to judging how confident a jury can be in evidence against them with a statistical measure of doubt...
- Raven paradoxRaven paradoxThe Raven paradox, also known as Hempel's paradox or Hempel's ravens is a paradox proposed by the German logician Carl Gustav Hempel in the 1940s to illustrate a problem where inductive logic violates intuition...
- Robust Bayes analysisRobust Bayes analysisRobust Bayes analysis, also called Bayesian sensitivity analysis, investigates the robustness of answers from a Bayesian analysis to uncertainty about the precise details of the analysis. An answer is robust if it does not depend sensitively on the assumptions and calculation inputs on which it is...
- The Wisdom of CrowdsThe Wisdom of CrowdsThe Wisdom of Crowds: Why the Many Are Smarter Than the Few and How Collective Wisdom Shapes Business, Economies, Societies and Nations, published in 2004, is a book written by James Surowiecki about the aggregation of information in groups, resulting in decisions that, he argues, are often better...
Elementary
The following books are listed in ascending order of probabilistic sophistication:- Kruschke, John K. "Doing Bayesian Data Analysis: A Tutorial with R and BUGS" Academic Press/Elsevier ISBN 9780123814852
- Bolstad, William M. (2007) Introduction to Bayesian Statistics: Second Edition, John Wiley ISBN 0-471-27020-2
- Winkler, Robert L, Introduction to Bayesian Inference and Decision, 2nd Edition (2003) ISBN 0-9647938-4-9
- Lee, Peter M. Bayesian Statistics: An Introduction. Second Edition. (1997). ISBN 0-340-67785-6.
- Pole, Andy, West, Mike and Harrison, P. Jeff. Applied Bayesian Forecasting and Time Series Analysis, Chapman-Hall/Taylor Francis, 1994
Intermediate or Advanced
- Bolstad, William M. (2010) Understanding Computational Bayesian Statistics, John Wiley ISBN 0-470-04609-8
- Bretthorst, G. Larry, 1988, Bayesian Spectrum Analysis and Parameter Estimation in Lecture Notes in Statistics, 48, Springer-Verlag, New York, New York
- DeGroot, Morris H.Morris H. DeGroot-Biography:Born in Scranton, Pennsylvania, DeGroot graduated from Roosevelt University and earned master's and doctor's degrees from the University of Chicago. DeGroot joined Carnegie Mellon in 1957 and became a University Professor, the school's highest faculty position.He wrote three books,...
, Optimal Statistical Decisions. Wiley Classics Library. 2004. (Originally published (1970) by McGraw-Hill.) ISBN 0-471-68029-X. - Jaynes, E.T. (1998) Probability Theory: The Logic of Science. (On-line)
- O'Hagan, A. and Forster, J. (2003) Kendall's Advanced Theory of Statistics, Volume 2B: Bayesian Inference. Arnold, New York. ISBN 0-340-52922-9.
- Glenn Shafer and Pearl, JudeaJudea PearlJudea Pearl is a computer scientist and philosopher, best known for developing the probabilistic approach to artificial intelligence and the development of Bayesian networks ....
, eds. (1988) Probabilistic Reasoning in Intelligent Systems, San Mateo, CA: Morgan Kaufmann. - West, Mike, and Harrison, P. Jeff, Bayesian Forecasting and Dynamic Models, Springer-Verlag, 1997 (2nd ed.)
External links
- Bayesian Statistics summary from Scholarpedia.
- A nice on-line introductory tutorial to Bayesian probability from Queen Mary University of London
- An Intuitive Explanation of Bayesian Reasoning "Bayes' Theorem for the curious and bewildered; an excruciatingly gentle introduction by Eliezer YudkowskyEliezer YudkowskyEliezer Shlomo Yudkowsky is an American artificial intelligence researcher concerned with the singularity and an advocate of friendly artificial intelligence, living in Redwood City, California.- Biography :...
" - Paul Graham. "A Plan for Spam" (exposition of a popular approach for spam classification)
- Commentary on Regina versus Adams
- Mathematical notes on Bayesian statistics and Markov chain Monte Carlo
- Bayesian Rating/Ranking How to implement Bayes' Theorem for online rating and ranking systems
- Bayesian reading list, categorized and annotated. Designed for cognitive science; maintained by Tom Griffiths.
- Stanford Encyclopedia of Philosophy: Inductive Logic a comprehensive Bayesian treatment of Inductive Logic and Confirmation Theory
- Bayesian Confirmation Theory An extensive presentation of Bayesian Confirmation Theory
- What is Bayesian Learning?

