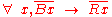Raven paradox
Encyclopedia
The Raven paradox, also known as Hempel's paradox or Hempel's ravens is a paradox
proposed by the German
logician Carl Gustav Hempel
in the 1940s to illustrate a problem where inductive logic violates intuition
. It reveals the fundamental problem of induction
.
.jpg)
 Hempel describes the paradox in terms of the hypothesis
Hempel describes the paradox in terms of the hypothesis
:
In strict logic
al terms, via the Law of Implication, this statement is equivalent to:
It should be clear that in all circumstances where (2) is true, (1) is also true; and likewise, in all circumstances where (2) is false (i.e. if a world is imagined in which something that was not black, yet was a raven, existed), (1) is also false. This establishes logical equivalence
.
Given a general statement such as all ravens are black, a form of the same statement would be generally considered that refers to a specific observable instance of the general class to constitute evidence for that general statement. For example,
is evidence supporting the hypothesis that all ravens are black.
The paradox arises when this same process is applied to statement (2). On sighting a green apple, one can observe:
By the same reasoning, this statement is evidence that (2) everything that is not black is not a raven. But since (as above) this statement is logically equivalent to (1) all ravens are black, it follows that the sight of a green apple is evidence supporting the notion that all ravens are black. This conclusion seems paradoxical, because it implies that information has been gained about ravens by looking at an apple.
and
can be combined to reach the seemingly paradoxical conclusion:
A resolution to the paradox must therefore either accept (PC) or reject
(EC) or reject (NC) or reject both. A satisfactory resolution should also explain
why there naively appears to be a paradox. Solutions which
accept the paradoxical conclusion can do this by presenting a
proposition which we intuitively know to be false but which
is easily confused with (PC), while solutions which reject (EC)
or (NC) should present a proposition which we intuitively know
to be true but which is easily confused with (EC) or (NC).
He illustrates this with the example of the generalization "All sodium salts burn yellow", and asks us to consider the observation which occurs when somebody holds a piece of pure ice in a colorless flame which does not turn yellow:
conclusion that the observation of a green apple provides
evidence that all ravens are black but to argue that the
amount of confirmation provided is very small, due to
the large discrepancy between the number of ravens and
the number of non-black objects. According to this resolution,
the conclusion appears paradoxical because we intuitively estimate the
amount of evidence provided by the observation of a green apple
to be zero, when it is in fact non-zero but extremely small.
I J Good's presentation of this
argument in 1960 is perhaps the best known, and variations of the argument have been popular ever
since
although it had been presented in 1958 and
early forms of the argument appeared as early as 1940.
Good's argument involves calculating the weight of evidence
provided by the observation of a black raven or a white shoe in favor of the hypothesis that all the ravens in a collection of objects are black. The weight of evidence is the logarithm of the Bayes factor
, which in this case is simply the factor by which the odds
of the hypothesis changes when the observation is made. The argument goes as follows:
Many of the proponents of this resolution and variants of it have
been advocates of Bayesian probability, and it is now commonly called
the Bayesian Solution, although, as Chihara
observes, "there is no such thing as the Bayesian solution. There
are many different 'solutions' that Bayesians have put forward
using Bayesian techniques." Noteworthy approaches using Bayesian
techniques include
Earman,
Eells,
Gibson,
Hosaisson-Lindenbaum,
Howson and Urbach,
Mackie, and
Hintikka, who claims that his approach
is "more Bayesian than the so-called 'Bayesian solution' of the same
paradox." Bayesian approaches which make use of Carnap's theory of inductive inference include
Humburg, Maher,
and Fitelson et al. Vranas introduced
the term "Standard Bayesian Solution" to avoid confusion.
In order to reach (ii), he appeals to Carnap's theory of inductive
probability, which is (from the Bayesian point of view) a way of assigning
prior probabilities which naturally implements induction. According to
Carnap's theory, the posterior probability, , that an object,
, that an object,
 , will have a predicate,
, will have a predicate,  , after the evidence
, after the evidence
 has been observed, is:
has been observed, is:
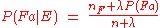
where is the initial probability that
is the initial probability that  has
has
the predicate ;
;  is the number of objects which
is the number of objects which
have been examined (according to the available evidence );
);
 is the number of examined objects which turned out to have the predicate
is the number of examined objects which turned out to have the predicate  , and
, and  is a constant which measures resistance to generalization.
is a constant which measures resistance to generalization.
If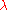 is close to zero,
is close to zero,  will be very
will be very
close to one after a single observation of an object which turned out to have the predicate ,
,
while if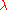 is much larger than
is much larger than  ,
,  will
will
be very close to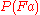 regardless of the fraction of observed
regardless of the fraction of observed
objects which had the predicate .
.
Using this Carnapian approach, Maher identifies a proposition which we intuitively
(and correctly) know to be false, but which we easily confuse with the paradoxical conclusion. The proposition in question
is the proposition that observing non-ravens tells us about the color of ravens.
While this is intuitively false and is also false according to Carnap's theory
of induction, observing non-ravens (according to that same theory) causes us
to reduce our estimate of the total number of ravens, and thereby reduces
the estimated number of possible counterexamples to the rule that all ravens
are black.
Hence, from the Bayesian-Carnapian point of view, the observation of a non-raven
does not tell us anything about the color of ravens, but it tells us about
the prevalence of ravens, and supports "All ravens are black" by reducing
our estimate of the number of ravens which might not be black.
in particular has centred on the relevance of background knowledge.
Surprisingly, Maher shows that, for a large class of possible configurations of background knowledge, the observation of a non-black non-raven provides exactly the same amount of confirmation as the observation of a black raven. The configurations of background knowledge which he considers are those which are provided by a sample proposition, namely a proposition which is a conjunction
of atomic propositions, each of which ascribes a single predicate to a single individual, with no two atomic propositions involving the same individual. Thus, a proposition of the form "A is a black raven and B is a white shoe" can be considered a sample proposition by taking "black raven" and "white shoe" to be predicates.
Maher's proof appears to contradict the result of the Bayesian argument, which was that the observation of a non-black non-raven provides much less evidence than the observation of a black raven. The reason is that the background knowledge which Good and others use can not be expressed in the form of a sample proposition - in particular, variants of the standard Bayesian approach often suppose (as Good did in the argument quoted above) that the total numbers of ravens, non-black objects and/or the total number of objects, are known quantities. Maher comments that, "The reason we think there are more non-black things than ravens is because that has been true of the things we have observed to date. Evidence of this kind can be represented by a sample proposition. But ... given any sample proposition as background evidence, a non-black non-raven confirms A just as strongly as a black raven does ... Thus my analysis suggests that this response to the paradox [i.e. the Standard Bayesian one] cannot be correct."
Fitelson et al. examined the conditions under which the
observation of a non-black non-raven provides less evidence than the observation
of a black raven. They show that, if is an object selected at random,
is an object selected at random,  is the proposition that the object is black, and
is the proposition that the object is black, and  is the proposition that the object is a raven, then the condition:
is the proposition that the object is a raven, then the condition:
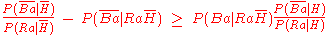
is sufficient for the observation of a non-black non-raven to provide less
evidence than the observation of a black raven. Here, a line over a
proposition indicates the logical negation of that proposition.
This condition does not tell us how large the difference
in the evidence provided is, but a later calculation in the same paper
shows that the weight of evidence provided by a black raven exceeds
that provided by a non-black non-raven by about
 . This is equal to the amount of
. This is equal to the amount of
additional information (in bits, if the base of the logarithm is 2) which
is provided when a raven of unknown color is discovered to be black,
given the hypothesis that not all ravens are black.
Fitelson et al. explain that:
The authors point out that their analysis is completely
consistent with the supposition that a non-black non-raven
provides an extremely small amount of evidence although
they do not attempt to prove it; they merely calculate the difference between
the amount of evidence that a black raven provides and the amount of evidence
that a non-black non-raven provides.
of background knowledge with respect to which the observation of a black raven
decreases the probability that all ravens are black:
Good concludes that the white shoe is a "red herring": Sometimes even a black raven
can constitute evidence against the hypothesis that all ravens are black, so
the fact that the observation of a white shoe can support it is not surprising and
not worth attention. Nicod's criterion is false, according to Good, and so the
paradoxical conclusion does not follow.
Hempel rejected this as a solution to the paradox, insisting that the proposition 'c is a raven and is black' must be considered "by itself and without reference to any other information", and pointing out that it "... was emphasized in section 5.2(b) of my article in Mind ... that the very appearance of paradoxicality in cases like that of the white shoe results in part from a failure to observe this maxim."
The question which then arises is whether the paradox is to be understood in the context of absolutely no background information (as Hempel suggests), or in the context of the background information which we actually possess regarding ravens and black objects, or with regard to all possible configurations of background information.
Good had shown that, for some configurations of background knowledge, Nicod's criterion
is false (provided that we are willing to equate "inductively support" with
"increase the probability of" - see below). The possibility remained that, with
respect to our actual configuration of knowledge, which is very different from
Good's example, Nicod's criterion might still be true and so we could still
reach the paradoxical conclusion. Hempel, on the other hand, insists that
it is our background knowledge itself which is the red herring, and that
we should consider induction with respect to a condition of perfect ignorance.
proposition "All ravens are black" is highly probable when it is highly
probable that there are no ravens. Good had used this fact before to respond
to Hempel's insistence that Nicod's criterion was to be understood to hold
in the absence of background information:
This, according to Good, is as close as one can reasonably expect to get to
a condition of perfect ignorance, and it appears that Nicod's condition is still
false. Maher made Good's argument more precise by using Carnap's theory of induction
to formalize the notion that if there is one raven, then it is likely
that there are many.
Maher's argument considers a universe of exactly two objects, each of which
is very unlikely to be a raven (a one in a thousand chance) and reasonably
unlikely to be black (a one in ten chance). Using Carnap's formula for induction,
he finds that the probability that all ravens are black decreases from 0.9985
to 0.8995 when it is discovered that one of the two objects is a black raven.
Maher concludes that not only is the paradoxical conclusion true, but
that Nicod's criterion is false in the absence of background knowledge
(except for the knowledge that the number of objects in the universe
is two and that ravens are less likely than black things).
lies in the recognition that certain predicates, which he
called natural kind
s, have a distinguished status with respect
to induction. This can be illustrated with Nelson Goodman
's
example of the predicate grue. An object is grue
if it is blue before (say) 2015 and green afterwards. Clearly, we
expect objects which were blue before 2015 to remain blue afterwards,
but we do not expect the objects which were found to be grue before
2015 to be grue afterwards. Quine's explanation is that "blue" is
a natural kind; a privileged predicate which can be used for induction,
while "grue" is not a natural kind and using induction with it leads
to error.
This suggests a resolution to the paradox - Nicod's criterion is
true for natural kinds, such as "blue" and "black", but is false
for artificially contrived predicates, such as "grue" or "non-raven".
The paradox arises, according to this resolution, because we implicitly
interpret Nicod's criterion as applying to all predicates when in fact
it only applies to natural kinds.
Another approach which favours specific predicates over others
was taken by Hintikka. Hintikka was motivated
to find a Bayesian approach to the paradox which did not make use
of knowledge about the relative frequencies of ravens and black things.
Arguments concerning relative frequencies, he contends, cannot always
account for the perceived irrelevance of evidence consisting of
observations of objects of type A for the purposes of learning
about objects of type not-A.
His argument can be illustrated by rephrasing the paradox using
predicates other than "raven" and "black". For example, "All men
are tall" is equivalent to "All short people are women", and so
observing that a randomly selected person is a short woman should
provide evidence that all men are tall. Despite the fact that
we lack background knowledge to indicate that there are dramatically
fewer men than short people, we still find ourselves inclined to
reject the conclusion. Hintikka's example is: "... a generalization
like 'no material bodies are infinitely divisible' seems to be completely
unaffected by questions concerning immaterial entities, independently
of what one thinks of the relative frequencies of material and
immaterial entities in one's universe of discourse."
His solution is to introduce an order into the
set of predicates. When the logical system is equipped with this order,
it is possible to restrict the scope of a generalization such as
"All ravens are black" so that it applies to ravens only and not to
non-black things, since the order privileges ravens over non-black things.
As he puts it:
took an approach to the paradox which incorporates
Karl Popper
's view that scientific hypotheses are never really confirmed,
only falsified.
The approach begins by noting that the observation of a black raven does not prove that "All ravens are black" but it falsifies the contrary hypothesis, "No ravens are black". A non-black non-raven, on the other hand, is consistent with both "All ravens are black" and with "No ravens are black". As the authors put it:
Selective confirmation violates the equivalence condition since
a black raven selectively confirms "All ravens are black" but
not "All non-black things are non-ravens".
an example of an interpretation of "provides evidence in favor of"
which does not coincide with "increase the probability of".
This must be a general feature of all resolutions which reject the
equivalence condition, since logically equivalent propositions must
always have the same probability.
It is impossible for the observation
of a black raven to increase the probability of the proposition
"All ravens are black" without causing exactly the same
change to the probability that "All non-black things are non-ravens".
If an observation inductively supports the former but not the
latter, then "inductively support" must refer to something other
than changes in the probabilities of propositions. A possible loophole
is to interpret "All" as "Nearly all" - "Nearly all ravens are black"
is not equivalent to "Nearly all non-black things are non-ravens", and
these propositions can have very different probabilities.
This raises the broader question of the relation of probability
theory to inductive reasoning. Karl Popper
argued that probability theory alone cannot
account for induction. His argument involves splitting a hypothesis,
 , into a part which is deductively entailed by the
, into a part which is deductively entailed by the
evidence, , and another part. This can be done in two
, and another part. This can be done in two
ways.
First, consider the splitting:

where ,
,  and
and  are
are
probabilistically independent: and
and
so on. The condition which is necessary for such a splitting
of H and E to be possible is , that is,
, that is,
that is probabilistically supported by
is probabilistically supported by  .
.
Popper's observation is that the part, , of
, of 
which receives support from actually follows deductively
actually follows deductively
from , while the part of
, while the part of  which does not
which does not
follow deductively from receives no support at all from
receives no support at all from
 - that is,
- that is,  .
.
Second, the splitting:
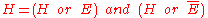
separates into
into 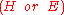 , which as
, which as
Popper says, "is the logically strongest part of
(or of the content of ) that follows [deductively]
) that follows [deductively]
from ," and
," and  , which,
, which,
he says, "contains all of that goes beyond
that goes beyond  ."
."
He continues:
theory
of hypothesis testing considers how to decide whether to
accept or reject a hypothesis, rather than what
probability to assign to the hypothesis. From this point of view,
the hypothesis that "All ravens are black" is not accepted
gradually, as its probability increases towards one when more
and more observations are made, but is accepted in a single action as the result of evaluating the data which has already been collected. As Neyman and Pearson put it:
According to this approach, it is not necessary to assign any
value to the probability of a hypothesis, although one must
certainly take into account the probability of the data
given the hypothesis, or given a competing hypothesis, when deciding
whether to accept or to reject. The acceptance or rejection of a hypothesis
carries with it the risk of error
.
This contrasts with the Bayesian approach, which requires that the
hypothesis be assigned a prior probability, which is revised in the
light of the observed data to obtain the final probability of the
hypothesis. Within the Bayesian framework there is no risk of error
since hypotheses are not accepted or rejected; instead they are
assigned probabilities.
An analysis of the paradox from the orthodox point of view has been
performed, and leads to, among other insights, a rejection of the
equivalence condition:
not a raven", "Every Raven is black", and "Every non-black object is a non-raven."
They are therefore, by definition, logically equivalent. However, the three
propositions have different domains: the first proposition says something about "Every
object", while the second says something about "Every raven".
The first proposition is the only one whose domain is unrestricted ("all objects"),
so this is the only one which can be expressed in first order logic. It is
logically equivalent to:

and also to
where indicates the material conditional
indicates the material conditional
, according
to which "If then
then  " can be understood to mean "
" can be understood to mean " or
or  ".
".
It has been argued by several authors that material implication does not fully
capture the meaning of "If then
then  " (see the paradoxes of material implication
" (see the paradoxes of material implication
). "For every object, ,
,  is either
is either
black or not a raven" is true when there are no ravens. It is because of this
that "All ravens are black" is regarded as true when there are no ravens. Furthermore, the
arguments which Good and Maher used to criticize Nicod's criterion (see Good's Baby, above)
relied on this fact - that "All ravens are black" is highly probable when it is
highly probable that there are no ravens.
Some approaches to the paradox have sought to find other ways of interpreting "If then
then  " and "All
" and "All  are
are  " which would
" which would
eliminate the perceived equivalence between "All ravens are black" and "All non-black
things are non-ravens."
One such approach involves introducing a many-valued logic according to which "If then
then  " has the truth-value
" has the truth-value 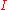 , meaning "Indeterminate" or "Inappropriate" when
, meaning "Indeterminate" or "Inappropriate" when  is false. In such a system, contraposition
is false. In such a system, contraposition
is not automatically allowed: "If then
then  " is not equivalent to "If
" is not equivalent to "If  then
then  ". Consequently, "All ravens are black" is not equivalent to "All non-black things are non-ravens".
". Consequently, "All ravens are black" is not equivalent to "All non-black things are non-ravens".
In this system, when contraposition occurs, the modality
of the conditional involved
changes from the indicative ("If that piece of butter has been heated to 32 C then it has melted") to the counterfactual
("If that piece of butter had been heated to 32 C then it would have melted"). According to this argument,
this removes the alleged equivalence which is necessary to conclude that yellow cows can inform us about ravens:
More recently, it has been suggested that "All ravens are black" and "All non-black things are non-ravens" can have different effects when accepted. The argument considers situations in which the total numbers or prevalences of ravens and black objects are unknown, but estimated. When the hypothesis "All ravens are black" is accepted,
according to the argument, the estimated number of black objects increases, while the
estimated number of ravens does not change.
It can be illustrated by considering the situation of two people who have identical information regarding ravens and black objects, and who have identical estimates of the
numbers of ravens and black objects. For concreteness, suppose that there are 100 objects
overall, and, according to the information available to the people involved, each object is just as likely to be a non-raven as it is to be a raven, and just as likely to be black as it is to be non-black:

and the propositions are independent for different
are independent for different
objects ,
,  and so on. Then the estimated number
and so on. Then the estimated number
of ravens is 50; the estimated number of black things is 50; the estimated
number of black ravens is 25, and the estimated number of non-black ravens
(counterexamples to the hypotheses) is 25.
One of the people performs a statistical test (e.g. a Neyman-Pearson
test or the comparison of the accumulated weight of evidence
to a threshold) of the hypothesis that "All ravens are black", while the other tests the hypothesis that "All non-black objects
are non-ravens". For simplicity, suppose that the evidence used for the test has nothing to do with the collection of 100 objects dealt with here. If the first person accepts the hypothesis that "All ravens are black" then, according to the argument, about 50 objects whose colors were previously in doubt (the ravens) are now thought to be black, while nothing different is thought about the remaining objects (the non-ravens). Consequently, he should estimate the number of black ravens at 50, the number of black non-ravens at 25 and the number of non-black non-ravens at 25. By specifying these changes, this argument explicitly restricts the domain of "All ravens are black" to ravens.
On the other hand, if the second person accepts the hypothesis that "All non-black objects are non-ravens", then the approximately 50 non-black objects about which it was uncertain whether each was a raven, will be thought to be non-ravens. At the same time, nothing different will be thought about the approximately 50 remaining objects (the black objects). Consequently, he should estimate the number of black ravens at 25, the number of black non-ravens at 25 and the number of non-black non-ravens at 50. According to this argument, since the two people disagree about their estimates after they have accepted the different hypotheses, accepting "All ravens are black" is not equivalent to accepting "All non-black things are non-ravens"; accepting the former means estimating more things to be black, while accepting the latter involves estimating more things to be non-ravens. Correspondingly, the argument goes, the former requires as evidence ravens which turn out to be black and the latter requires non-black things which turn out to be non-ravens.
 are
are  " presuppose that there are objects which are
" presuppose that there are objects which are  . This analysis has been applied to the raven paradox:
. This analysis has been applied to the raven paradox:
A modified logic can take account of existential presuppositions using the presuppositional operator, '*'. For example,
can denote "All ravens are black" while indicating that it is ravens and not non-black objects which are presupposed to exist in this example.
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
proposed by the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
logician Carl Gustav Hempel
Carl Gustav Hempel
Carl Gustav "Peter" Hempel was a philosopher of science and a major figure in 20th-century logical empiricism...
in the 1940s to illustrate a problem where inductive logic violates intuition
Intuition (knowledge)
Intuition is the ability to acquire knowledge without inference or the use of reason. "The word 'intuition' comes from the Latin word 'intueri', which is often roughly translated as meaning 'to look inside'’ or 'to contemplate'." Intuition provides us with beliefs that we cannot necessarily justify...
. It reveals the fundamental problem of induction
Problem of induction
The problem of induction is the philosophical question of whether inductive reasoning leads to knowledge. That is, what is the justification for either:...
.
The paradox
.jpg)

Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
:
- (1) All ravenRavenRaven is the common name given to several larger-bodied members of the genus Corvus—but in Europe and North America the Common Raven is normally implied...
s are blackBlackBlack is the color of objects that do not emit or reflect light in any part of the visible spectrum; they absorb all such frequencies of light...
.
In strict logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
al terms, via the Law of Implication, this statement is equivalent to:
- (2) Everything that is not black is not a raven.
It should be clear that in all circumstances where (2) is true, (1) is also true; and likewise, in all circumstances where (2) is false (i.e. if a world is imagined in which something that was not black, yet was a raven, existed), (1) is also false. This establishes logical equivalence
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
.
Given a general statement such as all ravens are black, a form of the same statement would be generally considered that refers to a specific observable instance of the general class to constitute evidence for that general statement. For example,
- (3) Nevermore, my pet raven, is black.
is evidence supporting the hypothesis that all ravens are black.
The paradox arises when this same process is applied to statement (2). On sighting a green apple, one can observe:
- (4) This green (and thus not black) thing is an apple (and thus not a raven).
By the same reasoning, this statement is evidence that (2) everything that is not black is not a raven. But since (as above) this statement is logically equivalent to (1) all ravens are black, it follows that the sight of a green apple is evidence supporting the notion that all ravens are black. This conclusion seems paradoxical, because it implies that information has been gained about ravens by looking at an apple.
Proposed resolutions
Two apparently reasonable premises:- The Equivalence Condition (EC): If a proposition, X, provides evidence in favor of another proposition Y, then X also provides evidence in favor of any proposition which is logically equivalent to Y.
and
- Nicod's Criterion (NC): A proposition of the form "All P are Q" is supported by the observation of a particular P which is Q.
can be combined to reach the seemingly paradoxical conclusion:
- (PC): The observation of a green apple provides evidence that all ravens are black.
A resolution to the paradox must therefore either accept (PC) or reject
(EC) or reject (NC) or reject both. A satisfactory resolution should also explain
why there naively appears to be a paradox. Solutions which
accept the paradoxical conclusion can do this by presenting a
proposition which we intuitively know to be false but which
is easily confused with (PC), while solutions which reject (EC)
or (NC) should present a proposition which we intuitively know
to be true but which is easily confused with (EC) or (NC).
Hempel's resolution
Hempel himself accepted the paradoxical conclusion, arguing that the reason the result appears paradoxical is because we possess prior information without which the observation of a non-black non-raven would indeed provide evidence that all ravens are black.He illustrates this with the example of the generalization "All sodium salts burn yellow", and asks us to consider the observation which occurs when somebody holds a piece of pure ice in a colorless flame which does not turn yellow:
The standard Bayesian solution
One of the most popular proposed resolutions is to accept theconclusion that the observation of a green apple provides
evidence that all ravens are black but to argue that the
amount of confirmation provided is very small, due to
the large discrepancy between the number of ravens and
the number of non-black objects. According to this resolution,
the conclusion appears paradoxical because we intuitively estimate the
amount of evidence provided by the observation of a green apple
to be zero, when it is in fact non-zero but extremely small.
I J Good's presentation of this
argument in 1960 is perhaps the best known, and variations of the argument have been popular ever
since
although it had been presented in 1958 and
early forms of the argument appeared as early as 1940.
Good's argument involves calculating the weight of evidence
Weight of evidence
Weight of evidence is a measure of evidence on one side of an issue as compared with the evidence on the other side of the issue, or to measure the evidence on multiple issues.Weight of evidence or WofE may be used in:...
provided by the observation of a black raven or a white shoe in favor of the hypothesis that all the ravens in a collection of objects are black. The weight of evidence is the logarithm of the Bayes factor
Bayes factor
In statistics, the use of Bayes factors is a Bayesian alternative to classical hypothesis testing. Bayesian model comparison is a method of model selection based on Bayes factors.-Definition:...
, which in this case is simply the factor by which the odds
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
of the hypothesis changes when the observation is made. The argument goes as follows:
- and this exceeds unity by only about r/(2N-2b) if N-b is large compared to r. Thus the weight of evidence provided by the sight of a white shoe is positive, but is small if the number of ravens is known to be small compared to the number of non-black objects.
Many of the proponents of this resolution and variants of it have
been advocates of Bayesian probability, and it is now commonly called
the Bayesian Solution, although, as Chihara
observes, "there is no such thing as the Bayesian solution. There
are many different 'solutions' that Bayesians have put forward
using Bayesian techniques." Noteworthy approaches using Bayesian
techniques include
Earman,
Eells,
Gibson,
Hosaisson-Lindenbaum,
Howson and Urbach,
Mackie, and
Hintikka, who claims that his approach
is "more Bayesian than the so-called 'Bayesian solution' of the same
paradox." Bayesian approaches which make use of Carnap's theory of inductive inference include
Humburg, Maher,
and Fitelson et al. Vranas introduced
the term "Standard Bayesian Solution" to avoid confusion.
The Carnapian approach
Maher accepts the paradoxical conclusion, and refines it:In order to reach (ii), he appeals to Carnap's theory of inductive
probability, which is (from the Bayesian point of view) a way of assigning
prior probabilities which naturally implements induction. According to
Carnap's theory, the posterior probability,
 , that an object,
, that an object, , will have a predicate,
, will have a predicate,  , after the evidence
, after the evidence has been observed, is:
has been observed, is: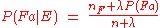
where
 is the initial probability that
is the initial probability that  has
hasthe predicate
 ;
;  is the number of objects which
is the number of objects whichhave been examined (according to the available evidence
 );
); is the number of examined objects which turned out to have the predicate
is the number of examined objects which turned out to have the predicate  , and
, and  is a constant which measures resistance to generalization.
is a constant which measures resistance to generalization.If
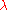 is close to zero,
is close to zero,  will be very
will be veryclose to one after a single observation of an object which turned out to have the predicate
 ,
,while if
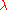 is much larger than
is much larger than  ,
,  will
willbe very close to
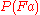 regardless of the fraction of observed
regardless of the fraction of observedobjects which had the predicate
 .
.Using this Carnapian approach, Maher identifies a proposition which we intuitively
(and correctly) know to be false, but which we easily confuse with the paradoxical conclusion. The proposition in question
is the proposition that observing non-ravens tells us about the color of ravens.
While this is intuitively false and is also false according to Carnap's theory
of induction, observing non-ravens (according to that same theory) causes us
to reduce our estimate of the total number of ravens, and thereby reduces
the estimated number of possible counterexamples to the rule that all ravens
are black.
Hence, from the Bayesian-Carnapian point of view, the observation of a non-raven
does not tell us anything about the color of ravens, but it tells us about
the prevalence of ravens, and supports "All ravens are black" by reducing
our estimate of the number of ravens which might not be black.
The role of background knowledge
Much of the discussion of the paradox in general and the Bayesian approachin particular has centred on the relevance of background knowledge.
Surprisingly, Maher shows that, for a large class of possible configurations of background knowledge, the observation of a non-black non-raven provides exactly the same amount of confirmation as the observation of a black raven. The configurations of background knowledge which he considers are those which are provided by a sample proposition, namely a proposition which is a conjunction
Conjunction
Conjunction can refer to:* Conjunction , an astronomical phenomenon* Astrological aspect, an aspect in horoscopic astrology* Conjunction , a part of speech** Conjunctive mood , same as subjunctive mood...
of atomic propositions, each of which ascribes a single predicate to a single individual, with no two atomic propositions involving the same individual. Thus, a proposition of the form "A is a black raven and B is a white shoe" can be considered a sample proposition by taking "black raven" and "white shoe" to be predicates.
Maher's proof appears to contradict the result of the Bayesian argument, which was that the observation of a non-black non-raven provides much less evidence than the observation of a black raven. The reason is that the background knowledge which Good and others use can not be expressed in the form of a sample proposition - in particular, variants of the standard Bayesian approach often suppose (as Good did in the argument quoted above) that the total numbers of ravens, non-black objects and/or the total number of objects, are known quantities. Maher comments that, "The reason we think there are more non-black things than ravens is because that has been true of the things we have observed to date. Evidence of this kind can be represented by a sample proposition. But ... given any sample proposition as background evidence, a non-black non-raven confirms A just as strongly as a black raven does ... Thus my analysis suggests that this response to the paradox [i.e. the Standard Bayesian one] cannot be correct."
Fitelson et al. examined the conditions under which the
observation of a non-black non-raven provides less evidence than the observation
of a black raven. They show that, if
 is an object selected at random,
is an object selected at random,  is the proposition that the object is black, and
is the proposition that the object is black, and  is the proposition that the object is a raven, then the condition:
is the proposition that the object is a raven, then the condition: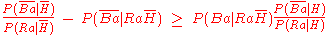
is sufficient for the observation of a non-black non-raven to provide less
evidence than the observation of a black raven. Here, a line over a
proposition indicates the logical negation of that proposition.
This condition does not tell us how large the difference
in the evidence provided is, but a later calculation in the same paper
shows that the weight of evidence provided by a black raven exceeds
that provided by a non-black non-raven by about
 . This is equal to the amount of
. This is equal to the amount ofadditional information (in bits, if the base of the logarithm is 2) which
is provided when a raven of unknown color is discovered to be black,
given the hypothesis that not all ravens are black.
Fitelson et al. explain that:
- Under normal circumstances,
 may be somewhere around 0.9 or 0.95; so
may be somewhere around 0.9 or 0.95; so 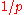 is somewhere around 1.11 or 1.05. Thus, it may appear that a single instance of a black raven does not yield much more support than would a non-black non-raven. However, under plausible conditions it can be shown that a sequence of
is somewhere around 1.11 or 1.05. Thus, it may appear that a single instance of a black raven does not yield much more support than would a non-black non-raven. However, under plausible conditions it can be shown that a sequence of  instances (i.e. of n black ravens, as compared to n non-black non-ravens) yields a ratio of likelihood ratios on the order of
instances (i.e. of n black ravens, as compared to n non-black non-ravens) yields a ratio of likelihood ratios on the order of 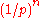 , which blows up significantly for large
, which blows up significantly for large  .
.
The authors point out that their analysis is completely
consistent with the supposition that a non-black non-raven
provides an extremely small amount of evidence although
they do not attempt to prove it; they merely calculate the difference between
the amount of evidence that a black raven provides and the amount of evidence
that a non-black non-raven provides.
The red herring
Good gives an exampleof background knowledge with respect to which the observation of a black raven
decreases the probability that all ravens are black:
- Suppose that we know we are in one or other of two worlds, and the hypothesis, H, under consideration is that all the ravens in our world are black. We know in advance that in one world there are a hundred black ravens, no non-black ravens, and a million other birds; and that in the other world there are a thousand black ravens, one white raven, and a million other birds. A bird is selected equiprobably at random from all the birds in our world. It turns out to be a black raven. This is strong evidence ... that we are in the second world, wherein not all ravens are black.
Good concludes that the white shoe is a "red herring": Sometimes even a black raven
can constitute evidence against the hypothesis that all ravens are black, so
the fact that the observation of a white shoe can support it is not surprising and
not worth attention. Nicod's criterion is false, according to Good, and so the
paradoxical conclusion does not follow.
Hempel rejected this as a solution to the paradox, insisting that the proposition 'c is a raven and is black' must be considered "by itself and without reference to any other information", and pointing out that it "... was emphasized in section 5.2(b) of my article in Mind ... that the very appearance of paradoxicality in cases like that of the white shoe results in part from a failure to observe this maxim."
The question which then arises is whether the paradox is to be understood in the context of absolutely no background information (as Hempel suggests), or in the context of the background information which we actually possess regarding ravens and black objects, or with regard to all possible configurations of background information.
Good had shown that, for some configurations of background knowledge, Nicod's criterion
is false (provided that we are willing to equate "inductively support" with
"increase the probability of" - see below). The possibility remained that, with
respect to our actual configuration of knowledge, which is very different from
Good's example, Nicod's criterion might still be true and so we could still
reach the paradoxical conclusion. Hempel, on the other hand, insists that
it is our background knowledge itself which is the red herring, and that
we should consider induction with respect to a condition of perfect ignorance.
Good's baby
In his proposed resolution, Maher implicitly made use of the fact that theproposition "All ravens are black" is highly probable when it is highly
probable that there are no ravens. Good had used this fact before to respond
to Hempel's insistence that Nicod's criterion was to be understood to hold
in the absence of background information:
- ...imagine an infinitely intelligent newborn baby having built-in neural circuits enabling him to deal with formal logic, English syntax, and subjective probability. He might now argue, after defining a raven in detail, that it is extremely unlikely that there are any ravens, and therefore it is extremely likely that all ravens are black, that is, that
 is true. 'On the other hand', he goes on to argue, 'if there are ravens, then there is a reasonable chance that they are of a variety of colours. Therefore, if I were to discover that even a black raven exists I would consider
is true. 'On the other hand', he goes on to argue, 'if there are ravens, then there is a reasonable chance that they are of a variety of colours. Therefore, if I were to discover that even a black raven exists I would consider  to be less probable than it was initially.'
to be less probable than it was initially.'
This, according to Good, is as close as one can reasonably expect to get to
a condition of perfect ignorance, and it appears that Nicod's condition is still
false. Maher made Good's argument more precise by using Carnap's theory of induction
to formalize the notion that if there is one raven, then it is likely
that there are many.
Maher's argument considers a universe of exactly two objects, each of which
is very unlikely to be a raven (a one in a thousand chance) and reasonably
unlikely to be black (a one in ten chance). Using Carnap's formula for induction,
he finds that the probability that all ravens are black decreases from 0.9985
to 0.8995 when it is discovered that one of the two objects is a black raven.
Maher concludes that not only is the paradoxical conclusion true, but
that Nicod's criterion is false in the absence of background knowledge
(except for the knowledge that the number of objects in the universe
is two and that ravens are less likely than black things).
Distinguished predicates
Quine argued that the solution to the paradoxlies in the recognition that certain predicates, which he
called natural kind
Natural kind
In philosophy, a natural kind is a "natural" grouping, not an artificial one. Or, it is something that a set of things has in common which distinguishes it from other things as a real set rather than as a group of things arbitrarily lumped together by a person or group of people.If any natural...
s, have a distinguished status with respect
to induction. This can be illustrated with Nelson Goodman
Nelson Goodman
Henry Nelson Goodman was an American philosopher, known for his work on counterfactuals, mereology, the problem of induction, irrealism and aesthetics.-Career:...
's
example of the predicate grue. An object is grue
if it is blue before (say) 2015 and green afterwards. Clearly, we
expect objects which were blue before 2015 to remain blue afterwards,
but we do not expect the objects which were found to be grue before
2015 to be grue afterwards. Quine's explanation is that "blue" is
a natural kind; a privileged predicate which can be used for induction,
while "grue" is not a natural kind and using induction with it leads
to error.
This suggests a resolution to the paradox - Nicod's criterion is
true for natural kinds, such as "blue" and "black", but is false
for artificially contrived predicates, such as "grue" or "non-raven".
The paradox arises, according to this resolution, because we implicitly
interpret Nicod's criterion as applying to all predicates when in fact
it only applies to natural kinds.
Another approach which favours specific predicates over others
was taken by Hintikka. Hintikka was motivated
to find a Bayesian approach to the paradox which did not make use
of knowledge about the relative frequencies of ravens and black things.
Arguments concerning relative frequencies, he contends, cannot always
account for the perceived irrelevance of evidence consisting of
observations of objects of type A for the purposes of learning
about objects of type not-A.
His argument can be illustrated by rephrasing the paradox using
predicates other than "raven" and "black". For example, "All men
are tall" is equivalent to "All short people are women", and so
observing that a randomly selected person is a short woman should
provide evidence that all men are tall. Despite the fact that
we lack background knowledge to indicate that there are dramatically
fewer men than short people, we still find ourselves inclined to
reject the conclusion. Hintikka's example is: "... a generalization
like 'no material bodies are infinitely divisible' seems to be completely
unaffected by questions concerning immaterial entities, independently
of what one thinks of the relative frequencies of material and
immaterial entities in one's universe of discourse."
His solution is to introduce an order into the
set of predicates. When the logical system is equipped with this order,
it is possible to restrict the scope of a generalization such as
"All ravens are black" so that it applies to ravens only and not to
non-black things, since the order privileges ravens over non-black things.
As he puts it:
- If we are justified in assuming that the scope of the generalization 'All ravens are black' can be restricted to ravens, then this means that we have some outside information which we can rely on concerning the factual situation. The paradox arises from the fact that this information, which colors our spontaneous view of the situation, is not incorporated in the usual treatments of the inductive situation.
Selective confirmation
Scheffler and GoodmanGoodman
Goodman may refer to:People* Goodman Places* Goodman, Missouri, a US city* Goodman, Wisconsin, a US town* Goodman , Wisconsin, an US unincorporated community* Goodman, Mississippi, a US townOther...
took an approach to the paradox which incorporates
Karl Popper
Karl Popper
Sir Karl Raimund Popper, CH FRS FBA was an Austro-British philosopher and a professor at the London School of Economics...
's view that scientific hypotheses are never really confirmed,
only falsified.
The approach begins by noting that the observation of a black raven does not prove that "All ravens are black" but it falsifies the contrary hypothesis, "No ravens are black". A non-black non-raven, on the other hand, is consistent with both "All ravens are black" and with "No ravens are black". As the authors put it:
- ... the statement that all ravens are black is not merely satisfied by evidence of a black raven but is favored by such evidence, since a black raven disconfirms the contrary statement that all ravens are not black, i.e. satisfies its denial. A black raven, in other words, satisfies the hypothesis that all ravens are black rather than not: it thus selectively confirms that all ravens are black.
Selective confirmation violates the equivalence condition since
a black raven selectively confirms "All ravens are black" but
not "All non-black things are non-ravens".
Probabilistic or non-probabilistic induction
Scheffler and Goodman's concept of selective confirmation isan example of an interpretation of "provides evidence in favor of"
which does not coincide with "increase the probability of".
This must be a general feature of all resolutions which reject the
equivalence condition, since logically equivalent propositions must
always have the same probability.
It is impossible for the observation
of a black raven to increase the probability of the proposition
"All ravens are black" without causing exactly the same
change to the probability that "All non-black things are non-ravens".
If an observation inductively supports the former but not the
latter, then "inductively support" must refer to something other
than changes in the probabilities of propositions. A possible loophole
is to interpret "All" as "Nearly all" - "Nearly all ravens are black"
is not equivalent to "Nearly all non-black things are non-ravens", and
these propositions can have very different probabilities.
This raises the broader question of the relation of probability
theory to inductive reasoning. Karl Popper
Karl Popper
Sir Karl Raimund Popper, CH FRS FBA was an Austro-British philosopher and a professor at the London School of Economics...
argued that probability theory alone cannot
account for induction. His argument involves splitting a hypothesis,
 , into a part which is deductively entailed by the
, into a part which is deductively entailed by theevidence,
 , and another part. This can be done in two
, and another part. This can be done in twoways.
First, consider the splitting:

where
 ,
,  and
and  are
areprobabilistically independent:
 and
andso on. The condition which is necessary for such a splitting
of H and E to be possible is
 , that is,
, that is,that
 is probabilistically supported by
is probabilistically supported by  .
.Popper's observation is that the part,
 , of
, of 
which receives support from
 actually follows deductively
actually follows deductivelyfrom
 , while the part of
, while the part of  which does not
which does notfollow deductively from
 receives no support at all from
receives no support at all from - that is,
- that is,  .
.Second, the splitting:
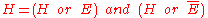
separates
 into
into 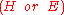 , which as
, which asPopper says, "is the logically strongest part of

(or of the content of
 ) that follows [deductively]
) that follows [deductively]from
 ," and
," and  , which,
, which,he says, "contains all of
 that goes beyond
that goes beyond  ."
."He continues:
- Does
 , in this case, provide any support for the factor
, in this case, provide any support for the factor  , which in the presence of
, which in the presence of  is alone needed to obtain
is alone needed to obtain  ? The answer is: No. It never does. Indeed,
? The answer is: No. It never does. Indeed,  countersupports
countersupports 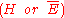 unless either
unless either  or
or 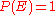 (which are possibilities of no interest). ...
(which are possibilities of no interest). ...
- This result is completely devastating to the inductive interpretation of the calculus of probability. All probabilistic support is purely deductive: that part of a hypothesis that is not deductively entailed by the evidence is always strongly countersupported by the evidence ... There is such a thing as probabilistic support; there might even be such a thing as inductive support (though we hardly think so). But the calculus of probability reveals that probabilistic support cannot be inductive support.
The orthodox approach
The orthodox Neyman-PearsonType I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
theory
of hypothesis testing considers how to decide whether to
accept or reject a hypothesis, rather than what
probability to assign to the hypothesis. From this point of view,
the hypothesis that "All ravens are black" is not accepted
gradually, as its probability increases towards one when more
and more observations are made, but is accepted in a single action as the result of evaluating the data which has already been collected. As Neyman and Pearson put it:
- Without hoping to know whether each separate hypothesis is true or false, we may search for rules to govern our behaviour with regard to them, in following which we insure that, in the long run of experience, we shall not be too often wrong.
According to this approach, it is not necessary to assign any
value to the probability of a hypothesis, although one must
certainly take into account the probability of the data
given the hypothesis, or given a competing hypothesis, when deciding
whether to accept or to reject. The acceptance or rejection of a hypothesis
carries with it the risk of error
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
.
This contrasts with the Bayesian approach, which requires that the
hypothesis be assigned a prior probability, which is revised in the
light of the observed data to obtain the final probability of the
hypothesis. Within the Bayesian framework there is no risk of error
since hypotheses are not accepted or rejected; instead they are
assigned probabilities.
An analysis of the paradox from the orthodox point of view has been
performed, and leads to, among other insights, a rejection of the
equivalence condition:
- It seems obvious that one cannot both accept the hypothesis that all P's are Q and also reject the contrapositive, i.e. that all non-Q's are non-P. Yet it is easy to see that on the Neyman-Pearson theory of testing, a test of "All P's are Q" is not necessarily a test of "All non-Q's are non-P" or vice versa. A test of "All P's are Q" requires reference to some alternative statistical hypothesis of the form
 of all P's are Q,
of all P's are Q,  , whereas a test of "All non-Q's are non-P" requires reference to some statistical alternative of the form
, whereas a test of "All non-Q's are non-P" requires reference to some statistical alternative of the form  of all non-Q's are non-P,
of all non-Q's are non-P, 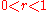 . But these two sets of possible alternatives are different ... Thus one could have a test of
. But these two sets of possible alternatives are different ... Thus one could have a test of  without having a test of its contrapositive.
without having a test of its contrapositive.
Rejecting material implication
The following propositions all imply one another: "Every object is either black ornot a raven", "Every Raven is black", and "Every non-black object is a non-raven."
They are therefore, by definition, logically equivalent. However, the three
propositions have different domains: the first proposition says something about "Every
object", while the second says something about "Every raven".
The first proposition is the only one whose domain is unrestricted ("all objects"),
so this is the only one which can be expressed in first order logic. It is
logically equivalent to:

and also to
where
 indicates the material conditional
indicates the material conditionalMaterial conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
, according
to which "If
 then
then  " can be understood to mean "
" can be understood to mean " or
or  ".
".It has been argued by several authors that material implication does not fully
capture the meaning of "If
 then
then  " (see the paradoxes of material implication
" (see the paradoxes of material implicationParadoxes of material implication
The paradoxes of material implication are a group of formulas which are truths of classical logic, but which are intuitively problematic. One of these paradoxes is the paradox of entailment....
). "For every object,
 ,
,  is either
is eitherblack or not a raven" is true when there are no ravens. It is because of this
that "All ravens are black" is regarded as true when there are no ravens. Furthermore, the
arguments which Good and Maher used to criticize Nicod's criterion (see Good's Baby, above)
relied on this fact - that "All ravens are black" is highly probable when it is
highly probable that there are no ravens.
Some approaches to the paradox have sought to find other ways of interpreting "If
 then
then  " and "All
" and "All  are
are  " which would
" which wouldeliminate the perceived equivalence between "All ravens are black" and "All non-black
things are non-ravens."
One such approach involves introducing a many-valued logic according to which "If
 then
then  " has the truth-value
" has the truth-value 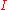 , meaning "Indeterminate" or "Inappropriate" when
, meaning "Indeterminate" or "Inappropriate" when  is false. In such a system, contraposition
is false. In such a system, contrapositionContraposition
In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
is not automatically allowed: "If
 then
then  " is not equivalent to "If
" is not equivalent to "If  then
then  ". Consequently, "All ravens are black" is not equivalent to "All non-black things are non-ravens".
". Consequently, "All ravens are black" is not equivalent to "All non-black things are non-ravens".In this system, when contraposition occurs, the modality
Modality
-Humanities:* In law: the basis of legal argumentation in United States constitutional law* In theology: Modality : the organization and structure of the church, as distinct from sodality or parachurch organizations...
of the conditional involved
changes from the indicative ("If that piece of butter has been heated to 32 C then it has melted") to the counterfactual
Counterfactual
Counterfactual may refer to:* Counterfactual conditional, a grammatical form * Counterfactual subjunctive, grammatical forms which in English are known as the past and pluperfect forms of the subjunctive mood* Counterfactual thinking* Counterfactual history* Alternate history, a literary genre*...
("If that piece of butter had been heated to 32 C then it would have melted"). According to this argument,
this removes the alleged equivalence which is necessary to conclude that yellow cows can inform us about ravens:
- In proper grammatical usage, a contrapositive argument ought not to be stated entirely in the indicative. Thus:
-
- From the fact that if this match is scratched it will light, it follows that if it does not light it was not scratched.
- is awkward. We should say:
-
- From the fact that if this match is scratched it will light, it follows that if it were not to light it would not have been scratched. ...
- One might wonder what effect this interpretation of the Law of Contraposition has on Hempel's paradox of confirmation. "If
 is a raven then
is a raven then  is black" is equivalent to "If
is black" is equivalent to "If  were not black then
were not black then  would not be a raven". Therefore whatever confirms the latter should also, by the Equivalence Condition, confirm the former. True, but yellow cows still cannot figure into the confirmation of "All ravens are black" because, in science, confirmation is accomplished by prediction, and predictions are properly stated in the indicative mood. It is senseless to ask what confirms a counterfactual.
would not be a raven". Therefore whatever confirms the latter should also, by the Equivalence Condition, confirm the former. True, but yellow cows still cannot figure into the confirmation of "All ravens are black" because, in science, confirmation is accomplished by prediction, and predictions are properly stated in the indicative mood. It is senseless to ask what confirms a counterfactual.
Differing results of accepting the hypotheses
Several commentators have observed that the propositions "All ravens are black" and "All non-black things are non-ravens" suggest different procedures for testing the hypotheses. E.g. Good writes:- As propositions the two statements are logically equivalent. But they have a different psychological effect on the experimenter. If he is asked to test whether all ravens are black he will look for a raven and then decide whether it is black. But if he is asked to test whether all non-black things are non-ravens he may look for a non-black object and then decide whether it is a raven.
More recently, it has been suggested that "All ravens are black" and "All non-black things are non-ravens" can have different effects when accepted. The argument considers situations in which the total numbers or prevalences of ravens and black objects are unknown, but estimated. When the hypothesis "All ravens are black" is accepted,
according to the argument, the estimated number of black objects increases, while the
estimated number of ravens does not change.
It can be illustrated by considering the situation of two people who have identical information regarding ravens and black objects, and who have identical estimates of the
numbers of ravens and black objects. For concreteness, suppose that there are 100 objects
overall, and, according to the information available to the people involved, each object is just as likely to be a non-raven as it is to be a raven, and just as likely to be black as it is to be non-black:

and the propositions
 are independent for different
are independent for differentobjects
 ,
,  and so on. Then the estimated number
and so on. Then the estimated numberof ravens is 50; the estimated number of black things is 50; the estimated
number of black ravens is 25, and the estimated number of non-black ravens
(counterexamples to the hypotheses) is 25.
One of the people performs a statistical test (e.g. a Neyman-Pearson
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
test or the comparison of the accumulated weight of evidence
Weight of evidence
Weight of evidence is a measure of evidence on one side of an issue as compared with the evidence on the other side of the issue, or to measure the evidence on multiple issues.Weight of evidence or WofE may be used in:...
to a threshold) of the hypothesis that "All ravens are black", while the other tests the hypothesis that "All non-black objects
are non-ravens". For simplicity, suppose that the evidence used for the test has nothing to do with the collection of 100 objects dealt with here. If the first person accepts the hypothesis that "All ravens are black" then, according to the argument, about 50 objects whose colors were previously in doubt (the ravens) are now thought to be black, while nothing different is thought about the remaining objects (the non-ravens). Consequently, he should estimate the number of black ravens at 50, the number of black non-ravens at 25 and the number of non-black non-ravens at 25. By specifying these changes, this argument explicitly restricts the domain of "All ravens are black" to ravens.
On the other hand, if the second person accepts the hypothesis that "All non-black objects are non-ravens", then the approximately 50 non-black objects about which it was uncertain whether each was a raven, will be thought to be non-ravens. At the same time, nothing different will be thought about the approximately 50 remaining objects (the black objects). Consequently, he should estimate the number of black ravens at 25, the number of black non-ravens at 25 and the number of non-black non-ravens at 50. According to this argument, since the two people disagree about their estimates after they have accepted the different hypotheses, accepting "All ravens are black" is not equivalent to accepting "All non-black things are non-ravens"; accepting the former means estimating more things to be black, while accepting the latter involves estimating more things to be non-ravens. Correspondingly, the argument goes, the former requires as evidence ravens which turn out to be black and the latter requires non-black things which turn out to be non-ravens.
Existential presuppositions
A number of authors have argued that propositions of the form "All are
are  " presuppose that there are objects which are
" presuppose that there are objects which are  . This analysis has been applied to the raven paradox:
. This analysis has been applied to the raven paradox:- ...
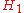 : "All ravens are black" and
: "All ravens are black" and 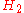 : "All nonblack things are nonravens" are not strictly equivalent ... due to their different existential presuppositions. Moreover, although
: "All nonblack things are nonravens" are not strictly equivalent ... due to their different existential presuppositions. Moreover, although 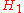 and
and 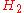 describe the same regularity - the nonexistence of nonblack ravens - they have different logical forms. The two hypotheses have different senses and incorporate different procedures for testing the regularity they describe.
describe the same regularity - the nonexistence of nonblack ravens - they have different logical forms. The two hypotheses have different senses and incorporate different procedures for testing the regularity they describe.
A modified logic can take account of existential presuppositions using the presuppositional operator, '*'. For example,
can denote "All ravens are black" while indicating that it is ravens and not non-black objects which are presupposed to exist in this example.
- ... the logical formLogical formIn logic, the logical form of a sentence or set of sentences is the form obtained by abstracting from the subject matter of its content terms or by regarding the content terms as mere placeholders or blanks on a form...
of each hypothesis distinguishes it with respect to its recommended type of supporting evidence: the possibly true substitution instances of each hypothesis relate to different types of objects. The fact that the two hypotheses incorporate different kinds of testing procedures is expressed in the formal language by prefixing the operator '*' to a different predicate. The presuppositional operator thus serves as a relevance operator as well. It is prefixed to the predicate ' is a raven' in
is a raven' in  because the objects relevant to the testing procedure incorporated in "All raven are black" include only ravens; it is prefixed to the predicate '
because the objects relevant to the testing procedure incorporated in "All raven are black" include only ravens; it is prefixed to the predicate ' is nonblack', in
is nonblack', in 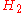 , because the objects relevant to the testing procedure incorporated in "All nonblack things are nonravens" include only nonblack things. ... Using Fregean terms: whenever their presuppositions hold, the two hypotheses have the same referentSense and referenceSinn and bedeutung are usually translated, respectively, as sense and reference. Two different aspects of some terms' meanings, a term's reference is the object that the term refers to, while the term's sense is the way that the term refers to that object.Sinn and bedeutung were introduced by...
, because the objects relevant to the testing procedure incorporated in "All nonblack things are nonravens" include only nonblack things. ... Using Fregean terms: whenever their presuppositions hold, the two hypotheses have the same referentSense and referenceSinn and bedeutung are usually translated, respectively, as sense and reference. Two different aspects of some terms' meanings, a term's reference is the object that the term refers to, while the term's sense is the way that the term refers to that object.Sinn and bedeutung were introduced by...
(truth-value), but different sensesSense and referenceSinn and bedeutung are usually translated, respectively, as sense and reference. Two different aspects of some terms' meanings, a term's reference is the object that the term refers to, while the term's sense is the way that the term refers to that object.Sinn and bedeutung were introduced by...
; that is, they express two different ways to determine that truth-value
External links
- "Hempel’s Ravens Paradox," PRIME (Platonic Realms Interactive Mathematics Encyclopedia). Retrieved November 29, 2010.