Type I and type II errors
Encyclopedia
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or "this product is not broken". An alternative hypothesis is the negation of null hypothesis, for example, "this person is not healthy", "this accused is guilty" or "this product is broken". The result of the test may be negative, relative to null hypothesis (not healthy, guilty, broken) or positive (healthy, not guilty, not broken). If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. Due to the statistical nature of a test, the result is never, except in very rare cases, free of error. Two types of error are distinguished:
type I error and type II error.
(H0). A type I error may be compared with a so called false positive in other test situations. Type I error can be viewed as the error of excessive credulity . In terms of folk tales, an investigator may be "crying wolf" (raising a false alarm) without a wolf in sight (H0: no wolf).
The rate of the type I error is called the size of the test and denoted by the Greek letter
(alpha). It usually equals the significance level
of a test. In the case of a simple null hypothesis
is the probability of a type I error. If the null hypothesis is composite, 
is the maximum (supremum) of the possible probabilities of a type I error.
. In terms of folk tales, an investigator may fail to see the wolf ("failing to raise an alarm"; see Aesop
's story of The Boy Who Cried Wolf
). Again, H0: no wolf.
The rate of the type II error is denoted by the Greek letter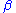
(beta) and related to the power
of a test (which equals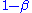
).
What we actually call type I or type II error depends directly on the null hypothesis. Negation of the null hypothesis causes type I and type II errors to switch roles.
The goal of the test is to determine if the null hypothesis can be rejected. A statistical test can either reject (prove false) or fail to reject (fail to prove false) a null hypothesis, but never prove it true (i.e., failing to reject a null hypothesis does not prove it true).
to toothpaste protects against cavities, the null hypothesis of no effect is tested. When the null hypothesis is true, i.e. there is indeed no effect, but the data give rise to reject this hypothesis, falsely suggesting that adding fluoride is effective against cavities, a type I error has occurred.
A type II error occurs when the null hypothesis is false, i.e. adding fluoride is actually effective against cavities, but the data are such that the null hypothesis cannot be rejected, failing to prove the existing effect.
In colloquial usage type I error can be thought of as "convicting an innocent person" and type II error "letting a guilty person go free".
Tabelarized relations between truth/falseness of the null hypothesis and outcomes of the test:
Hypothesis testing is the art of testing whether a variation between two sample distributions can be explained by chance or not. In many practical applications type I errors are more delicate than type II errors. In these cases, care is usually focused on minimizing the occurrence of this statistical error. Suppose, the probability for a type I error is 1% , then there is a 1% chance that the observed variation is not true. This is called the level of significance, denoted with the Greek letter
(alpha). While 1% might be an acceptable level of significance for one application, a different application can require a very different level. For example, the standard goal of six sigma
is to achieve precision to 4.5 standard deviations above or below the mean. This means that only 3.4 parts per million (0.00002941%) are allowed to be deficient in a normally distributed process.
. A false positive (with null hypothesis of health) in medicine causes unnecessary worry or treatment, while a false negative gives the patient the dangerous illusion of good health and the patient might not get an available treatment. A false positive in manufacturing quality control
(with a null hypothesis of a product being well-made), discards a product, which is actually well-made, while a false negative stamps a broken product as operational. A false positive (with null hypothesis of no effect) in scientific research suggest an effect, which is not actually there, while a false negative fails to detect an effect that is there.
Based on the real-life consequences of an error, one type may be more serious than the other. For example, NASA
engineers would prefer to throw out an electronic circuit that is really fine (null hypothesis H0: not broken; reality: not broken; action: thrown out; error: type I, false positive) than to use one on a spacecraft that is actually broken (null hypothesis H0: not broken; reality: broken; action: use it; error: type II, false negative). In that situation a type I error raises the budget, but a type II error would risk the entire mission.
Alternatively, criminal courts set high bar for proof and procedure
and sometimes release someone who is guilty (null hypothesis: innocent; reality: guilty; test find: not guilty; action: release; error: type II, false negative) rather than convict someone who is innocent (null hypothesis: innocent; reality: not guilty; test find: guilty; action: convict; error: type I, false positive). Each system makes its own choice regarding where to draw the line.
Minimizing errors of decision is not a simple issue; for any given sample size
the effort to reduce one type of error generally results in increasing the other type of error. The only way to minimize both types of error, without just improving the test, is to increase the sample size, and this may or may not be feasible.
(1894–1981) and Egon Pearson
(1895–1980), both eminent statistician
s, discussed the problems associated with "deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population" p. 1: and, as Florence Nightingale David
remarked, "it is necessary to remember the adjective 'random' [in the term 'random sample'] should apply to the method of drawing the sample and not to the sample itself".
They identified "two sources of error", namely: the error of rejecting a hypothesis that should have been accepted, and the error of accepting a hypothesis that should have been rejected.p.31
In 1930, they elaborated on these two sources of error, remarking that:
In 1933, they observed that these "problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis" (p.187). They also noted that, in deciding whether to accept or reject a particular hypothesis amongst a "set of alternative hypotheses" (p.201), it was easy to make an error:
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies "the hypothesis to be tested" (see, for example, p. 186).
In the same paperp. 190 they call these two sources of error, errors of type I and errors of type II respectively.
is the proportion of absent events that yield positive test outcomes, i.e., the conditional probability of a positive test result given an absent event.
The false positive rate is equal to the significance level. The specificity of the test is equal to 1 minus the false positive rate.
In statistical hypothesis testing
, this fraction is given the Greek letter
, and 
is defined as the specificity of the test. Increasing the specificity of the test lowers the probability of type I errors, but raises the probability of type II errors (false negatives that reject the alternative hypothesis when it is true). When developing detection algorithms or tests, a balance must be chosen between risks of false negatives and false positives. Usually there is a threshold of how close a match to a given sample must be achieved before the algorithm reports a match. The higher this threshold, the more false negatives and the fewer false positives.
In statistical hypothesis testing
, this fraction is given the letter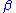
. The "power
" (or the "sensitivity
") of the test is equal to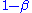
.
in order to determine whether or not a "speculative hypothesis
" concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called "null hypothesis" that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the "alternative hypothesis" (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson's convention of representing "the hypothesis to be tested" (or "the hypothesis to be nullified") with the expression H0 has led to circumstances where many understand the term "the null hypothesis" as meaning "the nil hypothesis" – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that "the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the 'problem of distribution,' of which the test of significance is the solution." As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.
The extent to which the test in question shows that the "speculated hypothesis" has (or has not) been nullified is called its significance level
; and the higher the significance level, the less likely it is that the phenomena in question could have been produced by chance alone. British statistician Sir Ronald Aylmer Fisher
(1890–1962) stressed that the "null hypothesis":
The key concept of Bayes' theorem is that the true rates of false positives and false negatives are not a function of the accuracy of the test alone, but also the actual rate or frequency
of occurrence within the test population; and, often, the more powerful issue is the actual rates of the condition within the sample being tested.
None of these proposed categories have met with any sort of wide acceptance. The following is a brief account of some of these proposals.
an additional type III error is often defined: type III (δ): asking the wrong question and using the wrong null hypothesis
.
, making a humorous aside at the end of her 1947 paper, suggested that, in the case of her own research, perhaps Neyman and Pearson's "two sources of error" could be extended to a third:
http://www.umass.edu/wsp/statistics/tales/mosteller.html argued that a "third kind of error" was required to describe circumstances he had observed, namely:
, proposed a different kind of error to stand beside "the first and second types of error in the theory of testing hypotheses". Kimball defined this new "error of the third kind" as being "the error committed by giving the right answer to the wrong problem" (1957, p. 134).
Mathematician Richard Hamming
(1915–1998) expressed his view that "It is better to solve the right problem the wrong way than to solve the wrong problem the right way".
Harvard economist Howard Raiffa
describes an occasion when he, too, "fell into the trap of working on the wrong problem" (1968, pp. 264–265).Note that Raiffa, from his imperfect recollection, incorrectly attributed this "error of the third kind" to John Tukey
(1915–2000).
They defined type III errors as either "the error ... of having solved the wrong problem ... when one should have solved the right problem" or "the error ... [of] choosing the wrong problem representation ... when one should have ... chosen the right problem representation" (1974), p. 383.
In the 2009 book Dirty rotten strategies by Ian I. Mitroff and Abraham Silvers described type III and type IV errors providing many examples of both developing good answers to the wrong questions (III) and deliberately selecting the wrong questions for intensive and skilled investigation (IV). Most of the examples have nothing to do with statistics, many being problems of public policy or business decisions.
A threshold value can be varied to make the test more restrictive or more sensitive; with the more restrictive tests increasing the risk of rejecting true positives, and the more sensitive tests increasing the risk of accepting false positives.
, computer insecurity
). Moulton (1983), stresses the importance of:
A false negative occurs when a spam
email is not detected as spam, but is classified as "non-spam". A low number of false negatives is an indicator of the efficiency of "spam filtering" methods.
. The incorrect detection may be due to heuristics or to an incorrect virus signature in a database. Similar problems can occur with antitrojan or antispyware software.
s of all kinds often create false positives. Optical character recognition
(OCR) software may detect an "a" where there are only some dots that appear to be an "a" to the algorithm being used.
that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes (see explosive detection
, metal detector
.)
The ratio of false positives (identifying an innocent traveller as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value
of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a high statistical sensitivity
but low statistical specificity
(one that allows minimal false negatives in return for a high rate of false positives).
, facial recognition
or iris
recognition, is susceptible to type I and type II errors. The null hypothesis is that the input does identify someone in the searched list of people, so:
If the system is designed to rarely match suspects then the probability of type II errors can be called the "False Alarm
Rate". On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
and testing
:
For example, most States in the USA require newborns to be screened for phenylketonuria
and hypothyroidism
, among other congenital disorder
s. Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.In relation to this newborn screening, recent studies have shown that there are more than 12 times more false positives than correct screens (Gambrill, 2006. http://www.nlm.nih.gov/medlineplus/news/fullstory_34471.html)
The simple blood tests used to screen possible blood donors
for HIV
and hepatitis
have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography
. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10 year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands
, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power
of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
ing.
False negatives may provide a falsely reassuring message to patients and physicians that disease is absent, when it is actually present. This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress test
s to detect coronary atherosclerosis
, even though cardiac stress test
s are known to only detect limitations of coronary artery blood flow due to advanced stenosis
.
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10%, is used to test a population with a true occurrence rate of 70%, many of the "negatives" detected by the test will be false. (See Bayes' theorem)
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening
. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the "positives" detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes' theorem.
or ghost
phenomena seen in images and such, when there is another plausible explanation. When observing a photograph, recording, or some other evidence that appears to have a paranormal origin – in this usage, a false positive is a disproven piece of media "evidence" (image, movie, audio recording, etc.) that actually has a normal explanation.Several sites provide examples of false positives, including The Atlantic Paranormal Society (TAPS) and Moorestown Ghost Research.
type I error and type II error.
Type I error
A type I error, also known as an error of the first kind, is the wrong decision that is made when a test rejects a true null hypothesisNull hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
(H0). A type I error may be compared with a so called false positive in other test situations. Type I error can be viewed as the error of excessive credulity . In terms of folk tales, an investigator may be "crying wolf" (raising a false alarm) without a wolf in sight (H0: no wolf).
The rate of the type I error is called the size of the test and denoted by the Greek letter
(alpha). It usually equals the significance levelStatistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
of a test. In the case of a simple null hypothesis
is the probability of a type I error. If the null hypothesis is composite, is the maximum (supremum) of the possible probabilities of a type I error.Type II error
A type II error, also known as an error of the second kind, is the wrong decision that is made when a test fails to reject a false null hypothesis. A type II error may be compared with a so-called false negative in other test situations. Type II error can be viewed as the error of excessive skepticismSkepticism
Skepticism has many definitions, but generally refers to any questioning attitude towards knowledge, facts, or opinions/beliefs stated as facts, or doubt regarding claims that are taken for granted elsewhere...
. In terms of folk tales, an investigator may fail to see the wolf ("failing to raise an alarm"; see Aesop
Aesop
Aesop was a Greek writer credited with a number of popular fables. Older spellings of his name have included Esop and Isope. Although his existence remains uncertain and no writings by him survive, numerous tales credited to him were gathered across the centuries and in many languages in a...
's story of The Boy Who Cried Wolf
The Boy Who Cried Wolf
The Boy Who Cried Wolf, is one of Aesop's Fables, numbered 210 in the Perry Index. From it is derived the English idiom 'to cry wolf', meaning to give a false alarm.-The fable and its history:...
). Again, H0: no wolf.
The rate of the type II error is denoted by the Greek letter
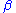(beta) and related to the powerStatistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
of a test (which equals
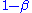).What we actually call type I or type II error depends directly on the null hypothesis. Negation of the null hypothesis causes type I and type II errors to switch roles.
The goal of the test is to determine if the null hypothesis can be rejected. A statistical test can either reject (prove false) or fail to reject (fail to prove false) a null hypothesis, but never prove it true (i.e., failing to reject a null hypothesis does not prove it true).
Example
As it is conjectured that adding fluorideFluoride
Fluoride is the anion F−, the reduced form of fluorine when as an ion and when bonded to another element. Both organofluorine compounds and inorganic fluorine containing compounds are called fluorides. Fluoride, like other halides, is a monovalent ion . Its compounds often have properties that are...
to toothpaste protects against cavities, the null hypothesis of no effect is tested. When the null hypothesis is true, i.e. there is indeed no effect, but the data give rise to reject this hypothesis, falsely suggesting that adding fluoride is effective against cavities, a type I error has occurred.
A type II error occurs when the null hypothesis is false, i.e. adding fluoride is actually effective against cavities, but the data are such that the null hypothesis cannot be rejected, failing to prove the existing effect.
In colloquial usage type I error can be thought of as "convicting an innocent person" and type II error "letting a guilty person go free".
Tabelarized relations between truth/falseness of the null hypothesis and outcomes of the test:
| Null hypothesis (H0) is true | Null hypothesis (H0) is false | |
|---|---|---|
| Reject null hypothesis | Type I error False positive |
Correct outcome True Positive |
| Fail to reject null hypothesis | Correct outcome True Negative |
Type II error False negative |
Understanding Type I and Type II errors
From the Bayesian point of view, a type I error is one that looks at information that should not substantially change one's prior estimate of probability, but does. A type II error is that one looks at information which should change one's estimate, but does not. (Though the null hypothesis is not quite the same thing as one's prior estimate, it is, rather, one's pro forma prior estimate.)Hypothesis testing is the art of testing whether a variation between two sample distributions can be explained by chance or not. In many practical applications type I errors are more delicate than type II errors. In these cases, care is usually focused on minimizing the occurrence of this statistical error. Suppose, the probability for a type I error is 1% , then there is a 1% chance that the observed variation is not true. This is called the level of significance, denoted with the Greek letter
(alpha). While 1% might be an acceptable level of significance for one application, a different application can require a very different level. For example, the standard goal of six sigmaSix Sigma
Six Sigma is a business management strategy originally developed by Motorola, USA in 1986. , it is widely used in many sectors of industry.Six Sigma seeks to improve the quality of process outputs by identifying and removing the causes of defects and minimizing variability in manufacturing and...
is to achieve precision to 4.5 standard deviations above or below the mean. This means that only 3.4 parts per million (0.00002941%) are allowed to be deficient in a normally distributed process.
Consequences of type I and type II errors
Both types of errors are problems for individuals, corporations, and data analysisData analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
. A false positive (with null hypothesis of health) in medicine causes unnecessary worry or treatment, while a false negative gives the patient the dangerous illusion of good health and the patient might not get an available treatment. A false positive in manufacturing quality control
Quality control
Quality control, or QC for short, is a process by which entities review the quality of all factors involved in production. This approach places an emphasis on three aspects:...
(with a null hypothesis of a product being well-made), discards a product, which is actually well-made, while a false negative stamps a broken product as operational. A false positive (with null hypothesis of no effect) in scientific research suggest an effect, which is not actually there, while a false negative fails to detect an effect that is there.
Based on the real-life consequences of an error, one type may be more serious than the other. For example, NASA
NASA
The National Aeronautics and Space Administration is the agency of the United States government that is responsible for the nation's civilian space program and for aeronautics and aerospace research...
engineers would prefer to throw out an electronic circuit that is really fine (null hypothesis H0: not broken; reality: not broken; action: thrown out; error: type I, false positive) than to use one on a spacecraft that is actually broken (null hypothesis H0: not broken; reality: broken; action: use it; error: type II, false negative). In that situation a type I error raises the budget, but a type II error would risk the entire mission.
Alternatively, criminal courts set high bar for proof and procedure
Beyond reasonable doubt
Beyond a reasonable doubt refers to the legal principle of reasonable doubt, the standard of proof required in most criminal cases.Beyond Reasonable Doubt may also refer to:...
and sometimes release someone who is guilty (null hypothesis: innocent; reality: guilty; test find: not guilty; action: release; error: type II, false negative) rather than convict someone who is innocent (null hypothesis: innocent; reality: not guilty; test find: guilty; action: convict; error: type I, false positive). Each system makes its own choice regarding where to draw the line.
Minimizing errors of decision is not a simple issue; for any given sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
the effort to reduce one type of error generally results in increasing the other type of error. The only way to minimize both types of error, without just improving the test, is to increase the sample size, and this may or may not be feasible.
Etymology
In 1928, Jerzy NeymanJerzy Neyman
Jerzy Neyman , born Jerzy Spława-Neyman, was a Polish American mathematician and statistician who spent most of his professional career at the University of California, Berkeley.-Life and career:...
(1894–1981) and Egon Pearson
Egon Pearson
Egon Sharpe Pearson, CBE FRS was the only son of Karl Pearson, and like his father, a leading British statistician....
(1895–1980), both eminent statistician
Statistician
A statistician is someone who works with theoretical or applied statistics. The profession exists in both the private and public sectors. The core of that work is to measure, interpret, and describe the world and human activity patterns within it...
s, discussed the problems associated with "deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population" p. 1: and, as Florence Nightingale David
Florence Nightingale David
Florence Nightingale David, also known as F. N. David was an English statistician, born in Ivington, Herefordshire, England...
remarked, "it is necessary to remember the adjective 'random' [in the term 'random sample'] should apply to the method of drawing the sample and not to the sample itself".
They identified "two sources of error", namely: the error of rejecting a hypothesis that should have been accepted, and the error of accepting a hypothesis that should have been rejected.p.31
In 1930, they elaborated on these two sources of error, remarking that:
-
- ...in testing hypotheses two considerations must be kept in view, (1) we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; (2) the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these "problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis" (p.187). They also noted that, in deciding whether to accept or reject a particular hypothesis amongst a "set of alternative hypotheses" (p.201), it was easy to make an error:
- ...[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,
- (II) we accept H0 when some alternative hypothesisHypothesisA hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
Hi is true.p.187
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies "the hypothesis to be tested" (see, for example, p. 186).
In the same paperp. 190 they call these two sources of error, errors of type I and errors of type II respectively.
False positive rate
The false positive rateFalse positive rate
When performing multiple comparisons in a statistical analysis, the false positive rate is the probability of falsely rejecting the null hypothesis for a particular test among all the tests performed...
is the proportion of absent events that yield positive test outcomes, i.e., the conditional probability of a positive test result given an absent event.
The false positive rate is equal to the significance level. The specificity of the test is equal to 1 minus the false positive rate.
In statistical hypothesis testing
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
, this fraction is given the Greek letter
, and is defined as the specificity of the test. Increasing the specificity of the test lowers the probability of type I errors, but raises the probability of type II errors (false negatives that reject the alternative hypothesis when it is true). When developing detection algorithms or tests, a balance must be chosen between risks of false negatives and false positives. Usually there is a threshold of how close a match to a given sample must be achieved before the algorithm reports a match. The higher this threshold, the more false negatives and the fewer false positives.False negative rate
The false negative rate is the proportion of events that are being tested for which yield negative test outcomes with the test, i.e., the conditional probability of a negative test result given that the event being looked for has taken place.In statistical hypothesis testing
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
, this fraction is given the letter
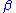. The "powerStatistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
" (or the "sensitivity
Sensitivity and specificity
Sensitivity and specificity are statistical measures of the performance of a binary classification test, also known in statistics as classification function. Sensitivity measures the proportion of actual positives which are correctly identified as such Sensitivity and specificity are statistical...
") of the test is equal to
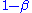.The null hypothesis
It is standard practice for statisticians to conduct testsStatistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
in order to determine whether or not a "speculative hypothesis
Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
" concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called "null hypothesis" that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the "alternative hypothesis" (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson's convention of representing "the hypothesis to be tested" (or "the hypothesis to be nullified") with the expression H0 has led to circumstances where many understand the term "the null hypothesis" as meaning "the nil hypothesis" – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that "the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the 'problem of distribution,' of which the test of significance is the solution." As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.
The extent to which the test in question shows that the "speculated hypothesis" has (or has not) been nullified is called its significance level
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
; and the higher the significance level, the less likely it is that the phenomena in question could have been produced by chance alone. British statistician Sir Ronald Aylmer Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
(1890–1962) stressed that the "null hypothesis":
- ... is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis. (1935, p.19)
Bayes' theorem
The probability that an observed positive result is a false positive (as contrasted with an observed positive result being a true positive) may be calculated using Bayes' theorem.The key concept of Bayes' theorem is that the true rates of false positives and false negatives are not a function of the accuracy of the test alone, but also the actual rate or frequency
Frequency (statistics)
In statistics the frequency of an event i is the number ni of times the event occurred in the experiment or the study. These frequencies are often graphically represented in histograms....
of occurrence within the test population; and, often, the more powerful issue is the actual rates of the condition within the sample being tested.
Various proposals for further extension
Since the paired notions of type I errors (or "false positives") and type II errors (or "false negatives") that were introduced by Neyman and Pearson are now widely used, their choice of terminology ("errors of the first kind" and "errors of the second kind"), has led others to suppose that certain sorts of mistake that they have identified might be an "error of the third kind", "fourth kind", etc.None of these proposed categories have met with any sort of wide acceptance. The following is a brief account of some of these proposals.
Systems Theory
In systems theorySystems theory
Systems theory is the transdisciplinary study of systems in general, with the goal of elucidating principles that can be applied to all types of systems at all nesting levels in all fields of research...
an additional type III error is often defined: type III (δ): asking the wrong question and using the wrong null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
.
David
Florence Nightingale David (1909–1993) http://www.agnesscott.edu/lriddle/women/david.htm a sometime colleague of both Neyman and Pearson at the University College LondonUniversity College London
University College London is a public research university located in London, United Kingdom and the oldest and largest constituent college of the federal University of London...
, making a humorous aside at the end of her 1947 paper, suggested that, in the case of her own research, perhaps Neyman and Pearson's "two sources of error" could be extended to a third:
- I have been concerned here with trying to explain what I believe to be the basic ideas [of my "theory of the conditional power functions"], and to forestall possible criticism that I am falling into error (of the third kind) and am choosing the test falsely to suit the significance of the sample. (1947, p.339)
Mosteller
In 1948, Frederick Mosteller (1916–2006)The 1981 President of the American Association for the Advancement of ScienceAmerican Association for the Advancement of Science
The American Association for the Advancement of Science is an international non-profit organization with the stated goals of promoting cooperation among scientists, defending scientific freedom, encouraging scientific responsibility, and supporting scientific education and science outreach for the...
http://www.umass.edu/wsp/statistics/tales/mosteller.html argued that a "third kind of error" was required to describe circumstances he had observed, namely:
- Type I error: "rejecting the null hypothesis when it is true".
- Type II error: "accepting the null hypothesis when it is false".
- Type III error: "correctly rejecting the null hypothesis for the wrong reason". (1948, p. 61)Compare with Kantian ethics, where it is not enough to do the right thing, but it must be done for the right reason, and Gettier problems, where "justified true belief" is not equated with knowledge.
Kaiser
According to Henry F. Kaiser (1927–1992), in his 1966 paper extended Mosteller's classification such that an error of the third kind entailed an incorrect decision of direction following a rejected two-tailed test of hypothesis. In his discussion (1966, pp. 162–163), Kaiser also speaks of α errors, β errors, and γ errors for type I, type II and type III errors respectively (C.O. Dellomos).Kimball
In 1957, Allyn W. Kimball, a statistician with the Oak Ridge National LaboratoryOak Ridge National Laboratory
Oak Ridge National Laboratory is a multiprogram science and technology national laboratory managed for the United States Department of Energy by UT-Battelle. ORNL is the DOE's largest science and energy laboratory. ORNL is located in Oak Ridge, Tennessee, near Knoxville...
, proposed a different kind of error to stand beside "the first and second types of error in the theory of testing hypotheses". Kimball defined this new "error of the third kind" as being "the error committed by giving the right answer to the wrong problem" (1957, p. 134).
Mathematician Richard Hamming
Richard Hamming
Richard Wesley Hamming was an American mathematician whose work had many implications for computer science and telecommunications...
(1915–1998) expressed his view that "It is better to solve the right problem the wrong way than to solve the wrong problem the right way".
Harvard economist Howard Raiffa
Howard Raiffa
Howard Raiffa is the Frank P. Ramsey Professor of Managerial Economics, a joint chair held by the Business School and the Kennedy School of Government at Harvard University...
describes an occasion when he, too, "fell into the trap of working on the wrong problem" (1968, pp. 264–265).Note that Raiffa, from his imperfect recollection, incorrectly attributed this "error of the third kind" to John Tukey
John Tukey
John Wilder Tukey ForMemRS was an American statistician.- Biography :Tukey was born in New Bedford, Massachusetts in 1915, and obtained a B.A. in 1936 and M.Sc. in 1937, in chemistry, from Brown University, before moving to Princeton University where he received a Ph.D...
(1915–2000).
Mitroff and Featheringham
In 1974, Ian Mitroff and Tom Featheringham extended Kimball's category, arguing that "one of the most important determinants of a problem's solution is how that problem has been represented or formulated in the first place".They defined type III errors as either "the error ... of having solved the wrong problem ... when one should have solved the right problem" or "the error ... [of] choosing the wrong problem representation ... when one should have ... chosen the right problem representation" (1974), p. 383.
In the 2009 book Dirty rotten strategies by Ian I. Mitroff and Abraham Silvers described type III and type IV errors providing many examples of both developing good answers to the wrong questions (III) and deliberately selecting the wrong questions for intensive and skilled investigation (IV). Most of the examples have nothing to do with statistics, many being problems of public policy or business decisions.
Raiffa
In 1969, the Harvard economist Howard Raiffa jokingly suggested "a candidate for the error of the fourth kind: solving the right problem too late" (1968, p. 264).Marascuilo and Levin
In 1970, L. A. Marascuilo and J. R. Levin proposed a "fourth kind of error" – a "type IV error" – which they defined in a Mosteller-like manner as being the mistake of "the incorrect interpretation of a correctly rejected hypothesis"; which, they suggested, was the equivalent of "a physician's correct diagnosis of an ailment followed by the prescription of a wrong medicine" (1970, p. 398).Usage examples
Statistical tests always involve a trade-off between: the acceptable level of false positives (in which a non-match is declared to be a match) and the acceptable level of false negatives (in which an actual match is not detected).A threshold value can be varied to make the test more restrictive or more sensitive; with the more restrictive tests increasing the risk of rejecting true positives, and the more sensitive tests increasing the risk of accepting false positives.
Inventory Control
An automated inventory control system that rejects high-quality goods of a consignment commits a type I Error while a system that accepts low-quality goods commits a type II Error.Computers
The notions of "false positives" and "false negatives" have a wide currency in the realm of computers and computer applications.Computer security
Security vulnerabilities are an important consideration in the task of keeping all computer data safe, while maintaining access to that data for appropriate users (see computer securityComputer security
Computer security is a branch of computer technology known as information security as applied to computers and networks. The objective of computer security includes protection of information and property from theft, corruption, or natural disaster, while allowing the information and property to...
, computer insecurity
Computer insecurity
Computer insecurity refers to the concept that a computer system is always vulnerable to attack, and that this fact creates a constant battle between those looking to improve security, and those looking to circumvent security.-Security and systems design:...
). Moulton (1983), stresses the importance of:
- avoiding the type I errors (or false positive) that classify authorized users as imposters.
- avoiding the type II errors (or false negatives) that classify imposters as authorized users (1983, p. 125).
Spam filtering
A false positive occurs when "spam filtering" or "spam blocking" techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery. While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.A false negative occurs when a spam
E-mail spam
Email spam, also known as junk email or unsolicited bulk email , is a subset of spam that involves nearly identical messages sent to numerous recipients by email. Definitions of spam usually include the aspects that email is unsolicited and sent in bulk. One subset of UBE is UCE...
email is not detected as spam, but is classified as "non-spam". A low number of false negatives is an indicator of the efficiency of "spam filtering" methods.
Malware
The term false positive is also used when antivirus software wrongly classifies an innocuous file as a virusComputer virus
A computer virus is a computer program that can replicate itself and spread from one computer to another. The term "virus" is also commonly but erroneously used to refer to other types of malware, including but not limited to adware and spyware programs that do not have the reproductive ability...
. The incorrect detection may be due to heuristics or to an incorrect virus signature in a database. Similar problems can occur with antitrojan or antispyware software.
Optical character recognition (OCR)
Detection algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s of all kinds often create false positives. Optical character recognition
Optical character recognition
Optical character recognition, usually abbreviated to OCR, is the mechanical or electronic translation of scanned images of handwritten, typewritten or printed text into machine-encoded text. It is widely used to convert books and documents into electronic files, to computerize a record-keeping...
(OCR) software may detect an "a" where there are only some dots that appear to be an "a" to the algorithm being used.
Security screening
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivitySensitivity (electronics)
The sensitivity of an electronic device, such as a communications system receiver, or detection device, such as a PIN diode, is the minimum magnitude of input signal required to produce a specified output signal having a specified signal-to-noise ratio, or other specified criteria.Sensitivity is...
that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes (see explosive detection
Explosive detection
Explosive detection is a non-destructive inspection process to determine whether a container contains explosive material. Explosive detection is commonly used at airports, ports and for border control.-Dogs:...
, metal detector
Metal detector
A metal detector is a device which responds to metal that may not be readily apparent.The simplest form of a metal detector consists of an oscillator producing an alternating current that passes through a coil producing an alternating magnetic field...
.)
The ratio of false positives (identifying an innocent traveller as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value
Positive predictive value
In statistics and diagnostic testing, the positive predictive value, or precision rate is the proportion of subjects with positive test results who are correctly diagnosed. It is a critical measure of the performance of a diagnostic method, as it reflects the probability that a positive test...
of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a high statistical sensitivity
Sensitivity and specificity
Sensitivity and specificity are statistical measures of the performance of a binary classification test, also known in statistics as classification function. Sensitivity measures the proportion of actual positives which are correctly identified as such Sensitivity and specificity are statistical...
but low statistical specificity
Sensitivity and specificity
Sensitivity and specificity are statistical measures of the performance of a binary classification test, also known in statistics as classification function. Sensitivity measures the proportion of actual positives which are correctly identified as such Sensitivity and specificity are statistical...
(one that allows minimal false negatives in return for a high rate of false positives).
Biometrics
Biometric matching, such as for fingerprintFingerprint
A fingerprint in its narrow sense is an impression left by the friction ridges of a human finger. In a wider use of the term, fingerprints are the traces of an impression from the friction ridges of any part of a human hand. A print from the foot can also leave an impression of friction ridges...
, facial recognition
Face
The face is a central sense organ complex, for those animals that have one, normally on the ventral surface of the head, and can, depending on the definition in the human case, include the hair, forehead, eyebrow, eyelashes, eyes, nose, ears, cheeks, mouth, lips, philtrum, temple, teeth, skin, and...
or iris
Iris (anatomy)
The iris is a thin, circular structure in the eye, responsible for controlling the diameter and size of the pupils and thus the amount of light reaching the retina. "Eye color" is the color of the iris, which can be green, blue, or brown. In some cases it can be hazel , grey, violet, or even pink...
recognition, is susceptible to type I and type II errors. The null hypothesis is that the input does identify someone in the searched list of people, so:
- the probability of type I errors is called the "False Reject Rate" (FRR) or False Non-match Rate (FNMR),
- while the probability of type II errors is called the "False Accept Rate" (FAR) or False Match Rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the "False Alarm
False Alarm
"False Alarm" is a song by the Los Angeles-based punk rock band The Bronx, released as the second single from their 2003 debut album The Bronx...
Rate". On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Medical screening
In the practice of medicine, there is a significant difference between the applications of screeningScreening (medicine)
Screening, in medicine, is a strategy used in a population to detect a disease in individuals without signs or symptoms of that disease. Unlike what generally happens in medicine, screening tests are performed on persons without any clinical sign of disease....
and testing
Medical test
A diagnostic test is any kind of medical test performed to aid in the diagnosis or detection of disease. For example:* to diagnose diseases, and preferably sub-classify it regarding, for example, severity and treatability...
:
- Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smearPap smearThe Papanicolaou test is a screening test used in to detect pre-cancerous and cancerous processes in the endocervical canal of the female reproductive system. Changes can be treated, thus preventing cervical cancer...
s). - Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most States in the USA require newborns to be screened for phenylketonuria
Phenylketonuria
Phenylketonuria is an autosomal recessive metabolic genetic disorder characterized by a mutation in the gene for the hepatic enzyme phenylalanine hydroxylase , rendering it nonfunctional. This enzyme is necessary to metabolize the amino acid phenylalanine to the amino acid tyrosine...
and hypothyroidism
Hypothyroidism
Hypothyroidism is a condition in which the thyroid gland does not make enough thyroid hormone.Iodine deficiency is the most common cause of hypothyroidism worldwide but it can be caused by other causes such as several conditions of the thyroid gland or, less commonly, the pituitary gland or...
, among other congenital disorder
Congenital disorder
A congenital disorder, or congenital disease, is a condition existing at birth and often before birth, or that develops during the first month of life , regardless of causation...
s. Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.In relation to this newborn screening, recent studies have shown that there are more than 12 times more false positives than correct screens (Gambrill, 2006. http://www.nlm.nih.gov/medlineplus/news/fullstory_34471.html)
The simple blood tests used to screen possible blood donors
Blood transfusion
Blood transfusion is the process of receiving blood products into one's circulation intravenously. Transfusions are used in a variety of medical conditions to replace lost components of the blood...
for HIV
HIV
Human immunodeficiency virus is a lentivirus that causes acquired immunodeficiency syndrome , a condition in humans in which progressive failure of the immune system allows life-threatening opportunistic infections and cancers to thrive...
and hepatitis
Hepatitis
Hepatitis is a medical condition defined by the inflammation of the liver and characterized by the presence of inflammatory cells in the tissue of the organ. The name is from the Greek hepar , the root being hepat- , meaning liver, and suffix -itis, meaning "inflammation"...
have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography
Mammography
Mammography is the process of using low-energy-X-rays to examine the human breast and is used as a diagnostic and a screening tool....
. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10 year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands
Netherlands
The Netherlands is a constituent country of the Kingdom of the Netherlands, located mainly in North-West Europe and with several islands in the Caribbean. Mainland Netherlands borders the North Sea to the north and west, Belgium to the south, and Germany to the east, and shares maritime borders...
, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing
False negatives and false positives are significant issues in medical testMedical test
A diagnostic test is any kind of medical test performed to aid in the diagnosis or detection of disease. For example:* to diagnose diseases, and preferably sub-classify it regarding, for example, severity and treatability...
ing.
False negatives may provide a falsely reassuring message to patients and physicians that disease is absent, when it is actually present. This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress test
Cardiac stress test
Cardiac stress test is a test used in medicine and cardiology to measure the heart's ability to respond to external stress in a controlled clinical environment....
s to detect coronary atherosclerosis
Atherosclerosis
Atherosclerosis is a condition in which an artery wall thickens as a result of the accumulation of fatty materials such as cholesterol...
, even though cardiac stress test
Cardiac stress test
Cardiac stress test is a test used in medicine and cardiology to measure the heart's ability to respond to external stress in a controlled clinical environment....
s are known to only detect limitations of coronary artery blood flow due to advanced stenosis
Stenosis
A stenosis is an abnormal narrowing in a blood vessel or other tubular organ or structure.It is also sometimes called a stricture ....
.
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10%, is used to test a population with a true occurrence rate of 70%, many of the "negatives" detected by the test will be false. (See Bayes' theorem)
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening
Screening (medicine)
Screening, in medicine, is a strategy used in a population to detect a disease in individuals without signs or symptoms of that disease. Unlike what generally happens in medicine, screening tests are performed on persons without any clinical sign of disease....
. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the "positives" detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes' theorem.
Paranormal investigation
The notion of a false positive is common in cases of paranormalParanormal
Paranormal is a general term that designates experiences that lie outside "the range of normal experience or scientific explanation" or that indicates phenomena understood to be outside of science's current ability to explain or measure...
or ghost
Ghost
In traditional belief and fiction, a ghost is the soul or spirit of a deceased person or animal that can appear, in visible form or other manifestation, to the living. Descriptions of the apparition of ghosts vary widely from an invisible presence to translucent or barely visible wispy shapes, to...
phenomena seen in images and such, when there is another plausible explanation. When observing a photograph, recording, or some other evidence that appears to have a paranormal origin – in this usage, a false positive is a disproven piece of media "evidence" (image, movie, audio recording, etc.) that actually has a normal explanation.Several sites provide examples of false positives, including The Atlantic Paranormal Society (TAPS) and Moorestown Ghost Research.
See also
- Detection theoryDetection theoryDetection theory, or signal detection theory, is a means to quantify the ability to discern between information-bearing energy patterns and random energy patterns that distract from the information Detection theory, or signal detection theory, is a means to quantify the ability to discern between...
- Egon PearsonEgon PearsonEgon Sharpe Pearson, CBE FRS was the only son of Karl Pearson, and like his father, a leading British statistician....
- False positive paradoxFalse positive paradoxThe false positive paradox is a statistical result where false positive tests are more probable than true positive tests, occurring when the overall population has a low incidence of a condition and the incidence rate is lower than the false positive rate...
- Family-wise error rate
- Information retrieval performance measures
- Negative information
- Neyman-Pearson lemma
- Null hypothesisNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
- Prosecutor's fallacyProsecutor's fallacyThe prosecutor's fallacy is a fallacy of statistical reasoning made in law where the context in which the accused has been brought to court is falsely assumed to be irrelevant to judging how confident a jury can be in evidence against them with a statistical measure of doubt...
- Prozone phenomenonProzone phenomenonThe prozone phenomenon is defined as a falsely negative test due to very high titers of antibody.Many laboratory tests rely on antigen-antibody interactions. The prozone phenomenon is said to be present when dilution of a previously negative sample leads to a positive test...
- Receiver operating characteristicReceiver operating characteristicIn signal detection theory, a receiver operating characteristic , or simply ROC curve, is a graphical plot of the sensitivity, or true positive rate, vs. false positive rate , for a binary classifier system as its discrimination threshold is varied...
- Sensitivity and specificitySensitivity and specificitySensitivity and specificity are statistical measures of the performance of a binary classification test, also known in statistics as classification function. Sensitivity measures the proportion of actual positives which are correctly identified as such Sensitivity and specificity are statistical...
- Statisticians' and engineers' cross-reference of statistical termsStatisticians' and engineers' cross-reference of statistical termsThe following terms are used by electrical engineers in statistical signal processing studies instead of typical statistician's terms.The following terms are used by electrical engineers in statistical signal processing studies instead of typical statistician's terms.The following terms are used by...
- Testing hypotheses suggested by the dataTesting hypotheses suggested by the dataIn statistics, hypotheses suggested by the data, if tested using the data set that suggested them, are likely to be accepted even when they are not true...
External links
- Bias and Confounding - presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh