
Minimum message length
Encyclopedia
Minimum message length is a formal information theory
restatement of Occam's Razor
: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct (where the message consists of a statement of the model, followed by a statement of data encoded concisely using that model). MML was invented by Chris Wallace
, first appearing in the seminal (Wallace and Boulton, 1968).
MML is intended not just as a theoretical construct, but as a technique that may be deployed in practice. It differs from the related concept of Kolmogorov complexity
in that it does not require use of a Turing-complete
language to model data. The relation between Strict MML (SMML) and Kolmogorov complexity
is outlined in Wallace and Dowe (1999a). Further, a variety of mathematical approximations to "Strict" MML can be used — see, e.g., Chapters 4 and 5 of Wallace (posthumous) 2005.
(1949) states that in an optimal code, the message length (in binary) of an event ,
, 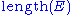 , where
, where  has probability
has probability 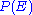 , is given by
, is given by 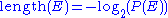 .
.
Bayes's theorem states that the probability of a hypothesis ( ) given evidence (
) given evidence ( ) is proportional to
) is proportional to 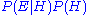 , which is just
, which is just 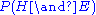 . We want the model (hypothesis) with the highest such probability. Therefore, we want the model which generates the shortest (two-part) encoding of the data. Since
. We want the model (hypothesis) with the highest such probability. Therefore, we want the model which generates the shortest (two-part) encoding of the data. Since 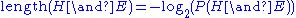 , the most probable model will have the shortest such message. The message breaks into two parts:
, the most probable model will have the shortest such message. The message breaks into two parts: 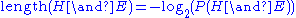 . The first is the length of the model, and the second is the length of the data, given the model.
. The first is the length of the model, and the second is the length of the data, given the model.
MML naturally and precisely trades model complexity for goodness of fit. A more complicated model takes longer to state (longer first part) but probably fits the data better (shorter second part). So, an MML metric won't choose a complicated model unless that model pays for itself.
Models for machine learning and data mining in functional programming, J. Functional Programming, 15(1), pp15-32, Jan. 2005 (MML, FP, and Haskell code).
[See also Comley and Dowe (2003), .pdf. Comley & Dowe (2003, 2005) are the first two papers on MML Bayesian nets using both discrete and continuous valued parameters.]
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
restatement of Occam's Razor
Occam's razor
Occam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct (where the message consists of a statement of the model, followed by a statement of data encoded concisely using that model). MML was invented by Chris Wallace
Chris Wallace (computer scientist)
Professor Christopher Stewart Wallace was an Australian computer scientist notable for having devised:...
, first appearing in the seminal (Wallace and Boulton, 1968).
MML is intended not just as a theoretical construct, but as a technique that may be deployed in practice. It differs from the related concept of Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
in that it does not require use of a Turing-complete
Turing completeness
In computability theory, a system of data-manipulation rules is said to be Turing complete or computationally universal if and only if it can be used to simulate any single-taped Turing machine and thus in principle any computer. A classic example is the lambda calculus...
language to model data. The relation between Strict MML (SMML) and Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
is outlined in Wallace and Dowe (1999a). Further, a variety of mathematical approximations to "Strict" MML can be used — see, e.g., Chapters 4 and 5 of Wallace (posthumous) 2005.
Definition
Shannon's A Mathematical Theory of CommunicationA Mathematical Theory of Communication
"A Mathematical Theory of Communication" is an influential 1948 article by mathematician Claude E. Shannon. As of November 2011, Google Scholar has listed more than 48,000 unique citations of the article and the later-published book version...
(1949) states that in an optimal code, the message length (in binary) of an event
 ,
, 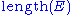 , where
, where  has probability
has probability 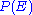 , is given by
, is given by 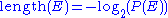 .
.Bayes's theorem states that the probability of a hypothesis (
 ) given evidence (
) given evidence ( ) is proportional to
) is proportional to 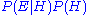 , which is just
, which is just 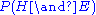 . We want the model (hypothesis) with the highest such probability. Therefore, we want the model which generates the shortest (two-part) encoding of the data. Since
. We want the model (hypothesis) with the highest such probability. Therefore, we want the model which generates the shortest (two-part) encoding of the data. Since 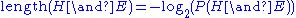 , the most probable model will have the shortest such message. The message breaks into two parts:
, the most probable model will have the shortest such message. The message breaks into two parts: 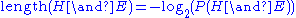 . The first is the length of the model, and the second is the length of the data, given the model.
. The first is the length of the model, and the second is the length of the data, given the model.MML naturally and precisely trades model complexity for goodness of fit. A more complicated model takes longer to state (longer first part) but probably fits the data better (shorter second part). So, an MML metric won't choose a complicated model unless that model pays for itself.
Continuous-valued parameters
One reason why a model might be longer would be simply because its various parameters are stated to greater precision, thus requiring transmission of more digits. Much of the power of MML derives from its handling of how accurately to state parameters in a model, and a variety of approximations that make this feasible in practice. This allows it to usefully compare, say, a model with many parameters imprecisely stated against a model with fewer parameters more accurately stated.Key features of MML
- MML can be used to compare models of different structure. For example, its earliest application was in finding mixture modelMixture modelIn statistics, a mixture model is a probabilistic model for representing the presence of sub-populations within an overall population, without requiring that an observed data-set should identify the sub-population to which an individual observation belongs...
s with the optimal number of classes. Adding extra classes to a mixture model will always allow the data to be fitted to greater accuracy, but according to MML this must be weighed against the extra bits required to encode the parameters defining those classes. - MML is a method of Bayesian model comparison. It gives every model a score.
- MML is scale-invariant and statistically invariant. Unlike many Bayesian selection methods, MML doesn't care if you change from measuring length to volume or from Cartesian co-ordinates to polar co-ordinates.
- MML is statistically consistent. For problems like the Neyman-Scott (1948) problem or factor analysis where the amount of data per parameter is bounded above, MML can estimate all parameters with statistical consistency.
- MML accounts for the precision of measurement. It uses the Fisher informationFisher informationIn mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
(in the Wallace-Freeman 1987 approximation, or other hyper-volumes in other approximations) to optimally discretize continuous parameters. Therefore the posterior is always a probability, not a probability density. - MML has been in use since 1968. MML coding schemes have been developed for several distributions, and many kinds of machine learners including unsupervised classification, decision trees and graphs, DNA sequences, Bayesian networkBayesian networkA Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
s, neural networks (one-layer only so far), image compression, image and function segmentation, etc.
See also
- Minimum description lengthMinimum description lengthThe minimum description length principle is a formalization of Occam's Razor in which the best hypothesis for a given set of data is the one that leads to the best compression of the data. MDL was introduced by Jorma Rissanen in 1978...
— a supposedly non-Bayesian alternative with a possibly different motivation, which was introduced 10 years later — for comparisons, see, e.g., (sec. 10.2 of Wallace (posthumous) 2005) and (sec. 11.4.3, pp272-273 of Comley and Dowe, 2005) and the special issue on Kolmogorov Complexity in the Computer Journal: Vol. 42, No. 4, 1999. - Kolmogorov complexityKolmogorov complexityIn algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
— absolute complexity (within a constant, depending on the particular choice of Universal Turing MachineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
); MML is typically a computable approximation (see Wallace and Dowe (1999a) below for elaboration) - Algorithmic information theoryAlgorithmic information theoryAlgorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information...
- Grammar inductionGrammar InductionGrammatical induction, also known as grammatical inference or syntactic pattern recognition, refers to the process in machine learning of learning a formal grammar from a set of observations, thus constructing a model which accounts for the characteristics of the observed objects...
External links
- Links to all Chris Wallace's known publications.
- C.S. WallaceChris Wallace (computer scientist)Professor Christopher Stewart Wallace was an Australian computer scientist notable for having devised:...
, Statistical and Inductive Inference by Minimum Message Length, Springer-Verlag (Information Science and Statistics), ISBN 0-387-23795-X, May 2005 - chapter headings, table of contents and sample pages. - A searchable database of Chris Wallace's publications.
- Minimum Message Length and Kolmogorov Complexity (by C.S. Wallace and D.L. Dowe, Computer Journal, Vol. 42, No. 4, 1999, pp270-283).
- History of MML, CSW's last talk.
- Message Length as an Effective Ockham's Razor in Decision Tree Induction, by S. Needham and D. Dowe, Proc. 8th International Workshop on AI and Statistics (2001), pp253-260. (Shows how Occam's razorOccam's razorOccam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
works fine when interpreted as MML.) - L.Allison,
Models for machine learning and data mining in functional programming, J. Functional Programming, 15(1), pp15-32, Jan. 2005 (MML, FP, and Haskell code).
- J.W.Comley and D.L. Dowe (2005), "Minimum Message Length, MDL and Generalised Bayesian Networks with Asymmetric Languages", Chapter 11 (pp265-294) in P. Grunwald, M. A. Pitt and I. J. Myung (ed.), Advances in Minimum Description Length: Theory and Applications, M.I.T. Press (MIT Press), April 2005, ISBN 0-262-07262-9.
[See also Comley and Dowe (2003), .pdf. Comley & Dowe (2003, 2005) are the first two papers on MML Bayesian nets using both discrete and continuous valued parameters.]
- Dowe, David L. (2010). MML, hybrid Bayesian network graphical models, statistical consistency, invariance and uniqueness, in Handbook of Philosophy of Science (Volume 7: Handbook of Philosophy of Statistics), Elsevier, ISBN: 978-0-444-51862-0, pp901-982.
- Minimum Message Length (MML), LA's MML introduction, (MML alt.).
- Minimum Message Length (MML), researchers and links.
- Another MML research website.
- Snob page for MML mixture modellingMixture modelIn statistics, a mixture model is a probabilistic model for representing the presence of sub-populations within an overall population, without requiring that an observed data-set should identify the sub-population to which an individual observation belongs...
. - MITECS: Chris Wallace wrote an entry on MML for MITECS. (Requires account)
- mikko.ps: Short introductory slides by Mikko Koivisto in Helsinki]
- Akaike information criterionAkaike information criterionThe Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
(AICAkaike information criterionThe Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
) method of model selectionModel selectionModel selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
, and a comparison with MML: D.L. Dowe, S. Gardner & G. Oppy (2007), "Bayes not Bust! Why Simplicity is no Problem for Bayesians", Brit. J. Philos. Sci., Vol. 58, Dec. 2007, pp709-754.

