
Posterior probability
Encyclopedia
In Bayesian statistics
, the posterior probability of a random event or an uncertain proposition is the conditional probability
that is assigned after the relevant evidence
is taken into account. Similarly, the posterior probability distribution is the distribution of an unknown quantity, treated as a random variable
, conditional on the evidence obtained from an experiment or survey.
belief that the probability distribution function
is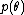 and an observation
and an observation  with the likelihood
with the likelihood 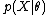 , then the posterior probability is defined as
, then the posterior probability is defined as

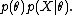
The posterior probability can be written in the memorable form as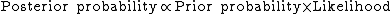 .
.
The event A is that the student observed is a girl, and the event B is that the student observed is wearing trousers. To compute P(A|B), we first need to know:
Given all this information, the probability of the observer having spotted a girl given that the observed student is wearing trousers can be computed by substituting these values in the formula:

given the value of another can be calculated with Bayes' theorem
by multiplying the prior probability distribution by the likelihood function
, and then dividing by the normalizing constant
, as follows:
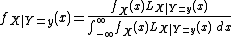
gives the posterior probability density function
for a random variable X given the data Y = y, where
.
While Statistical classification methods by definition generate posterior probabilities, Machine Learners usually supply membership values which do not induce any probabilistic confidence. It is desirable, to transform or re-scale membership values to class membership probabilities, since they are comparable and additionally easier applicable for post-processing.
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
, the posterior probability of a random event or an uncertain proposition is the conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
that is assigned after the relevant evidence
Scientific evidence
Scientific evidence has no universally accepted definition but generally refers to evidence which serves to either support or counter a scientific theory or hypothesis. Such evidence is generally expected to be empirical and properly documented in accordance with scientific method such as is...
is taken into account. Similarly, the posterior probability distribution is the distribution of an unknown quantity, treated as a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, conditional on the evidence obtained from an experiment or survey.
Definition
Let us have an a prioriA priori (statistics)
In statistics, a priori knowledge is prior knowledge about a population, rather than that estimated by recent observation. It is common in Bayesian inference to make inferences conditional upon this knowledge, and the integration of a priori knowledge is the central difference between the Bayesian...
belief that the probability distribution function
Probability distribution function
Depending upon which text is consulted, a probability distribution function is any of:* a probability distribution function,* a cumulative distribution function,* a probability mass function, or* a probability density function....
is
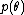 and an observation
and an observation  with the likelihood
with the likelihood 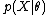 , then the posterior probability is defined as
, then the posterior probability is defined as

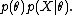
The posterior probability can be written in the memorable form as
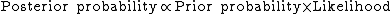 .
.Example
Suppose there is a mixed school having 60% boys and 40% girls as students. The girl students wear trousers or skirts in equal numbers; the boys all wear trousers. An observer sees a (random) student from a distance; all the observer can see is that this student is wearing trousers. What is the probability this student is a girl? The correct answer can be computed using Bayes' theorem.The event A is that the student observed is a girl, and the event B is that the student observed is wearing trousers. To compute P(A|B), we first need to know:
- P(A), or the probability that the student is a girl regardless of any other information. Since the observer sees a random student, meaning that all students have the same probability of being observed, and the percentage of girls among the students is 40%, this probability equals 0.4.
- P(A
' ), or the probability that the student is a boy regardless of any other information (A' is the complementary event to A). This is 60%, or 0.6. - P(B|A), or the probability of the student wearing trousers given that the student is a girl. As they are as likely to wear skirts as trousers, this is 0.5.
- P(B|A
' ), or the probability of the student wearing trousers given that the student is a boy. This is given as 1. - P(B), or the probability of a (randomly selected) student wearing trousers regardless of any other information. Since P(B) = P(B|A)P(A) + P(B|A
' )P(A' ), this is .
Given all this information, the probability of the observer having spotted a girl given that the observed student is wearing trousers can be computed by substituting these values in the formula:

Calculation
The posterior probability distribution of one random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
given the value of another can be calculated with Bayes' theorem
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
by multiplying the prior probability distribution by the likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
, and then dividing by the normalizing constant
Normalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
, as follows:
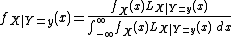
gives the posterior probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
for a random variable X given the data Y = y, where
-
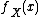 is the prior density of X,
is the prior density of X,
-
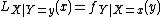 is the likelihood function as a function of x,
is the likelihood function as a function of x,
-
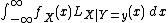 is the normalizing constant, and
is the normalizing constant, and
-
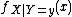 is the posterior density of X given the data Y = y.
is the posterior density of X given the data Y = y.
Classification
In classification posterior probabilities reflect the uncertainty of assessing an observation to particular class, see also Class membership probabilitiesClass membership probabilities
In general proplems of classification, class membership probabilities reflect the uncertainty with which a given indivual item can be assigned to any given class. Although statistical classification methods by definition generate such probabilities, applications of classification in machine...
.
While Statistical classification methods by definition generate posterior probabilities, Machine Learners usually supply membership values which do not induce any probabilistic confidence. It is desirable, to transform or re-scale membership values to class membership probabilities, since they are comparable and additionally easier applicable for post-processing.

