Hierarchical Bayes model - AbsoluteAstronomy.com

The hierarchical Bayes model is a method in modern Bayesian statistical inference

Bayesian inference

In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...

. It is a framework for describing statistical model

Statistical model

A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...

s that can capture dependencies more realistically than non-hierarchical models.

Given data

and parameters

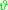, a simple Bayesian analysis

Bayesian statistics

Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...

starts with a prior probability

Prior probability

In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...

(prior)

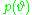and likelihood

Likelihood function

In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...

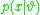to compute a posterior probability

Posterior probability

In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...

.

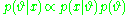Often the prior on

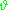depends in turn on other parameters

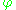that are not mentioned in the likelihood. So, the prior

must be replaced by a likelihood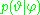

, and a prior

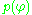on the newly introduced parameters

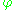is required, resulting in a posterior probability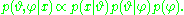

This is the simplest example of a hierarchical Bayes model.

The process may be repeated; for example, the parameters

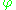may depend in turn on additional parameters

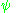, which will require their own prior. Eventually the process must terminate, with priors that do not depend on any other unmentioned parameters.

Examples

Suppose we have measured the quantities

each with normally distributed errors of known standard deviation

Standard deviation

Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...

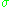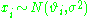
Suppose we are interested in estimating the

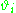. An approach would be to estimate the

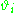using a maximum likelihood

Maximum likelihood

In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....

approach; since the observations are independent, the likelihood factorizes and the maximum likelihood estimate is simply

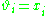
However, if the quantities are related, so that for example we may think that the individual

have themselves been drawn from an underlying distribution, then this relationship destroys the independence and suggests a more complex model, e.g.,

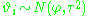
with improper priors

flat,

flat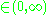

. When

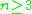, this is an identified model (i.e. there exists a unique solution for the model's parameters), and the posterior distributions of the individual

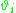will tend to move, or shrink
Shrinkage estimator
In statistics, a shrinkage estimator is an estimator that, either explicitly or implicitly, incorporates the effects of shrinkage. In loose terms this means that a naïve or raw estimate is improved by combining it with other information. The term relates to the notion that the improved estimate is...

away from the maximum likelihood estimates towards their common mean. This shrinkage is a typical behavior in hierarchical Bayes models.

Restrictions on priors

Some care is needed when choosing priors in a hierarchical model, particularly on scale variables at higher levels of the hierarchy such as the variable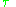

in the example. The usual priors such as the Jeffreys prior

Jeffreys prior

In Bayesian probability, the Jeffreys prior, named after Harold Jeffreys, is a non-informative prior distribution on parameter space that is proportional to the square root of the determinant of the Fisher information:...

often do not work, because the posterior distribution will be improper (not normalizable), and estimates made by minimizing the expected loss will be inadmissible

Admissible decision rule

In statistical decision theory, an admissible decision rule is a rule for making a decision such that there isn't any other rule that is always "better" than it, in a specific sense defined below....

Representation by directed acyclic graphs (DAGs)

A useful graphical tool for representing hierarchical Bayes models is the directed acyclic graph

Directed acyclic graph

In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...

, or DAG. In this diagram, the likelihood function is represented as the root of the graph; each prior is represented as a separate node pointing to the node that depends on it. In a simple Bayesian model, the data

are at the root of the diagram, representing the likelihood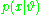

, and the variable

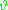is placed in a node that points to the root, as in the following diagram: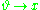

In the simplest hierarchical Bayes model, where

in turn depends on a new variable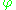

, a new node labelled

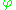is indicated, with an arrow pointed towards the node

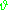, as in the equation below or the diagram at right. See also Bayesian network

Bayesian network

A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...

External links

A hierarchical Bayes Model for handling sample heterogeneity in classification problems, provides a classification model taking into consideration the uncertainty associated with measuring replicate samples.
Hierarchical Naive Bayes Model for handling sample uncertainty, shows how to perform classification and learning with continuous and discrete variables with replicated measurements.

Software:

JAGS, Just Another Gibbs Sampler.
OpenBUGS, further (open source) development of WinBUGS.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.