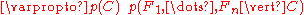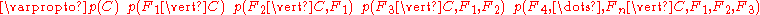Naive Bayes classifier
Encyclopedia
A naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem
with strong (naive) independence
assumptions. A more descriptive term for the underlying probability model would be "independent
feature model".
In simple terms, a naive Bayes classifier assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or absence) of any other feature, given the class variable. For example, a fruit may be considered to be an apple if it is red, round, and about 4" in diameter. Even if these features depend on each other or upon the existence of the other features, a naive Bayes classifier considers all of these properties to independently contribute to the probability that this fruit is an apple.
Depending on the precise nature of the probability model, naive Bayes classifiers can be trained very efficiently in a supervised learning
setting. In many practical applications, parameter estimation for naive Bayes models uses the method of maximum likelihood
; in other words, one can work with the naive Bayes model without believing in Bayesian probability
or using any Bayesian methods.
In spite of their naive design and apparently over-simplified assumptions, naive Bayes classifiers have worked quite well in many complex real-world situations. In 2004, analysis of the Bayesian classification problem has shown that there are some theoretical reasons for the apparently unreasonable efficacy
of naive Bayes classifiers. Still, a comprehensive comparison with other classification methods in 2006 showed that Bayes classification is outperformed by more current approaches, such as boosted trees or random forests.
An advantage of the naive Bayes classifier is that it only requires a small amount of training data to estimate the parameters (means and variances of the variables) necessary for classification. Because independent variables are assumed, only the variances of the variables for each class need to be determined and not the entire covariance matrix
.
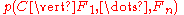
over a dependent class variable
with a small number of outcomes or classes, conditional on several feature variables 
through 
. The problem is that if the number of features 
is large or when a feature can take on a large number of values, then basing such a model on probability tables is infeasible. We therefore reformulate the model to make it more tractable.
Using Bayes' theorem
, we write
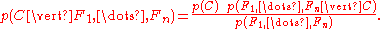
In plain English the above equation can be written as
In practice we are only interested in the numerator of that fraction, since the denominator does not depend on
and the values of the features 
are given, so that the denominator is effectively constant.
The numerator is equivalent to the joint probability model
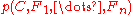
which can be rewritten as follows, using repeated applications of the definition of conditional probability
:
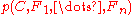
Now the "naive" conditional independence
assumptions come into play: assume that each feature
is conditionally independent
of every other feature
for 
. This means that
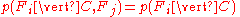
for
, and so the joint model can be expressed as
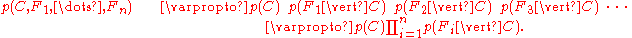
This means that under the above independence assumptions, the conditional distribution over the class variable
can be expressed like this:
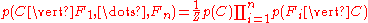
where
(the evidence) is a scaling factor dependent only on 
, i.e., a constant if the values of the feature variables are known.
Models of this form are much more manageable, since they factor into a so-called class prior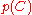
and independent probability distributions 
. If there are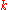 
classes and if a model for each 
can be expressed in terms of 
parameters, then the corresponding naive Bayes model has (k − 1) + n r k parameters. In practice, often 
(binary classification) and 
(Bernoulli variables as features) are common, and so the total number of parameters of the naive Bayes model is 
, where 
is the number of binary features used for classification and prediction
estimates of the probabilities. A class' prior may be calculated by assuming equiprobable classes (i.e., priors = 1 / (number of classes)), or by calculating an estimate for the class probability from the training set (i.e., (prior for a given class) = (number of samples in the class) / (total number of samples)). To estimate the parameters for a feature's distribution, one must assume a distribution or generate nonparametric models for the features from the training set. If one is dealing with continuous data, a typical assumption is that the continuous values associated with each class are distributed according to a Gaussian distribution.
For example, suppose the training data contains a continuous attribute,
. We first segment the data by the class, and then compute the mean and variance of 
in each class. Let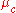 
be the mean of the values in 
associated with class c, and let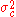 
be the variance of the values in 
associated with class c. Then, the probability of some value given a class,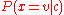 
, can be computed by plugging 
into the equation for a Normal distribution parameterized by 
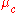and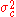 
. That is,
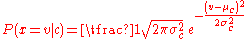
Another common technique for handling continuous values is to use binning to discretize
the values. In general, the distribution method is a better choice if there is a small amount of training data, or if the precise distribution of the data is known. The discretization method tends to do better if there is a large amount of training data because it will learn to fit the distribution of the data. Since naive Bayes is typically used when a large amount of data is available (as more computationally expensive models can generally achieve better accuracy), the discretization method is generally preferred over the distribution method.
.
combines this model with a decision rule
. One common rule is to pick the hypothesis that is most probable; this is known as the maximum a posteriori
or MAP decision rule. The corresponding classifier is the function
defined as follows:
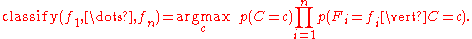
, such as the need for data sets that scale exponentially with the number of features. Like all probabilistic classifiers under the MAP decision rule, it arrives at the correct classification as long as the correct class is more probable than any other class; hence class probabilities do not have to be estimated very well. In other words, the overall classifier is robust enough to ignore serious deficiencies in its underlying naive probability model. Other reasons for the observed success of the naive Bayes classifier are discussed in the literature cited below.
The features include height, weight, and foot size.
The classifier created from the training set using a Gaussian distribution assumption would be:
Let's say we have equiprobable classes so P(male)= P(female) = 0.5. There was no identified reason for making this assumption so it may have been a bad idea. If we determine P(C) based on frequency in the training set, we happen to get the same answer.
We wish to determine which posterior is greater, male or female. For the classification as male the posterior is given by
For the classification as female the posterior is given by
The evidence (also termed normalizing constant) may be calculated since the sum of the posteriors equals one.
The evidence may be ignored since it is a positive constant. (Normal distributions are always positive.) We now determine the sex of the sample.
P(male) = 0.5
P(height | male) = 1.5789 (A probability distribution greater than 1 is OK. It is the area under the bell curve that is equal to 1. The formula for calculating probability distribution is P(height | male) = (sample height - mean male height) / standard deviation of male height)
P(weight | male) = 5.9881e-06
P(foot size | male) = 1.3112e-3
posterior numerator (male) = their product = 6.1984e-09
P(female) = 0.5
P(height | female) = 2.2346e-1
P(weight | female) = 1.6789e-2
P(foot size | female) = 2.8669e-1
posterior numerator (female) = their product = 5.3778e-04
Since posterior numerator is greater in the female case, we predict the sample is female.
problem.
Consider the problem of classifying documents by their content, for example into spam and non-spam E-mail
s. Imagine that documents are drawn from a number of classes of documents which can be modelled as sets of words where the (independent) probability that the i-th word of a given document occurs in a document from class C can be written as
(For this treatment, we simplify things further by assuming that words are randomly distributed in the document - that is, words are not dependent on the length of the document, position within the document with relation to other words, or other document-context.)
Then the probability that a given document D contains all of the words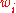
, given a class C, is
The question that we desire to answer is: "what is the probability that a given document D belongs to a given class C?" In other words, what is
?
Now by definition
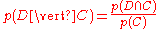
and
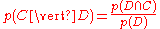
Bayes' theorem manipulates these into a statement of probability in terms of likelihood
.
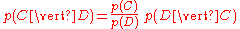
Assume for the moment that there are only two mutually exclusive classes, S and ¬S (e.g. spam and not spam), such that every element (email) is in either one or the other;
and
Using the Bayesian result above, we can write:
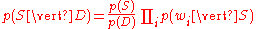
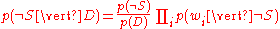
Dividing one by the other gives:
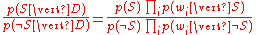
Which can be re-factored as:
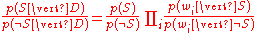
Thus, the probability ratio p(S | D) / p(¬S | D) can be expressed in terms of a series of likelihood ratios.
The actual probability p(S | D) can be easily computed from log (p(S | D) / p(¬S | D)) based on the observation that p(S | D) + p(¬S | D) = 1.
Taking the logarithm
of all these ratios, we have:
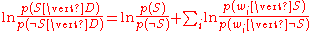
(This technique of "log-likelihood ratios" is a common technique in statistics.
In the case of two mutually exclusive alternatives (such as this example), the conversion of a log-likelihood ratio to a probability takes the form of a sigmoid curve: see logit
for details.)
Finally, the document can be classified as follows. It is spam if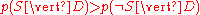
(i.e., 
), otherwise it is not spam.
Software
Publications
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
with strong (naive) independence
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
assumptions. A more descriptive term for the underlying probability model would be "independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
feature model".
In simple terms, a naive Bayes classifier assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or absence) of any other feature, given the class variable. For example, a fruit may be considered to be an apple if it is red, round, and about 4" in diameter. Even if these features depend on each other or upon the existence of the other features, a naive Bayes classifier considers all of these properties to independently contribute to the probability that this fruit is an apple.
Depending on the precise nature of the probability model, naive Bayes classifiers can be trained very efficiently in a supervised learning
Supervised learning
Supervised learning is the machine learning task of inferring a function from supervised training data. The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value...
setting. In many practical applications, parameter estimation for naive Bayes models uses the method of maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
; in other words, one can work with the naive Bayes model without believing in Bayesian probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
or using any Bayesian methods.
In spite of their naive design and apparently over-simplified assumptions, naive Bayes classifiers have worked quite well in many complex real-world situations. In 2004, analysis of the Bayesian classification problem has shown that there are some theoretical reasons for the apparently unreasonable efficacy
Efficacy
Efficacy is the capacity to produce an effect. It has different specific meanings in different fields. In medicine, it is the ability of an intervention or drug to reproduce a desired effect in expert hands and under ideal circumstances.- Healthcare :...
of naive Bayes classifiers. Still, a comprehensive comparison with other classification methods in 2006 showed that Bayes classification is outperformed by more current approaches, such as boosted trees or random forests.
An advantage of the naive Bayes classifier is that it only requires a small amount of training data to estimate the parameters (means and variances of the variables) necessary for classification. Because independent variables are assumed, only the variances of the variables for each class need to be determined and not the entire covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
.
The naive Bayes probabilistic model
Abstractly, the probability model for a classifier is a conditional model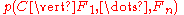over a dependent class variable
with a small number of outcomes or classes, conditional on several feature variables through . The problem is that if the number of features is large or when a feature can take on a large number of values, then basing such a model on probability tables is infeasible. We therefore reformulate the model to make it more tractable.Using Bayes' theorem
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
, we write
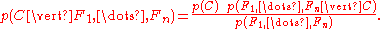
In plain English the above equation can be written as
In practice we are only interested in the numerator of that fraction, since the denominator does not depend on
and the values of the features are given, so that the denominator is effectively constant.The numerator is equivalent to the joint probability model
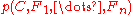
which can be rewritten as follows, using repeated applications of the definition of conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
:
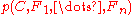
Now the "naive" conditional independence
Conditional independence
In probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
assumptions come into play: assume that each feature
is conditionally independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of every other feature
for . This means that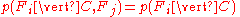for
, and so the joint model can be expressed as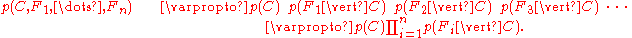This means that under the above independence assumptions, the conditional distribution over the class variable
can be expressed like this: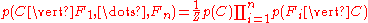where
(the evidence) is a scaling factor dependent only on , i.e., a constant if the values of the feature variables are known.Models of this form are much more manageable, since they factor into a so-called class prior
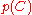and independent probability distributions . If there are 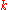classes and if a model for each can be expressed in terms of parameters, then the corresponding naive Bayes model has (k − 1) + n r k parameters. In practice, often (binary classification) and (Bernoulli variables as features) are common, and so the total number of parameters of the naive Bayes model is , where is the number of binary features used for classification and predictionParameter estimation
All model parameters (i.e., class priors and feature probability distributions) can be approximated with relative frequencies from the training set. These are maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimates of the probabilities. A class' prior may be calculated by assuming equiprobable classes (i.e., priors = 1 / (number of classes)), or by calculating an estimate for the class probability from the training set (i.e., (prior for a given class) = (number of samples in the class) / (total number of samples)). To estimate the parameters for a feature's distribution, one must assume a distribution or generate nonparametric models for the features from the training set. If one is dealing with continuous data, a typical assumption is that the continuous values associated with each class are distributed according to a Gaussian distribution.
For example, suppose the training data contains a continuous attribute,
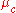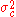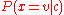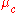. We first segment the data by the class, and then compute the mean and variance of in each class. Let be the mean of the values in associated with class c, and let be the variance of the values in associated with class c. Then, the probability of some value given a class, , can be computed by plugging into the equation for a Normal distribution parameterized by and 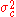. That is,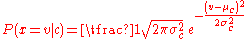Another common technique for handling continuous values is to use binning to discretize
Discretization of continuous features
In statistics and machine learning, discretization refers to the process of converting or partitioning continuous attributes, features or variables to discretized or nominal attributes/features/variables/intervals. This can be useful when creating probability mass functions – formally, in density...
the values. In general, the distribution method is a better choice if there is a small amount of training data, or if the precise distribution of the data is known. The discretization method tends to do better if there is a large amount of training data because it will learn to fit the distribution of the data. Since naive Bayes is typically used when a large amount of data is available (as more computationally expensive models can generally achieve better accuracy), the discretization method is generally preferred over the distribution method.
Sample correction
If a given class and feature value never occur together in the training set then the frequency-based probability estimate will be zero. This is problematic since it will wipe out all information in the other probabilities when they are multiplied. It is therefore often desirable to incorporate a small-sample correction in all probability estimates such that no probability is ever set to be exactly zeroPseudocount
A pseudocount is an amount added to the number of observed cases in order to change the expected probability in a model of those data, when not known to be zero. Depending on the prior knowledge, which is sometimes a subjective value, a pseudocount may have any non-negative finite value...
.
Constructing a classifier from the probability model
The discussion so far has derived the independent feature model, that is, the naive Bayes probability model. The naive Bayes classifierClassifier
Classifier may refer to:*Classifier *Classifier *Classifier *Hierarchical classifier*Linear classifier...
combines this model with a decision rule
Decision rule
In decision theory, a decision rule is a function which maps an observation to an appropriate action. Decision rules play an important role in the theory of statistics and economics, and are closely related to the concept of a strategy in game theory....
. One common rule is to pick the hypothesis that is most probable; this is known as the maximum a posteriori
Maximum a posteriori
In Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
or MAP decision rule. The corresponding classifier is the function
defined as follows: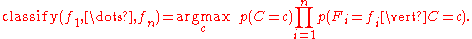Discussion
Despite the fact that the far-reaching independence assumptions are often inaccurate, the naive Bayes classifier has several properties that make it surprisingly useful in practice. In particular, the decoupling of the class conditional feature distributions means that each distribution can be independently estimated as a one dimensional distribution. This in turn helps to alleviate problems stemming from the curse of dimensionalityCurse of dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
, such as the need for data sets that scale exponentially with the number of features. Like all probabilistic classifiers under the MAP decision rule, it arrives at the correct classification as long as the correct class is more probable than any other class; hence class probabilities do not have to be estimated very well. In other words, the overall classifier is robust enough to ignore serious deficiencies in its underlying naive probability model. Other reasons for the observed success of the naive Bayes classifier are discussed in the literature cited below.
Sex classification
Problem: classify whether a given person is a male or a female based on the measured features.The features include height, weight, and foot size.
Training
Example training set below.| sex | height (feet) | weight (lbs) | foot size(inches) |
|---|---|---|---|
| male | 6 | 180 | 12 |
| male | 5.92 (5'11") | 190 | 11 |
| male | 5.58 (5'7") | 170 | 12 |
| male | 5.92 (5'11") | 165 | 10 |
| female | 5 | 100 | 6 |
| female | 5.5 (5'6") | 150 | 8 |
| female | 5.42 (5'5") | 130 | 7 |
| female | 5.75 (5'9") | 150 | 9 |
The classifier created from the training set using a Gaussian distribution assumption would be:
| sex | mean (height) | variance (height) | mean (weight) | variance (weight) | mean (foot size) | variance (foot size) |
|---|---|---|---|---|---|---|
| male | 5.855 | 3.5033e-02 | 176.25 | 1.2292e+02 | 11.25 | 9.1667e-01 |
| female | 5.4175 | 9.7225e-02 | 132.5 | 5.5833e+02 | 7.5 | 1.6667e+00 |
Let's say we have equiprobable classes so P(male)= P(female) = 0.5. There was no identified reason for making this assumption so it may have been a bad idea. If we determine P(C) based on frequency in the training set, we happen to get the same answer.
Testing
Below is a sample to be classified as a male or female.| sex | height (feet) | weight (lbs) | foot size(inches) |
|---|---|---|---|
| sample | 6 | 130 | 8 |
We wish to determine which posterior is greater, male or female. For the classification as male the posterior is given by
For the classification as female the posterior is given by
The evidence (also termed normalizing constant) may be calculated since the sum of the posteriors equals one.
The evidence may be ignored since it is a positive constant. (Normal distributions are always positive.) We now determine the sex of the sample.
P(male) = 0.5
P(height | male) = 1.5789 (A probability distribution greater than 1 is OK. It is the area under the bell curve that is equal to 1. The formula for calculating probability distribution is P(height | male) = (sample height - mean male height) / standard deviation of male height)
P(weight | male) = 5.9881e-06
P(foot size | male) = 1.3112e-3
posterior numerator (male) = their product = 6.1984e-09
P(female) = 0.5
P(height | female) = 2.2346e-1
P(weight | female) = 1.6789e-2
P(foot size | female) = 2.8669e-1
posterior numerator (female) = their product = 5.3778e-04
Since posterior numerator is greater in the female case, we predict the sample is female.
Document Classification
Here is a worked example of naive Bayesian classification to the document classificationDocument classification
Document classification or document categorization is a problem in both library science, information science and computer science. The task is to assign a document to one or more classes or categories. This may be done "manually" or algorithmically...
problem.
Consider the problem of classifying documents by their content, for example into spam and non-spam E-mail
E-mail
Electronic mail, commonly known as email or e-mail, is a method of exchanging digital messages from an author to one or more recipients. Modern email operates across the Internet or other computer networks. Some early email systems required that the author and the recipient both be online at the...
s. Imagine that documents are drawn from a number of classes of documents which can be modelled as sets of words where the (independent) probability that the i-th word of a given document occurs in a document from class C can be written as
(For this treatment, we simplify things further by assuming that words are randomly distributed in the document - that is, words are not dependent on the length of the document, position within the document with relation to other words, or other document-context.)
Then the probability that a given document D contains all of the words
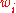, given a class C, isThe question that we desire to answer is: "what is the probability that a given document D belongs to a given class C?" In other words, what is
?Now by definition
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
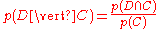
and
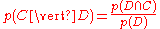
Bayes' theorem manipulates these into a statement of probability in terms of likelihood
Likelihood
Likelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
.
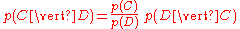
Assume for the moment that there are only two mutually exclusive classes, S and ¬S (e.g. spam and not spam), such that every element (email) is in either one or the other;
and
Using the Bayesian result above, we can write:
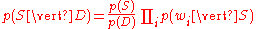
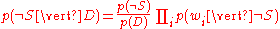
Dividing one by the other gives:
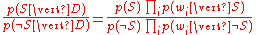
Which can be re-factored as:
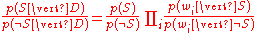
Thus, the probability ratio p(S | D) / p(¬S | D) can be expressed in terms of a series of likelihood ratios.
The actual probability p(S | D) can be easily computed from log (p(S | D) / p(¬S | D)) based on the observation that p(S | D) + p(¬S | D) = 1.
Taking the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of all these ratios, we have:
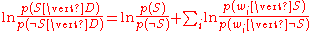
(This technique of "log-likelihood ratios" is a common technique in statistics.
In the case of two mutually exclusive alternatives (such as this example), the conversion of a log-likelihood ratio to a probability takes the form of a sigmoid curve: see logit
Logit
The logit function is the inverse of the sigmoidal "logistic" function used in mathematics, especially in statistics.Log-odds and logit are synonyms.-Definition:The logit of a number p between 0 and 1 is given by the formula:...
for details.)
Finally, the document can be classified as follows. It is spam if
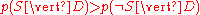(i.e., ), otherwise it is not spam.See also
- AODEAODEAveraged one-dependence estimators is a probabilistic classification learning technique. It was developed to address the attribute-independence problem of the popular naive Bayes classifier...
- Bayesian spam filteringBayesian spam filteringBayesian spam filtering is a statistical technique of e-mail filtering. It makes use of a naive Bayes classifier to identify spam e-mail.Bayesian classifiers work by correlating the use of tokens , with spam and non spam e-mails and then using Bayesian inference to calculate a probability that an...
- Bayesian networkBayesian networkA Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
- Random naive BayesRandom naive BayesRandom naive Bayes extends the Naive Bayes classifier by adopting the random forest principles: random input selection, bagging , and random feature selection .- Naive Bayes classifier :...
- Linear classifierLinear classifierIn the field of machine learning, the goal of statistical classification is to use an object's characteristics to identify which class it belongs to. A linear classifier achieves this by making a classification decision based on the value of a linear combination of the characteristics...
- Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
(esp. as Bayesian techniques relate to spam) - BoostingBoostingBoosting is a machine learning meta-algorithm for performing supervised learning. Boosting is based on the question posed by Kearns: can a set of weak learners create a single strong learner? A weak learner is defined to be a classifier which is only slightly correlated with the true classification...
- Fuzzy logicFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
- Logistic regressionLogistic regressionIn statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
- Class membership probabilitiesClass membership probabilitiesIn general proplems of classification, class membership probabilities reflect the uncertainty with which a given indivual item can be assigned to any given class. Although statistical classification methods by definition generate such probabilities, applications of classification in machine...
- Neural networkNeural networkThe term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
s - Predictive analyticsPredictive analyticsPredictive analytics encompasses a variety of statistical techniques from modeling, machine learning, data mining and game theory that analyze current and historical facts to make predictions about future events....
- PerceptronPerceptronThe perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
- Support vector machineSupport vector machineA support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
External links
- Book Chapter: Naive Bayes text classification, Introduction to Information Retrieval
- Naive Bayes for Text Classification with Unbalanced Classes
- Benchmark results of Naive Bayes implementations
- Hierarchical Naive Bayes Classifiers for uncertain data (an extension of the Naive Bayes classifier).
- winnowTag Create tags that run Bayesian classifiers on over 1/2 million items updated from 7,500 feeds.
- Online application of a Naive Bayes classifier (emotion modelling), with a full explanation.
- dANN: Naive Classifier - Explanation and Example
- BayesNews - Bayesian RSS Reader (useful for personal news clipping).
- Naive Bayes in PMML
- Simple example of document classification with Naive Bayes, implemented in Ruby
- Document Classification Using Naive Bayes Classifier with Perl
Software
- IMSL Numerical LibrariesIMSL Numerical LibrariesIMSL is a commercial collection of software libraries of numerical analysis functionality that are implemented in the computer programming languages of C, Java, C#.NET, and Fortran...
Collections of math and statistical algorithms available in C/C++, Fortran, Java and C#/.NET. Data mining routines in the IMSL Libraries include a Naive Bayes classifier. - OrangeOrange (software)Orange is a component-based data mining and machine learning software suite, featuring friendly yet powerful and flexible visual programming front-end for explorative data analysis and visualization, and Python bindings and libraries for scripting...
, a free data mining software suite, module orngBayes - Winnow content recommendation Open source Naive Bayes text classifier works with very small training and unbalanced training sets. High performance, C, any Unix.
- Naive Bayes implementation in Visual Basic (includes executable and source code).
- An interactive Microsoft ExcelMicrosoft ExcelMicrosoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
spreadsheet Naive Bayes implementation using VBAVisual Basic for ApplicationsVisual Basic for Applications is an implementation of Microsoft's event-driven programming language Visual Basic 6 and its associated integrated development environment , which are built into most Microsoft Office applications...
(requires enabled macros) with viewable source code. - jBNC - Bayesian Network Classifier Toolbox
- POPFile Perl-based email proxy system classifies email into user-defined "buckets", including spam.
- Statistical Pattern Recognition Toolbox for Matlab.
- sux0r An Open SourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
Content management systemContent management systemA content management system is a system providing a collection of procedures used to manage work flow in a collaborative environment. These procedures can be manual or computer-based...
with a focus on Naive Bayesian categorization and probabilistic content. - ifile - the first freely available (Naive) Bayesian mail/spam filter
- NClassifier - NClassifier is a .NET library that supports text classification and text summarization. It is a port of the Nick Lothian's popular Java text classification engine, Classifier4J.
- Classifier4J - Classifier4J is a Java library designed to do text classification. It comes with an implementation of a Bayesian classifier, and now has some other features, including a text summary facility.
- MALLET - A Java package for document classification and other natural language processing tasks.
- nBayes - nBayes is an open source .NET library written in C#
- Apache Mahout - Machine learning package offered by Apache Open Source
- Weka - Popular open source machine learning package, written in Java
- C# implementation of Naive Bayes used for documents categorization that includes files processing, stop words filtering and stemming. Same site offers comparison to other algorithms.
Publications
- Domingos, Pedro & Michael Pazzani (1997) "On the optimality of the simple Bayesian classifier under zero-one loss". Machine Learning, 29:103–137. (also online at CiteSeer: http://citeseer.ist.psu.edu/domingos97optimality.html)
- Rish, Irina. (2001). "An empirical study of the naive Bayes classifier". IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence. (available online: PDF, PostScript)
- Hand, DJ, & Yu, K. (2001). "Idiot's Bayes - not so stupid after all?" International Statistical Review. Vol 69 part 3, pages 385-399. ISSN 0306-7734.
- Webb, G. I., J. Boughton, and Z. Wang (2005). Not So Naive Bayes: Aggregating One-Dependence Estimators. Machine Learning 58(1). Netherlands: Springer, pages 5-24.
- Mozina M, Demsar J, Kattan M, & Zupan B. (2004). "Nomograms for Visualization of Naive Bayesian Classifier". In Proc. of PKDD-2004, pages 337-348. (available online: PDF)
- Maron, M. E. (1961). "Automatic Indexing: An Experimental Inquiry." Journal of the ACM (JACM) 8(3):404–417. (available online: PDF)
- Minsky, M. (1961). "Steps toward Artificial Intelligence." Proceedings of the IRE 49(1):8-30.
- McCallum, A. and Nigam K. "A Comparison of Event Models for Naive Bayes Text Classification". In AAAI/ICML-98 Workshop on Learning for Text Categorization, pp. 41–48. Technical Report WS-98-05. AAAI Press. 1998. (available online: PDF)
- Rennie J, Shih L, Teevan J, and Karger D. Tackling The Poor Assumptions of Naive Bayes Classifiers. In Proceedings of the Twentieth International Conference on Machine Learning (ICML). 2003. (available online: PDF)