Gibbs sampling
Encyclopedia
In statistics
and in statistical physics
, Gibbs sampling or a Gibbs sampler is an algorithm
to generate a sequence of samples from the joint probability distribution of two or more random variable
s. The purpose of such a sequence is to approximate the joint distribution; to approximate the marginal distribution
of one of the variables, or some subset of the variables (for example, the unknown parameter
s or latent variable
s); or to compute an integral
(such as the expected value
of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference
, especially Bayesian inference
. It is a randomized algorithm
(i.e. an algorithm that makes use of random number
s, and hence produces different results each time it is run), and is an alternative to deterministic algorithm
s for statistical inference such as variational Bayes
or the expectation-maximization algorithm
(EM).
Gibbs sampling is an example of a Markov chain Monte Carlo
algorithm. The algorithm is named after the physicist J. W. Gibbs, in reference to an analogy between the sampling
algorithm and statistical physics
. The algorithm was described by brothers Stuart and Donald Geman
in 1984, some eight decades after the passing of Gibbs.
In its basic version, Gibbs sampling is a special case of the Metropolis–Hastings algorithm. However, in its extended versions (see below), it can be considered a general framework for sampling from a large set of variables by sampling each variable (or in some cases, each group of variables) in turn, and can incorporate the Metropolis–Hastings algorithm (or similar methods such as slice sampling
) to implement one or more of the sampling steps.
Gibbs sampling is applicable when the joint distribution is not known explicitly or is difficult to sample from directly, but the conditional distribution
of each variable is known and is easy (or at least, easier) to sample from. The Gibbs sampling algorithm generates an instance from the distribution of each variable in turn, conditional on the current values of the other variables. It can be shown (see, for example, Gelman et al. 1995) that the sequence of samples constitutes a Markov chain
, and the stationary distribution of that Markov chain is just the sought-after joint distribution.
Gibbs sampling is particularly well-adapted to sampling the posterior distribution
of a Bayesian network
, since Bayesian networks are typically specified as a collection of conditional distributions.
by integrating over a joint distribution
. Suppose we want to obtain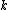
samples of 
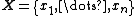from a joint distribution 
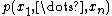. Denote the 
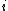th sample by 
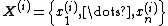. We proceed as follows:
The samples then approximate the joint distribution of all variables. Furthermore, the marginal distribution of any subset of variables can be approximated by simply examining the samples for that subset of variables, ignoring the rest. In addition, the expected value
of any variable can be approximated by averaging over all the samples.
Observed data is incorporated into the sampling process by creating separate variables for each piece of observed data and fixing the variables in question to their observed values, rather than sampling from those variables. Supervised learning
can be done using a similar process. It is also easy to incorporate data with missing values, or to do semi-supervised learning
, by simply fixing the values of all variables whose values are known, and sampling from the remainder.
For observed data, there will be one variable for each observation — rather than, for example, one variable corresponding to the sample mean or sample variance of a set of observations. In fact, there generally will be no variables at all corresponding to concepts such as "sample mean" or "sample variance". Instead, in such a case there will be variables representing the unknown true mean and true variance, and the determination of sample values for these variables results automatically from the operation of the Gibbs sampler.
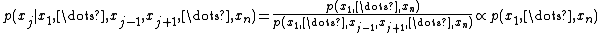
"Proportional to" in this case means that the denominator is not a function of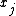
and thus is the same for all values of 
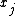; it forms part of the normalization constant for the distribution over 
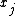. In practice, to determine the nature of the conditional distribution of a factor 
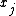, it is easiest to factor the joint distribution according to the individual conditional distributions defined by the graphical model
over the variables, ignore all factors that are not functions of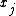
(all of which, together with the denominator above, constitute the normalization constant), and then reinstate the normalization constant at the end, as necessary. In practice, this means doing one of three things:
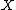is taken from a distribution depending on a parameter vector 
of length 
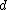, with prior distribution 
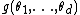. It may be that 
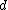is very large and that numerical integration to find the marginal densities of the 
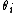would be computationally expensive. Then an alternative method of calculating the marginal densities is to create a Markov chain on the space 
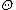by repeating these two steps:
These steps define a reversible Markov chain
with the desired invariant distribution
. This
can be proved as follows. Define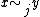
if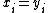 
for all 
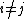and let 
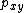denote the probability of a jump from 
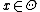to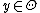 
. Then, the transition probabilities are
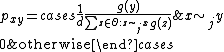
So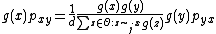
since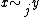
is an equivalence relation
. Thus the detailed balance equations are satisfied, implying the chain is reversible and it has invariant distribution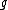
.
In practice, the suffix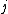
is not chosen at random, and the chain cycles through the suffixes in order. In general this gives a non-stationary Markov process, but each individual step will still be reversible, and the overall process will still have the desired stationary distribution (as long as the chain can access all states under the fixed ordering).
The primary purpose of these variations is to reduce autocorrelation
between samples (see above). Depending on the particular conditional distributions and the nature of the observed data, this may or may not help. Commonly, blocked or collapsed Gibbs sampling increases the complexity of the sampling process because it induces greater dependencies among variables, but in some cases, it may actually make things easier.
It is also possible to extend Gibbs sampling in various ways. For example, in the case of variables whose conditional distribution is not easy to sample from, a single iteration of slice sampling
or the Metropolis-Hastings algorithm
can be used to sample from the variables in question. It is also possible to incorporate variables that are not random variables, but whose value is deterministically computed from other variables. Generalized linear models, e.g. logistic regression
(aka "maximum entropy models"), can be incorporated in this fashion. (BUGS, for example, allows this type of mixing of models.)
The second problem can happen even when all states have nonzero probability and there is only a single island of high-probability states. For example, consider a probability distribution over 100-bit vectors, where the all-zeros vector occurs with probability ½, and all other vectors are equally probable, and so have a probability of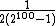
each. If you want to estimate the probability of the zero vector, it would be sufficient to take 100 or 1000 samples from the true distribution. That would very likely give an answer very close to ½. But you would probably have to take more than 
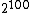samples from Gibbs sampling to get the same result. No computer could do this in a lifetime.
This problem occurs no matter how long the burn in period is. This is because in the true distribution, the zero vector occurs half the time, and those occurrences are randomly mixed in with the nonzero vectors. Even a small sample will see both zero and nonzero vectors. But Gibbs sampling will alternate between returning only the zero vector for long periods (about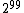
in a row), then only nonzero vectors for long periods (about 
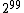in a row). Thus convergence to the true distribution is extremely slow, requiring much more than 
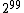steps; taking this many steps is not computationally feasible in a reasonable time period. The slow convergence here can be seen as a consequence of the curse of dimensionality
.
Note that a problem like this can be solved by block sampling the entire 100-bit vector at once. (This assumes that the 100-bit vector is part of a larger set of variables. If this vector is the only thing being sampled, then block sampling is equivalent to not doing Gibbs sampling at all, which by hypothesis would be difficult.)
software (Bayesian inference Using Gibbs Sampling; the open source
version is called OpenBUGS
) does a Bayesian analysis of complex statistical models using Markov chain Monte Carlo
.
JAGS
(Just another Gibbs sampler) is a GPL program for analysis of Bayesian hierarchical models using Markov Chain Monte Carlo.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and in statistical physics
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
, Gibbs sampling or a Gibbs sampler is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to generate a sequence of samples from the joint probability distribution of two or more random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. The purpose of such a sequence is to approximate the joint distribution; to approximate the marginal distribution
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
of one of the variables, or some subset of the variables (for example, the unknown parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s or latent variable
Latent variable
In statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
s); or to compute an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
(such as the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
, especially Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
. It is a randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
(i.e. an algorithm that makes use of random number
Random number
Random number may refer to:* A number generated for or part of a set exhibiting statistical randomness.* A random sequence obtained from a stochastic process.* An algorithmically random sequence in algorithmic information theory....
s, and hence produces different results each time it is run), and is an alternative to deterministic algorithm
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
s for statistical inference such as variational Bayes
Variational Bayes
Variational Bayesian methods, also called ensemble learning, are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning...
or the expectation-maximization algorithm
Expectation-maximization algorithm
In statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
(EM).
Gibbs sampling is an example of a Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
algorithm. The algorithm is named after the physicist J. W. Gibbs, in reference to an analogy between the sampling
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
algorithm and statistical physics
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
. The algorithm was described by brothers Stuart and Donald Geman
Donald Geman
Donald Geman is an American statistician and a leading researcher in the realm of machine learning and pattern recognition...
in 1984, some eight decades after the passing of Gibbs.
In its basic version, Gibbs sampling is a special case of the Metropolis–Hastings algorithm. However, in its extended versions (see below), it can be considered a general framework for sampling from a large set of variables by sampling each variable (or in some cases, each group of variables) in turn, and can incorporate the Metropolis–Hastings algorithm (or similar methods such as slice sampling
Slice sampling
Slice sampling is a type of Markov chain Monte Carlo algorithm for pseudo-random number sampling, i.e. for drawing random samples from a statistical distribution...
) to implement one or more of the sampling steps.
Gibbs sampling is applicable when the joint distribution is not known explicitly or is difficult to sample from directly, but the conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
of each variable is known and is easy (or at least, easier) to sample from. The Gibbs sampling algorithm generates an instance from the distribution of each variable in turn, conditional on the current values of the other variables. It can be shown (see, for example, Gelman et al. 1995) that the sequence of samples constitutes a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
, and the stationary distribution of that Markov chain is just the sought-after joint distribution.
Gibbs sampling is particularly well-adapted to sampling the posterior distribution
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
of a Bayesian network
Bayesian network
A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
, since Bayesian networks are typically specified as a collection of conditional distributions.
Implementation
Gibbs sampling, in its basic incarnation, is a special case of the Metropolis–Hastings algorithm. The point of Gibbs sampling is that given a multivariate distribution it is simpler to sample from a conditional distribution than to marginalizeConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
by integrating over a joint distribution
Joint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
. Suppose we want to obtain
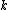samples of 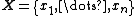from a joint distribution 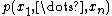. Denote the 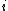th sample by 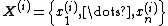. We proceed as follows:- We begin with some initial value
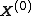for each variable. - For each sample
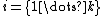, sample each variable 
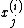from the conditional distribution 
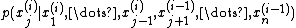. That is, sample each variable from the distribution of that variable conditioned on all other variables, making use of the most recent values and updating the variable with its new value as soon as it has been sampled.
The samples then approximate the joint distribution of all variables. Furthermore, the marginal distribution of any subset of variables can be approximated by simply examining the samples for that subset of variables, ignoring the rest. In addition, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of any variable can be approximated by averaging over all the samples.
Observed data is incorporated into the sampling process by creating separate variables for each piece of observed data and fixing the variables in question to their observed values, rather than sampling from those variables. Supervised learning
Supervised learning
Supervised learning is the machine learning task of inferring a function from supervised training data. The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value...
can be done using a similar process. It is also easy to incorporate data with missing values, or to do semi-supervised learning
Semi-supervised learning
In computer science, semi-supervised learning is a class of machine learning techniques that make use of both labeled and unlabeled data for training - typically a small amount of labeled data with a large amount of unlabeled data...
, by simply fixing the values of all variables whose values are known, and sampling from the remainder.
For observed data, there will be one variable for each observation — rather than, for example, one variable corresponding to the sample mean or sample variance of a set of observations. In fact, there generally will be no variables at all corresponding to concepts such as "sample mean" or "sample variance". Instead, in such a case there will be variables representing the unknown true mean and true variance, and the determination of sample values for these variables results automatically from the operation of the Gibbs sampler.
- The initial values of the variables can be determined randomly or by some other algorithm such as expectation-maximization.
- It is not actually necessary to determine an initial value for the first variable sampled.
- It is common to ignore some number of samples at the beginning (the so-called burn-in period), and then consider only every
th sample when averaging values to compute an expectation. For example, the first 1,000 samples might be ignored, and then every 100th sample averaged, throwing away all the rest. The reason for this is that (1) successive samples are not independent of each other but form a Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
with some amount of correlation; (2) the stationary distributionStationary distributionStationary distribution may refer to:* The limiting distribution in a Markov chain* The marginal distribution of a stationary process or stationary time series* The set of joint probability distributions of a stationary process or stationary time series...
of the Markov chain is the desired joint distribution over the variables, but it may take awhile for that stationary distribution to be reached. Sometimes, algorithms can be used to determine the amount of autocorrelationAutocorrelationAutocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
between samples and the value of
(the period between samples that are actually used) computed from this, but in practice there is a fair amount of "black magic" involved. - The process of simulated annealingSimulated annealingSimulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
is often used to reduce the "random walkRandom walkA random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
" behavior in the early part of the sampling process (i.e. the tendency to move slowly around the sample space, with a high amount of autocorrelationAutocorrelationAutocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
between samples, rather than moving around quickly, as is desired). Other techniques that may reduce autocorrelation are collapsed Gibbs sampling, blocked Gibbs sampling, and ordered overrelaxation; see below.
Relation of conditional distribution and joint distribution
Furthermore, the conditional distribution of one variable given all others is proportional to the joint distribution: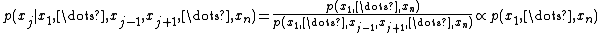"Proportional to" in this case means that the denominator is not a function of
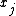and thus is the same for all values of 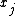; it forms part of the normalization constant for the distribution over 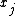. In practice, to determine the nature of the conditional distribution of a factor 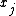, it is easiest to factor the joint distribution according to the individual conditional distributions defined by the graphical modelGraphical model
A graphical model is a probabilistic model for which a graph denotes the conditional independence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning....
over the variables, ignore all factors that are not functions of
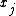(all of which, together with the denominator above, constitute the normalization constant), and then reinstate the normalization constant at the end, as necessary. In practice, this means doing one of three things:
- If the distribution is discrete, the individual probabilities of all possible values of
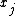are computed, and then summed to find the normalization constant. - If the distribution is continuous and of a known form, the normalization constant will also be known.
- In other cases, the normalization constant can usually be ignored, as most sampling methods do not require it.
Mathematical background
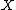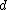Suppose that a sample is taken from a distribution depending on a parameter vector of length , with prior distribution 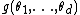. It may be that 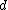is very large and that numerical integration to find the marginal densities of the 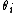would be computationally expensive. Then an alternative method of calculating the marginal densities is to create a Markov chain on the space by repeating these two steps:- Pick a random index
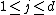
- Pick a new value for
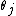according to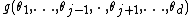 
These steps define a reversible Markov chain
Detailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
with the desired invariant distribution
. Thiscan be proved as follows. Define
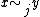if 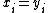for all 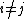and let 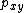denote the probability of a jump from 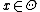to 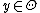. Then, the transition probabilities are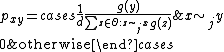So
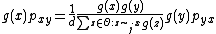
since
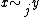is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
. Thus the detailed balance equations are satisfied, implying the chain is reversible and it has invariant distribution
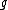.In practice, the suffix
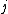is not chosen at random, and the chain cycles through the suffixes in order. In general this gives a non-stationary Markov process, but each individual step will still be reversible, and the overall process will still have the desired stationary distribution (as long as the chain can access all states under the fixed ordering).Variations and extensions
- A blocked Gibbs sampler groups two or more variables together and samples from their joint distributionJoint distributionIn the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
conditioned on all other variables, rather than sampling from each one individually. For example, in a hidden Markov modelHidden Markov modelA hidden Markov model is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E...
, a blocked Gibbs sampler might sample from all the latent variableLatent variableIn statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
s making up the Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
in one go, using the forward-backward algorithm. - A collapsed Gibbs sampler integrates out (marginalizes overMarginal distributionIn probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
) one or more variables when sampling for some other variable. For example, imagine that a model consists of three variables A, B, and C. A simple Gibbs sampler would sample from p(A|B,C), then p(B|A,C), then p(C|A,B). A collapsed Gibbs sampler might replace the sampling step for A with a sample taken from the marginal distribution p(A|C), with variable B integrated out in this case. Alternatively, variable B could be collapsed out entirely, alternately sampling from p(A|C) and p(C|A) and not sampling over B at all. The distribution over a variable A that arises when collapsing a parent variable B is called a compound distribution; sampling from this distribution is generally tractable when B is the conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
for A, particularly when A and B are members of the exponential familyExponential familyIn probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
. For more information, see the article on compound distributions or Liu (1994). - A Gibbs sampler with ordered overrelaxation samples a given odd number of candidate values for
at any given step and sorts them, along with the single value for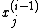 
according to some well-defined ordering. If 
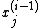is the sth smallest in the sorted list then the 
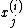is selected as the sth largest in the sorted list. For more information, see Neal (1995).
The primary purpose of these variations is to reduce autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
between samples (see above). Depending on the particular conditional distributions and the nature of the observed data, this may or may not help. Commonly, blocked or collapsed Gibbs sampling increases the complexity of the sampling process because it induces greater dependencies among variables, but in some cases, it may actually make things easier.
It is also possible to extend Gibbs sampling in various ways. For example, in the case of variables whose conditional distribution is not easy to sample from, a single iteration of slice sampling
Slice sampling
Slice sampling is a type of Markov chain Monte Carlo algorithm for pseudo-random number sampling, i.e. for drawing random samples from a statistical distribution...
or the Metropolis-Hastings algorithm
Metropolis-Hastings algorithm
In mathematics and physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo method for obtaining a sequence of random samples from a probability distribution for which direct sampling is difficult...
can be used to sample from the variables in question. It is also possible to incorporate variables that are not random variables, but whose value is deterministically computed from other variables. Generalized linear models, e.g. logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
(aka "maximum entropy models"), can be incorporated in this fashion. (BUGS, for example, allows this type of mixing of models.)
Failure modes
There are two ways that Gibbs sampling can fail. The first is when there are islands of high-probability states, with no paths between them. For example, consider a probability distribution over 2-bit vectors, where the vectors (0,0) and (1,1) each have probability ½, but the other two vectors (0,1) and (1,0) have probability zero. Gibbs sampling will become trapped in one of the two high-probability vectors, and will never reach the other one. More generally, for any distribution over high-dimensional, real-valued vectors, if two particular elements of the vector are perfectly correlated (or perfectly anti-correlated), those two elements will become stuck, and Gibbs sampling will never be able to change them.The second problem can happen even when all states have nonzero probability and there is only a single island of high-probability states. For example, consider a probability distribution over 100-bit vectors, where the all-zeros vector occurs with probability ½, and all other vectors are equally probable, and so have a probability of
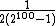each. If you want to estimate the probability of the zero vector, it would be sufficient to take 100 or 1000 samples from the true distribution. That would very likely give an answer very close to ½. But you would probably have to take more than 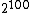samples from Gibbs sampling to get the same result. No computer could do this in a lifetime.This problem occurs no matter how long the burn in period is. This is because in the true distribution, the zero vector occurs half the time, and those occurrences are randomly mixed in with the nonzero vectors. Even a small sample will see both zero and nonzero vectors. But Gibbs sampling will alternate between returning only the zero vector for long periods (about
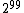in a row), then only nonzero vectors for long periods (about 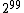in a row). Thus convergence to the true distribution is extremely slow, requiring much more than 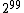steps; taking this many steps is not computationally feasible in a reasonable time period. The slow convergence here can be seen as a consequence of the curse of dimensionalityCurse of dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
.
Note that a problem like this can be solved by block sampling the entire 100-bit vector at once. (This assumes that the 100-bit vector is part of a larger set of variables. If this vector is the only thing being sampled, then block sampling is equivalent to not doing Gibbs sampling at all, which by hypothesis would be difficult.)
Software
The WinBUGSWinBUGS
WinBUGS is statistical software for Bayesian analysis using Markov chain Monte Carlo methods.It is based on the BUGS project started in 1989...
software (Bayesian inference Using Gibbs Sampling; the open source
Open source
The term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
version is called OpenBUGS
OpenBUGS
OpenBUGS is a computer software for the Bayesian analysis of complex statistical models using Markov chain Monte Carlo methods. OpenBUGS is the open source variant of WinBUGS . It runs under Windows and Linux, as well as from inside the R statistical package...
) does a Bayesian analysis of complex statistical models using Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
.
JAGS
Just another Gibbs sampler
Just another Gibbs sampler is a program for analysis of Bayesian hierarchical models using Markov chain Monte Carlo developed by Martyn Plummer...
(Just another Gibbs sampler) is a GPL program for analysis of Bayesian hierarchical models using Markov Chain Monte Carlo.
External links
- The BUGS Project - Bayesian inference Using Gibbs Sampling
- A simple explanation of Gibbs sampling can be found on pp. 370–371 of Prof. MacKay's book "Information Theory, Inference, and Learning Algorithms", available for free browsing here or here.
- A practical application of Gibbs sampling in genomics.