
Variational Bayes
Encyclopedia
Variational Bayesian methods, also called 'ensemble learning', are a family of techniques for approximating intractable integral
s arising in Bayesian inference
and machine learning
. They are typically used in complex statistical model
s consisting of observed variables (usually termed "data") as well as unknown parameter
s and latent variable
s, with various sorts of relationships among the three types of random variable
s, as might be described by a graphical model
. As is typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods can provide an analytical approximation to the posterior probability
of the unobserved variables, and also to derive a lower bound for the marginal likelihood
(sometimes called the "evidence") of several models (i.e. the marginal probability of the data given the model, with marginalization performed over unobserved variables), with a view to performing model selection
. It is an alternative to Monte Carlo sampling methods for taking a fully Bayesian approach to statistical inference
over complex distributions
that are difficult to directly evaluate or sample
from.
Variational Bayes can be seen as an extension of the EM (expectation-maximization) algorithm from maximum a posteriori estimation (MAP estimation) of the single most probable value of each parameter to fully Bayesian estimation which computes(an approximation to) the entire posterior distribution of the parameters and latent variables.
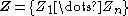 given some data
given some data 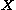 is approximated
is approximated
by a variational distribution,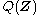 :
: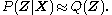
The distribution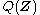 is restricted to belong to a family of distributions of simpler
is restricted to belong to a family of distributions of simpler
form than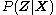 , selected with the intention of making
, selected with the intention of making 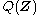 similar to the true posterior,
similar to the true posterior, 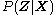 . The lack of similarity is measured in terms of
. The lack of similarity is measured in terms of
a dissimilarity function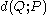 and hence inference is performed by selecting the distribution
and hence inference is performed by selecting the distribution
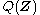 that minimizes
that minimizes 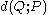 . One choice of dissimilarity function that makes this minimization tractable is the Kullback–Leibler divergence
. One choice of dissimilarity function that makes this minimization tractable is the Kullback–Leibler divergence
(KL divergence) of P from Q, defined as
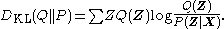
This can be written as
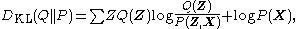
or
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s arising in Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
and machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
. They are typically used in complex statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
s consisting of observed variables (usually termed "data") as well as unknown parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s and latent variable
Latent variable
In statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
s, with various sorts of relationships among the three types of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, as might be described by a graphical model
Graphical model
A graphical model is a probabilistic model for which a graph denotes the conditional independence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning....
. As is typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods can provide an analytical approximation to the posterior probability
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
of the unobserved variables, and also to derive a lower bound for the marginal likelihood
Marginal likelihood
In statistics, a marginal likelihood function, or integrated likelihood, is a likelihood function in which some parameter variables have been marginalised...
(sometimes called the "evidence") of several models (i.e. the marginal probability of the data given the model, with marginalization performed over unobserved variables), with a view to performing model selection
Model selection
Model selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
. It is an alternative to Monte Carlo sampling methods for taking a fully Bayesian approach to statistical inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
over complex distributions
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
that are difficult to directly evaluate or sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
from.
Variational Bayes can be seen as an extension of the EM (expectation-maximization) algorithm from maximum a posteriori estimation (MAP estimation) of the single most probable value of each parameter to fully Bayesian estimation which computes(an approximation to) the entire posterior distribution of the parameters and latent variables.
Mathematical derivation
In variational inference, the posterior distribution over a set of unobserved variables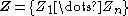 given some data
given some data 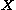 is approximated
is approximatedby a variational distribution,
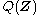 :
: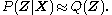
The distribution
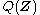 is restricted to belong to a family of distributions of simpler
is restricted to belong to a family of distributions of simplerform than
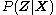 , selected with the intention of making
, selected with the intention of making 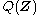 similar to the true posterior,
similar to the true posterior, 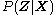 . The lack of similarity is measured in terms of
. The lack of similarity is measured in terms ofa dissimilarity function
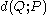 and hence inference is performed by selecting the distribution
and hence inference is performed by selecting the distribution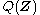 that minimizes
that minimizes 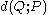 . One choice of dissimilarity function that makes this minimization tractable is the Kullback–Leibler divergence
. One choice of dissimilarity function that makes this minimization tractable is the Kullback–Leibler divergenceKullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
(KL divergence) of P from Q, defined as
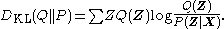
This can be written as
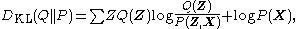
or
-
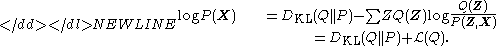
As the so-called log evidence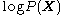 is fixed with respect to
is fixed with respect to 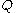 , maximising the final term
, maximising the final term 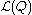 minimizes the KL divergence of
minimizes the KL divergence of 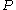 from
from 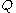 . By appropriate choice of
. By appropriate choice of 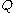 ,
, 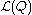 becomes tractable to compute and to maximize. Hence we have both an analytical approximation
becomes tractable to compute and to maximize. Hence we have both an analytical approximation 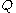 for the posterior
for the posterior 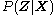 , and a lower bound
, and a lower bound 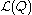 for the evidence
for the evidence 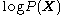 . The lower bound
. The lower bound 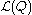 is known as the (negative) variational free energyThermodynamic free energyThe thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
is known as the (negative) variational free energyThermodynamic free energyThe thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
because it can also be expressed as an "energy"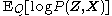 plus the entropy of
plus the entropy of 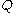 .
.
In practice
The variational distribution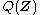 is usually assumed to factorize over some partitionPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
is usually assumed to factorize over some partitionPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the latent variables, i.e. for some partition of the latent variables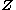 into
into 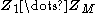 ,
,
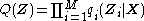
It can be shown using the calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
(hence the name "variational Bayes") that the "best" distribution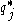 for each of the factors
for each of the factors 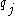 (in terms of the distribution minimizing the KL divergence, as described above) can be expressed as:
(in terms of the distribution minimizing the KL divergence, as described above) can be expressed as:
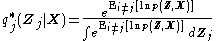
where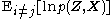 is the expectationExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
is the expectationExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the joint probability of the data and latent variables, taken over all variables not in the partition.
In practice, we usually work in terms of logarithms, i.e.:
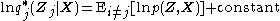
The constant in the above expression is related to the normalizing constantNormalizing constantThe concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
(the denominator in the expression above for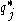 ) and is usually reinstated by inspection, as the rest of the expression can usually be recognized as being a known type of distribution (e.g. Gaussian, gamma, etc.).
) and is usually reinstated by inspection, as the rest of the expression can usually be recognized as being a known type of distribution (e.g. Gaussian, gamma, etc.).
Using the properties of expectations, the expression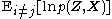 can usually be simplified into a function of the fixed hyperparameterHyperparameterIn Bayesian statistics, a hyperparameter is a parameter of a prior distribution; the term is used to distinguish them from parameters of the model for the underlying system under analysis...
can usually be simplified into a function of the fixed hyperparameterHyperparameterIn Bayesian statistics, a hyperparameter is a parameter of a prior distribution; the term is used to distinguish them from parameters of the model for the underlying system under analysis...
s of the prior distributions over the latent variables and of expectations (and sometimes higher momentMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
s such as the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
) of latent variables not in the current partition (i.e. latent variables not included in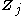 ). This creates circular dependencies between the parameters of the distributions over variables in one partition and the expectations of variables in the other partitions. This naturally suggests an iterative algorithm, much like EM (the expectation-maximization algorithm), in which the expectations (and possibly higher moments) of the latent variables are initialized in some fashion (perhaps randomly), and then the parameters of each distribution are computed in turn using the current values of the expectations, after which the expectation of the newly computed distribution is set appropriately according to the computed parameters. An algorithm of this sort is guaranteed to convergeLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
). This creates circular dependencies between the parameters of the distributions over variables in one partition and the expectations of variables in the other partitions. This naturally suggests an iterative algorithm, much like EM (the expectation-maximization algorithm), in which the expectations (and possibly higher moments) of the latent variables are initialized in some fashion (perhaps randomly), and then the parameters of each distribution are computed in turn using the current values of the expectations, after which the expectation of the newly computed distribution is set appropriately according to the computed parameters. An algorithm of this sort is guaranteed to convergeLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
. Furthermore, if the distributions in question are part of the exponential familyExponential familyIn probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
, which is usually the case, convergence will be to a global maximum, since the exponential family is convexConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
.
In other words, for each of the partitions of variables, by simplifying the expression for the distribution over the partition's variables and examining the distribution's functional dependency on the variables in question, the family of the distribution can usually be determined (which in turn determines the value of the constant). The formula for the distribution's parameters will be expressed in terms of the prior distributions' hyperparameters (which are known constants), but also in terms of expectations of functions of variables in other partitions. Usually these expectations can be simplified into functions of expectations of the variables themselves (i.e. the meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
s); sometimes expectations of squared variables (which can be related to the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the variables), or expectations of higher powers (i.e. higher momentMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
s) also appear. In most cases, the other variables' distributions will be from known families, and the formulas for the relevant expectations can be looked up. However, those formulas depend on those distributions' parameters, which depend in turn on the expectations about other variables. The result is that the formulas for the parameters of each variable's distributions can be expressed as a series of equations with mutual, nonlinear dependencies among the variables. Usually, it is not possible to solve this system of equations directly. However, as described above, the dependencies suggest a simple iterative algorithm, which in most cases is guaranteed to converge. An example will make this process clearer.
A simple example
Imagine a simple Bayesian model consisting of a single node with a Gaussian distribution, with unknown meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and precisionPrecision (statistics)In statistics, the term precision can mean a quantity defined in a specific way. This is in addition to its more general meaning in the contexts of accuracy and precision and of precision and recall....
(or equivalently, an unknown varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, since the precision is the reciprocal of the variance).
We place conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
distributions on the unknown mean and variance, i.e. the mean also follows a Gaussian distribution while the precision follows a gamma distribution. In other words:
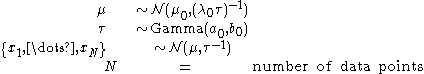
We are given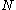 data points
data points 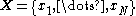 and our goal is to infer the posterior distribution
and our goal is to infer the posterior distribution 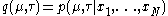 of the parameters
of the parameters 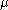 and
and  .
.
The hyperparameterHyperparameterIn Bayesian statistics, a hyperparameter is a parameter of a prior distribution; the term is used to distinguish them from parameters of the model for the underlying system under analysis...
s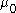 ,
, 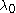 ,
, 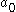 and
and 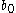 are fixed, given values. They can be set to small positive numbers to give broad prior distributions indicating ignorance about the prior distributions of
are fixed, given values. They can be set to small positive numbers to give broad prior distributions indicating ignorance about the prior distributions of 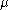 and
and  .
.
The joint probability of all variables can be rewritten as
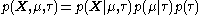
where the individual factors are
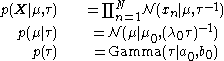
where
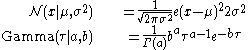
Assume that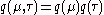 , i.e. that the posterior distribution factorizes into independent factors for
, i.e. that the posterior distribution factorizes into independent factors for 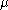 and
and  . This type of assumption underlies the variational Bayesian method. The true posterior distribution does not in fact factor this way (in fact, in this simple case, it is known to be a Gaussian-gamma distribution), and hence the result we obtain will be an approximation.
. This type of assumption underlies the variational Bayesian method. The true posterior distribution does not in fact factor this way (in fact, in this simple case, it is known to be a Gaussian-gamma distribution), and hence the result we obtain will be an approximation.
Then
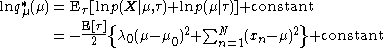
Note that the term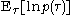 will be a function solely of
will be a function solely of 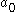 and
and 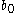 and hence is constant with respect to
and hence is constant with respect to 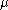 ; thus it has been absorbed into the constant term at the end. By expanding the squares inside of the braces, separating out and grouping the terms involving
; thus it has been absorbed into the constant term at the end. By expanding the squares inside of the braces, separating out and grouping the terms involving 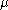 and
and 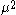 and completing the squareCompleting the squareIn elementary algebra, completing the square is a technique for converting a quadratic polynomial of the formax^2 + bx + c\,\!to the formIn this context, "constant" means not depending on x. The expression inside the parenthesis is of the form ...
and completing the squareCompleting the squareIn elementary algebra, completing the square is a technique for converting a quadratic polynomial of the formax^2 + bx + c\,\!to the formIn this context, "constant" means not depending on x. The expression inside the parenthesis is of the form ...
over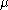 , we see that
, we see that 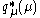 is a Gaussian distribution
is a Gaussian distribution 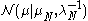 where we have defined:
where we have defined:
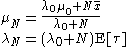
Similarly,
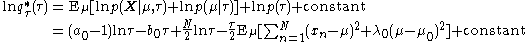
Exponentiating both sides, we can see that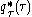 is a gamma distribution
is a gamma distribution 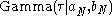 where we have defined
where we have defined
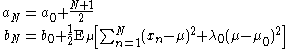
In each case, the parameters for the distribution over one of the variables depend on expectations taken with respect to the other variable. The formulas for the expectations of moments of the Gaussian and gamma distributions are well-known, but depend on the parameters. Hence the formulas for each distribution's parameters depend on the other distribution's parameters. This naturally suggests an EMExpectation-maximization algorithmIn statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
-like algorithm where we first initialize the parameters to some values (perhaps the values of the hyperparameters of the corresponding prior distributions) and iterate, computing new values for each set of parameters using the current values of the other parameters. This is guaranteed to converge to a local maximum, and since both posterior distributions are in the exponential familyExponential familyIn probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
, this local maximum will be a global maximum.
Note also that the posterior distributions have the same form as the corresponding prior distributions. We did not assume this; the only assumption we made was that the distributions factorize, and the form of the distributions followed naturally. It turns out (see below) that the fact that the posterior distributions have the same form as the prior distributions is not a coincidence, but a general result whenever the prior distributions are members of the exponential familyExponential familyIn probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
, which is the case for most of the standard distributions.
A more complex example
Imagine a Bayesian Gaussian mixture model described as follows:
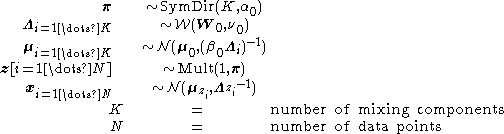
Note:- SymDir is the symmetric Dirichlet distribution of dimension
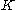 , with the hyperparameter for each component set to
, with the hyperparameter for each component set to 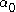 . The Dirichlet distribution is the conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
. The Dirichlet distribution is the conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
of the categorical distributionCategorical distributionIn probability theory and statistics, a categorical distribution is a probability distribution that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified...
or multinomial distribution. 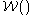 is the Wishart distribution, which is the conjugate prior of the precision matrix (inverse covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
is the Wishart distribution, which is the conjugate prior of the precision matrix (inverse covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
) for a multivariate Gaussian distribution.- Mult is a multinomial distribution over a single observation. The state space is a "one-of-K" representation, i.e. a
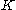 -dimensional vector in which one of the elements is 1 (specifying the identity of the observation) and all other elements are 0.
-dimensional vector in which one of the elements is 1 (specifying the identity of the observation) and all other elements are 0. 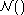 is the Gaussian distribution, in this case specifically the multivariate Gaussian distribution.
is the Gaussian distribution, in this case specifically the multivariate Gaussian distribution.
The interpretation of the above variables is as follows: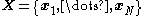 is the set of
is the set of 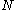 data points, each of which is a
data points, each of which is a 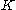 -dimensional vector distributed according to a multivariate Gaussian distribution.
-dimensional vector distributed according to a multivariate Gaussian distribution.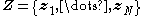 is a set of latent variables, one per data point, specifying which mixture component the corresponding data point belongs to, using a "one-of-K" vector representation with components
is a set of latent variables, one per data point, specifying which mixture component the corresponding data point belongs to, using a "one-of-K" vector representation with components 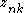 for
for 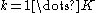 , as described above.
, as described above.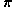 is the mixing proportions for the
is the mixing proportions for the 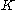 mixture components.
mixture components.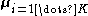 and
and 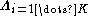 specify the parameters (meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
specify the parameters (meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and precisionPrecision (statistics)In statistics, the term precision can mean a quantity defined in a specific way. This is in addition to its more general meaning in the contexts of accuracy and precision and of precision and recall....
) associated with each mixture component.
The joint probability of all variables can be rewritten as
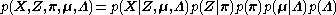
where the individual factors are
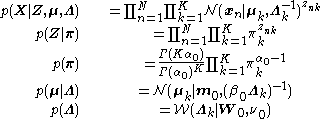
where
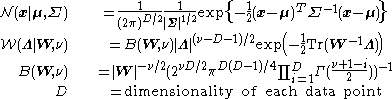
Assume that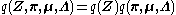 .
.
Then
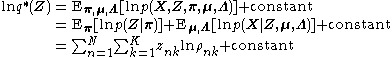
where we have defined
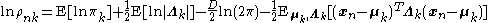
Exponentiating both sides of the formula for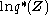 yields
yields
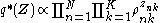
Requiring that this be normalized ends up requiring that the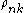 sum to 1 over all values of
sum to 1 over all values of 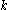 , yielding
, yielding
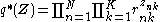
where
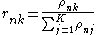
In other words,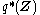 is a product of single-observation multinomial distributions, and factors over each individual
is a product of single-observation multinomial distributions, and factors over each individual 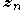 , which is distributed as a single-observation multinomial distribution with parameters
, which is distributed as a single-observation multinomial distribution with parameters 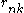 for
for 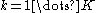 .
.
Furthermore, we note that
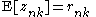
which is a standard result for categorical distributions.
Now, considering the factor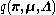 , note that it automatically factors into
, note that it automatically factors into 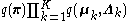 due to the structure of the graphical model defining our Gaussian mixture model, which is specified above.
due to the structure of the graphical model defining our Gaussian mixture model, which is specified above.
Then,
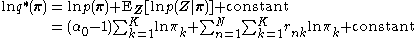
Taking the exponential of both sides, we recognize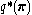 as a Dirichlet distribution
as a Dirichlet distribution
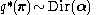
where
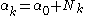
where
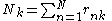
Finally
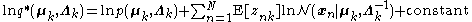
Grouping and reading off terms involving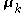 and
and 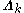 , the result is a Gaussian-Wishart distribution given by
, the result is a Gaussian-Wishart distribution given by
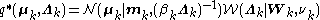
given the definitions
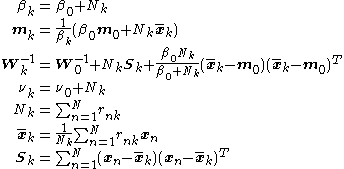
Finally, notice that these functions require the values of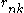 , which make use of
, which make use of 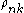 , which is defined in turn based on
, which is defined in turn based on 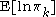 ,
, 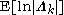 , and
, and 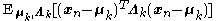 . Now that we have determined the distributions over which these expectations are taken, we can derive formulas for them:
. Now that we have determined the distributions over which these expectations are taken, we can derive formulas for them:
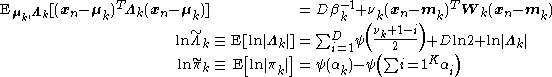
These results lead to
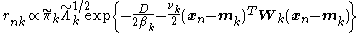
These can be converted from proportional to absolute values by normalizing over so that the corresponding values sum to 1.
so that the corresponding values sum to 1.
Note that:
- The update equations for the parameters
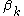 ,
, 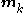 ,
, 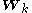 and
and 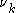 of the variables
of the variables 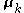 and
and 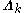 depend on the statistics
depend on the statistics 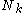 ,
, 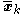 , and
, and 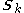 , and these statistics in turn depend on
, and these statistics in turn depend on 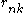 .
. - The update equations for the parameters
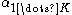 of the variable
of the variable 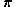 depend on the statistic
depend on the statistic 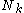 , which depends in turn on
, which depends in turn on 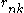 .
. - The update equation for
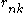 has a direct circular dependence on
has a direct circular dependence on 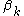 ,
, 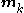 ,
, 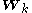 and
and 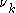 as well as an indirect circular dependence on
as well as an indirect circular dependence on 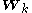 ,
, 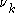 and
and  through
through 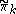 and
and 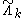 .
.
This suggests an iterative procedure that alternates between two steps:
- An E-step that computes the value of
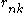 using the current values of all the other parameters.
using the current values of all the other parameters. - An M-step that uses the new value of
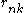 to compute new values of all the other parameters.
to compute new values of all the other parameters.
Note that these steps correspond closely with the standard EM algorithm to derive a maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
or maximum a posterioriMaximum a posterioriIn Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
(MAP) solution for the parameters of a Gaussian mixture model. The responsibilities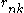 in the E step correspond closely to the posterior probabilitiesPosterior probabilityIn Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
in the E step correspond closely to the posterior probabilitiesPosterior probabilityIn Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
of the latent variables given the data, i.e.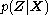 ; the computation of the statistics
; the computation of the statistics 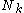 ,
, 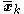 , and
, and 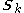 corresponds closely to the computation of corresponding "soft-count" statistics over the data; and the use of those statistics to compute new values of the parameters corresponds closely to the use of soft counts to compute new parameter values in normal EM over a Gaussian mixture model.
corresponds closely to the computation of corresponding "soft-count" statistics over the data; and the use of those statistics to compute new values of the parameters corresponds closely to the use of soft counts to compute new parameter values in normal EM over a Gaussian mixture model.
Exponential-family distributions
Note that in the previous example, once the distribution over unobserved variables was assumed to factorize into distributions over the "parameters" and distributions over the "latent data", the derived "best" distribution for each variable was in the same family as the corresponding prior distribution over the variable. This is a general result that holds true for all prior distributions derived from the exponential familyExponential familyIn probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
.
See also
- Variational message passingVariational message passingVariational message passing is an approximate inference technique for continuous- or discrete-valued Bayesian networks, with conjugate-exponential parents, developed by John Winn...
: a modular algorithm for variational Bayesian inference. - Expectation-maximization algorithmExpectation-maximization algorithmIn statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
: a related approach which corresponds to a special case of variational Bayesian inference.
External links
- Variational-Bayes Repository A repository of papers, software, and links related to the use of variational methods for approximate Bayesian learning
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay provides an introduction to variational methods (p. 422).
- Variational Algorithms for Approximate Bayesian Inference, by M. J. Beal includes comparisons of EM to Variational Bayesian EM and derivations of several models including Variational Bayesian HMMs.
- SymDir is the symmetric Dirichlet distribution of dimension

