.gif)
Moment (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" (in a particular sense) of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by an ellipsoid. Other moments describe other aspects of a distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
such as how the distribution is skewed from its mean, or peaked. The mathematical concept is closely related to the concept of moment
Moment (physics)
In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...
in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, although moment in physics is often represented somewhat differently. Any distribution can be characterized by a number of features (such as the mean, the variance, the skewness, etc.), and the moments of a function describe the nature of its distribution.
The 1st moment is denoted by μ1. The first moment of the distribution of the random variable X is the expectation operator, i.e., the population mean (if the first moment exists).
In higher orders, the central moments (moments about the mean) are more interesting than the moments about zero. The kth central moment
Central moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
, of a real-valued random variable probability distribution X, with the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ is:
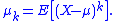
The first central moment is thus 0. The zero-th central moment, μ0 is one. See also central moment
Central moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
.
Other moments may also be defined. For example, the n th inverse moment about zero is
 and the n th logarithmic moment about zero is
and the n th logarithmic moment about zero is 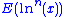 .
.Significance of the moments
The nth moment of a real-valued continuous function f(x) of a real variable about a value c is
It is possible to define moments for random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s in a more general fashion than moments for real values—see moments in metric spaces. The moment of a function, without further explanation, usually refers to the above expression with c = 0.
Usually, except in the special context of the problem of moments, the function f(x) will be a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
. The nth moment about zero of a probability density function f(x) is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of Xn and is called a raw moment or crude moment. The moments about its mean μ are called central moments
Central moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
; these describe the shape of the function, independently of translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
.
If f is a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
, then the value of the integral above is called the nth moment of the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. More generally, if F is a cumulative probability distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of any probability distribution, which may not have a density function, then the nth moment of the probability distribution is given by the Riemann–Stieltjes integral

where X is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
that has this distribution and E the expectation operator or mean.
When
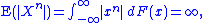
then the moment is said not to exist. If the nth moment about any point exists, so does (n − 1)th moment, and all lower-order moments, about every point.
Variance
The second central momentCentral moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
about the mean is the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
. Its positive square root is the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
σ.
Normalized moments
The normalized nth central moment or standardized moment is the nth central moment divided by σn; the normalized nth central moment of x = E((x − μ)n)/σn. These normalized central moments are dimensionless quantities, which represent the distribution independently of any linear change of scale.Skewness
The third central moment is a measure of the lopsidedness of the distribution; any symmetric distribution will have a third central moment, if defined, of zero. The normalized third central moment is called the skewnessSkewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
, often γ. A distribution that is skewed to the left (the tail of the distribution is heavier on the left) will have a negative skewness. A distribution that is skewed to the right (the tail of the distribution is heavier on the right), will have a positive skewness.
For distributions that are not too different from the normal distribution, the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
will be somewhere near μ − γσ/6; the mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
about μ − γσ/2.
Kurtosis
The fourth central moment is a measure of whether the distribution is tall and skinny or short and squat, compared to the normal distribution of the same variance. Since it is the expectation of a fourth power, the fourth central moment, where defined, is always non-negative; and except for a point distribution, it is always strictly positive. The fourth central moment of a normal distribution is 3σ4.The kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
κ is defined to be the normalized fourth central moment minus 3. (Equivalently, as in the next section, it is the fourth cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
divided by the square of the variance.) Some authorities do not subtract three, but it is usually more convenient to have the normal distribution at the origin of coordinates. If a distribution has a peak at the mean and long tails, the fourth moment will be high and the kurtosis positive (leptokurtic); and conversely; thus, bounded distributions tend to have low kurtosis (platykurtic).
The kurtosis can be positive without limit, but κ must be greater than or equal to γ2 − 2; equality only holds for binary distributions. For unbounded skew distributions not too far from normal, κ tends to be somewhere in the area of γ2 and 2γ2.
The inequality can be proven by considering

where T = (X − μ)/σ. This is the expectation of a square, so it is non-negative whatever a is; on the other hand, it's also a quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
in a. Its discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
must be non-positive, which gives the required relationship.
Mixed moments
Mixed moments are moments involving multiple variables.Some examples are covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
, coskewness and cokurtosis. While there is a unique covariance, there are multiple co-skewnesses and co-kurtoses.
Higher moments
High-order moments are moments beyond 4th-order moments. The higher the moment, the harder it is to estimate, in the sense that larger samples are required in order to obtain estimates of similar quality.Cumulants
The first moment and the second and third unnormalized central moments are additive in the sense that if X and Y are independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variables then
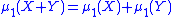
and
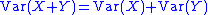
and
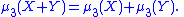
(These can also hold for variables that satisfy weaker conditions than independence. The first always holds; if the second holds, the variables are called uncorrelated
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
).
In fact, these are the first three cumulants and all cumulants share this additivity property.
Sample moments
The moments of a population can be estimated using the sample k-th moment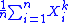
applied to a sample X1,X2,..., Xn drawn from the population.
It can be shown that the expected value of the sample moment is equal to the k-th moment of the population, if that moment exists, for any sample size n. It is thus an unbiased estimator.
Problem of moments
The problem of moments seeks characterizations of sequences { μ′n : n = 1, 2, 3, ... } that are sequences of moments of some function f.Partial moments
Partial moments are sometimes referred to as "one-sided moments." The nth order lower and upper partial moments with respect to a reference point r may be expressed as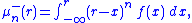
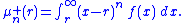
Partial moments are normalized by being raised to the power 1/n. The upside potential ratio
Upside potential ratio
The Upside-Potential Ratio is a measure of a return of an investment asset relative to the minimal acceptable return. The measurement allows a firm or individual to choose investments which have had relatively good upside performance, per unit of downside risk....
may be expressed as a ratio of a first-order upper partial moment to a normalized second-order lower partial moment.
Moments in metric spaces
Let (M, d) be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, and let B(M) be the Borel σ-algebra on M, the σ-algebra generated by the d-open subsets
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of M. (For technical reasons, it is also convenient to assume that M is a separable space with respect to the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
d.) Let 1 ≤ p ≤ +∞.
The pth moment of a measure μ on the measurable space (M, B(M)) about a given point x0 in M is defined to be
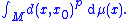
μ is said to have finite pth moment if the pth moment of μ about x0 is finite for some x0 ∈ M.
This terminology for measures carries over to random variables in the usual way: if (Ω, Σ, P) is a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
and X : Ω → M is a random variable, then the pth moment of X about x0 ∈ M is defined to be
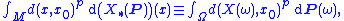
and X has finite pth moment if the pth moment of X about x0 is finite for some x0 ∈ M.
See also
- Hamburger moment problem
- Hausdorff moment problem
- Image momentsImage momentsIn image processing, computer vision and related fields, an image moment is a certain particular weighted average of the image pixels' intensities, or a function of such moments, usually chosen to have some attractive property or interpretation....
- L-momentL-momentIn statistics, L-moments are statistics used to summarize the shape of a probability distribution. They are analogous to conventional moments in that they can be used to calculate quantities analogous to standard deviation, skewness and kurtosis, termed the L-scale, L-skewness and L-kurtosis...
- Method of momentsMethod of momentsMethod of moments may refer to:* Method of moments , a method of parameter estimation in statistics* Method of moments , a way of proving convergence in distribution in probability theory...
- Second moment methodSecond moment methodIn mathematics, the second moment method is a technique used in probability theory and analysis to show that a random variable has positive probability of being positive...
- Standardized moment
- Stieltjes moment problem
- Taylor expansions for the moments of functions of random variablesTaylor expansions for the moments of functions of random variablesIn probability theory, it is possible to approximate the moments of a function f of a random variable X using Taylor expansions, provided that f is sufficiently differentiable and that the moments of X are finite...

