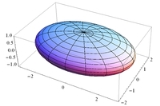
Ellipsoid
Overview
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
that is a higher dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al analogue of an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
. The equation of a standard axis-aligned ellipsoid body in an xyz-Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is

where a and b are the equatorial radii (along the x and y axes) and c is the polar radius (along the z-axis), all of which are fixed positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s determining the shape of the ellipsoid.
More generally, an arbitrarily oriented ellipsoid, centered at v, is defined by the equation
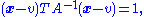
where A is a positive definite matrix and x, v are vectors.

