Separable space
Encyclopedia
In mathematics
a topological space
is called separable if it contains a countable
dense subset; that is, there exists a sequence
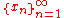of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
Like the other axioms of countability, separability is a "limitation on size", not necessarily in terms of cardinality (though, in the presence of the Hausdorff axiom
, this does turn out to be the case; see below) but in a more subtle topological sense. In particular, every continuous function
on a separable space whose image is a subset of a Hausdorff space is determined by its values on the countable dense subset.
In general, separability is a technical hypothesis on a space which is quite useful and — among the classes of spaces studied in geometry and classical analysis — generally considered to be quite mild. It is important to compare separability with the related notion of second countability, which is in general stronger but equivalent on the class of metrizable spaces.
, in which the rational numbers form a countable dense subset. Similarly the set of all vectors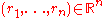
in which 
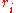is rational for all i is a countable dense subset of 
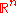; so for every 
the 
-dimensional Euclidean space
is separable.
A simple example of a space which is not separable is a discrete space
of uncountable cardinality.
Further examples are given below.
is separable: if
is a countable base, choosing any 
gives a countable dense subset. Conversely, a metrizable space is separable if and only if it is second countable, which is the case if and only if it is Lindelöf
.
To further compare these two properties:
is separable, as well as second countable, quasi-compact, and connected
. The "trouble" with the trivial topology is its poor separation properties: its Kolmogorov quotient is the one-point space.
A first countable, separable Hausdorff space (in particular, a separable metric space) has at most the continuum cardinality
c. In such a space, closure
is determined by limits of sequences and any sequence has at most one limit, so there is a surjective map from the set of convergent sequences with values in the countable dense subset to the points of X.
A separable Hausdorff space has cardinality at most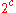
, where c is the cardinality of the continuum. For this closure is characterized in terms of limits of filter bases: if Y is a subset of X and z is a point of X, then z is in the closure of Y if and only if there exists a filter base B consisting of subsets of Y which converges to z. The cardinality of the set 
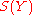of such filter bases is at most 
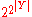. Moreover, in a Hausdorff space, there is at most one limit to every filter base. Therefore, there is a surjection 
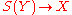when 
The same arguments establish a more general result: suppose that a Hausdorff topological space X contains a dense subset of cardinality
.
Then X has cardinality at most
and cardinality at most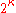 
if it is first countable.
The product of at most continuum many separable spaces is a separable space . In particular the space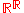
of all functions from the real line to itself, endowed with the product topology, is a separable Hausdorff space of cardinality 
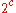. More generally, if κ is any infinite cardinal, then a product of at most 2κ spaces with dense subsets of size at most κ has itself a dense subset of size at most κ (Hewitt–Marczewski–Pondiczery theorem).
and constructive mathematics, since many theorems that can be proved for nonseparable spaces have constructive proofs only for separable spaces. Such constructive proofs can be turned into algorithm
s for use in numerical analysis, and they are the only sorts of proofs acceptable in constructive analysis. A famous example of a theorem of this sort is the Hahn–Banach theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is called separable if it contains a countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
dense subset; that is, there exists a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
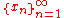of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.Like the other axioms of countability, separability is a "limitation on size", not necessarily in terms of cardinality (though, in the presence of the Hausdorff axiom
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, this does turn out to be the case; see below) but in a more subtle topological sense. In particular, every continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on a separable space whose image is a subset of a Hausdorff space is determined by its values on the countable dense subset.
In general, separability is a technical hypothesis on a space which is quite useful and — among the classes of spaces studied in geometry and classical analysis — generally considered to be quite mild. It is important to compare separability with the related notion of second countability, which is in general stronger but equivalent on the class of metrizable spaces.
First examples
Any topological space which is itself finite or countably infinite is separable, for the whole space is a countable dense subset of itself. An important example of an uncountable separable space is the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, in which the rational numbers form a countable dense subset. Similarly the set of all vectors
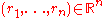in which 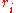is rational for all i is a countable dense subset of 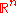; so for every the -dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is separable.
A simple example of a space which is not separable is a discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
of uncountable cardinality.
Further examples are given below.
Separability versus second countability
Any second-countable spaceSecond-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
is separable: if
is a countable base, choosing any gives a countable dense subset. Conversely, a metrizable space is separable if and only if it is second countable, which is the case if and only if it is LindelöfLindelöf space
In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
.
To further compare these two properties:
- An arbitrary subspace of a second countable space is second countable; subspaces of separable spaces need not be separable (see below).
- Any continuous image of a separable space is separable .; even a quotient of a second countable space need not be second countable.
- A productProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of at most continuum many separable spaces is separable. A countable product of second countable spaces is second countable, but an uncountable product of second countable spaces need not even be first countable.
Cardinality
The property of separability does not in and of itself give any limitations on the cardinality of a topological space: any set endowed with the trivial topologyTrivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
is separable, as well as second countable, quasi-compact, and connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. The "trouble" with the trivial topology is its poor separation properties: its Kolmogorov quotient is the one-point space.
A first countable, separable Hausdorff space (in particular, a separable metric space) has at most the continuum cardinality
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
c. In such a space, closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
is determined by limits of sequences and any sequence has at most one limit, so there is a surjective map from the set of convergent sequences with values in the countable dense subset to the points of X.
A separable Hausdorff space has cardinality at most
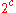, where c is the cardinality of the continuum. For this closure is characterized in terms of limits of filter bases: if Y is a subset of X and z is a point of X, then z is in the closure of Y if and only if there exists a filter base B consisting of subsets of Y which converges to z. The cardinality of the set 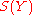of such filter bases is at most 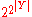. Moreover, in a Hausdorff space, there is at most one limit to every filter base. Therefore, there is a surjection 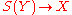when The same arguments establish a more general result: suppose that a Hausdorff topological space X contains a dense subset of cardinality
.Then X has cardinality at most
and cardinality at most 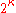if it is first countable.The product of at most continuum many separable spaces is a separable space . In particular the space
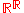of all functions from the real line to itself, endowed with the product topology, is a separable Hausdorff space of cardinality 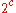. More generally, if κ is any infinite cardinal, then a product of at most 2κ spaces with dense subsets of size at most κ has itself a dense subset of size at most κ (Hewitt–Marczewski–Pondiczery theorem).Constructive mathematics
Separability is especially important in numerical analysisNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
and constructive mathematics, since many theorems that can be proved for nonseparable spaces have constructive proofs only for separable spaces. Such constructive proofs can be turned into algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s for use in numerical analysis, and they are the only sorts of proofs acceptable in constructive analysis. A famous example of a theorem of this sort is the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
.
Separable spaces
- Every compact metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(or metrizable space) is separable. - The space of all continuous functions from a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subset of Rn into R is separable. - The Lebesgue spaces Lp are separable for any 1 ≤ p < ∞.
- Any topological space which is the union of a countable number of separable subspaces is separable. Together, these first two examples give a different proof that n-dimensional Euclidean space is separable.
- It follows easily from the Weierstrass approximation theoremStone-Weierstrass theoremIn mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function...
that the set Q[t] of polynomials with rational coefficients is a countable dense subset of the space C([0,1]) of continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1] with the metric of uniform convergence. The Banach-Mazur theoremBanach-Mazur theoremIn mathematics, the Banach–Mazur theorem is a theorem of functional analysis. Very roughly, it states that most well-behaved normed spaces are subspaces of the space of continuous paths...
asserts that any separable Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
is isometrically isomorphic to a closed linear subspaceLinear subspaceThe concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of C([0,1]). - A Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is separable if and only if it has a countable orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
, it follows that any separable, infinite-dimensional Hilbert space is isometric to ℓ2. - An example of a separable space that is not second-countable is Rllt, the set of real numbers equipped with the lower limit topologyLower limit topologyIn mathematics, the lower limit topology or right half-open interval topology is a topology defined on the set R of real numbers; it is different from the standard topology on R and has a number of interesting properties...
.
Non-separable spaces
- The first uncountable ordinal ω1First uncountable ordinalIn mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
in its order topologyOrder topologyIn mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
is not separable. - The Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
l∞ of all bounded real sequences, with the supremum norm, is not separable. The same holds for L∞. - The Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of functions of bounded variationBounded variationIn mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
, is not separable: note however that this space has very important applications in mathematicsMathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineeringEngineeringEngineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
.
Properties
- A subspace of a separable space need not be separable (see the Sorgenfrey plane and the Moore planeMoore planeIn mathematics, the Moore plane, also sometimes called Niemytzki plane is a topological space. It is a completely regular Hausdorff space which is not normal...
), but every open subspace of a separable space is separable, . Also every subspace of a separable metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is separable. - In fact, every topological space is a subspace of a separable space of the same cardinality. A construction adding at most countably many points is given in .
- The set of all real-valued continuous functions on a separable space has a cardinality less than or equal to c. This follows since such functions are determined by their values on dense subsets.
- From the above property, one can deduce the following: If X is a separable space having an uncountable closed discrete subspace, then X cannot be normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. This shows that the Sorgenfrey plane is not normal. - For a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
space X, the following are equivalent:
-
- (i) X is second countable.
- (ii) The space
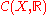of continuous real-valued functions on X with the supremum norm is separable. - (iii) X is metrizable.
Embedding separable metric spaces
- Every separable metric space is homeomorphic to a subset of the Hilbert cubeHilbert cubeIn mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology...
. This is established in the proof of the Urysohn metrization theorem. - Every separable metric space is isometricIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to a subset of the (non-separable) Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
l∞ of all bounded real sequences with the supremum norm; this is known as the Fréchet embedding. - Every separable metric space is isometric to a subset of C([0,1]), the separable Banach space of continuous functions [0,1]→R, with the supremum norm. This is due to Stefan BanachStefan BanachStefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
. - Every separable metric space is isometric to a subset of the Urysohn universal spaceUrysohn universal spaceThe Urysohn universal space is a certain metric space that contains all separable metric spaces in a particularly nice manner. This mathematics concept is due to Pavel Samuilovich Urysohn.-Definition:...
, a completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
separable space with a certain homogeneity.