Hilbert cube
Encyclopedia
In mathematics
, the Hilbert cube, named after David Hilbert
, is a topological space
that provides an instructive example of some ideas in topology
. Furthermore, many interesting topological spaces can be embedded in the Hilbert cube; that is, can be viewed as subspaces of the Hilbert cube (see below).
[0, 1/n] for n = 1, 2, 3, 4, ... That is, it is a cuboid
of countably infinite dimension
, where the lengths of the edges in each orthogonal direction form the sequence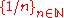
.
The Hilbert cube is homeomorphic
to the product of countably infinitely many copies of the unit interval
[0, 1]. In other words, it is topologically indistinguishable from the unit cube
of countably infinite dimension.
If a point in the Hilbert cube is specified by a sequence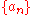
with 
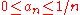, then a homeomorphism to the infinite dimensional unit cube is given by 
.
, indeed as a specific subset of a Hilbert space
with countably infinite dimension.
For these purposes, it's best not to think of it as a product of copies of [0,1], but instead as
as stated above, for topological properties, this makes no difference.
That is, an element of the Hilbert cube is an infinite sequence
that satisfies
Any such sequence belongs to the Hilbert space ℓ2
, so the Hilbert cube inherits a metric from there. One can show that the topology induced by the metric is the same as the product topology
in the above definition.
s, the Hilbert cube is itself a compact Hausdorff space as a result of the Tychonoff theorem.
In ℓ2, no point has a compact neighbourhood (thus, ℓ2 is not locally compact). One might expect that all of the compact subsets of ℓ2 are finite-dimensional.
The Hilbert cube shows that this is not the case.
But the Hilbert cube fails to be a neighbourhood of any point p because its side becomes smaller and smaller in each dimension, so that an open ball around p of any fixed radius e > 0 must go outside the cube in some dimension.
Every subset of the Hilbert cube inherits from the Hilbert cube the properties of being both metrizable (and therefore T4
) and second countable. It is more interesting that the converse also holds: Every second countable T4
space is homeomorphic to a subset of the Hilbert cube.
Trivially, every Gδ-subset of the Hilbert cube is a Polish space
, a topological space homeomorphic to a complete metric space. Conversely, every Polish space is homeomorphic to a Gδ-subset of the Hilbert cube.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hilbert cube, named after David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that provides an instructive example of some ideas in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Furthermore, many interesting topological spaces can be embedded in the Hilbert cube; that is, can be viewed as subspaces of the Hilbert cube (see below).
Definition
The Hilbert cube is best defined a topological product of the intervalsInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0, 1/n] for n = 1, 2, 3, 4, ... That is, it is a cuboid
Cuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
of countably infinite dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, where the lengths of the edges in each orthogonal direction form the sequence
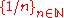.The Hilbert cube is homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the product of countably infinitely many copies of the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0, 1]. In other words, it is topologically indistinguishable from the unit cube
Unit cube
A unit cube, sometimes called a cube of side 1, is a cube whose sides are 1 unit long. The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units.- Unit Hypercube :...
of countably infinite dimension.
If a point in the Hilbert cube is specified by a sequence
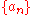with 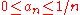, then a homeomorphism to the infinite dimensional unit cube is given by .The Hilbert cube as a metric space
It's sometimes convenient to think of the Hilbert cube as a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, indeed as a specific subset of a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
with countably infinite dimension.
For these purposes, it's best not to think of it as a product of copies of [0,1], but instead as
- [0,1] × [0,1/2] × [0,1/3] × ···;
as stated above, for topological properties, this makes no difference.
That is, an element of the Hilbert cube is an infinite sequence
that satisfies
- 0 ≤ xn ≤ 1/n.
Any such sequence belongs to the Hilbert space ℓ2
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, so the Hilbert cube inherits a metric from there. One can show that the topology induced by the metric is the same as the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
in the above definition.
Properties
As a product of compact Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s, the Hilbert cube is itself a compact Hausdorff space as a result of the Tychonoff theorem.
In ℓ2, no point has a compact neighbourhood (thus, ℓ2 is not locally compact). One might expect that all of the compact subsets of ℓ2 are finite-dimensional.
The Hilbert cube shows that this is not the case.
But the Hilbert cube fails to be a neighbourhood of any point p because its side becomes smaller and smaller in each dimension, so that an open ball around p of any fixed radius e > 0 must go outside the cube in some dimension.
Every subset of the Hilbert cube inherits from the Hilbert cube the properties of being both metrizable (and therefore T4
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
) and second countable. It is more interesting that the converse also holds: Every second countable T4
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
space is homeomorphic to a subset of the Hilbert cube.
Trivially, every Gδ-subset of the Hilbert cube is a Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
, a topological space homeomorphic to a complete metric space. Conversely, every Polish space is homeomorphic to a Gδ-subset of the Hilbert cube.