Unit interval
Encyclopedia
In mathematics
, the unit interval is the closed interval
, that is, the set of all real number
s that are greater than or equal to 0 and less than or equal to 1. It is often denoted (capital letter I).
In addition to its role in real analysis
, the unit interval is used to study homotopy theory in the field of topology
.
In the literature, the term "unit interval" is sometimes applied to the other shapes that an interval from 0 to 1 could take: , , and However, the notation is most commonly reserved for the closed interval .
to the extended real number line
. As a topological space
it is compact
, contractible, path connected
and locally path connected
. The Hilbert cube
is obtained by taking a topological product of countably many copies of the unit interval.
In mathematical analysis, the unit interval is a one-dimensional
analytical manifold
whose boundary consists of the two points 0 and 1. Its standard orientation
goes from 0 to 1.
The unit interval is a totally ordered set
and a complete lattice
(every subset of the unit interval has a supremum
and an infimum
).
The unit interval is a subset
of the real number
s
. However, it has the same size as the whole set: the cardinality of the continuum
. Since the real numbers can be used to represent points along an infinitely long line
, this implies that a line segment
of length 1, which is a part of that line, has the same number of points as the whole line. Moreover, it has the same number of points as a square of area
1, as a cube
of volume
1, and even as an unbounded n-dimensional Euclidean space
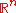(see Space filling curve).
The number of elements (either real numbers or points) in all the above-mentioned sets is uncountable
, as it is strictly greater than the number of natural number
s.
s, the (analogue of the) unit interval is the graph whose vertex set is {0,1} and which contains a single edge e whose source is 0 and whose target is 1. One can then define a notion of homotopy
between quiver homomorphism
s analogous to the notion of homotopy between continuous maps.
{0,1}, in which case rather than only taking values 0 or 1, any value between and including 0 and 1 can be assumed. Algebraically, negation (NOT) is replaced with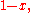
conjunction (AND) is replaced with multiplication (
), and disjunction (OR) is defined via De Morgan's law.
Interpreting these values as logical truth values yields a multi-valued logic
, which forms the basis for fuzzy logic
and probabilistic logic
. In these interpretations, a value is interpreted as the "degree" of truth – to what extent a proposition is true, or the probability that the proposition is true.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the unit interval is the closed interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
, that is, the set of all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s that are greater than or equal to 0 and less than or equal to 1. It is often denoted (capital letter I).
In addition to its role in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, the unit interval is used to study homotopy theory in the field of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
In the literature, the term "unit interval" is sometimes applied to the other shapes that an interval from 0 to 1 could take: , , and However, the notation is most commonly reserved for the closed interval .
Properties
The unit interval is a complete metric space, homeomorphicHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
. As a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
it is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, contractible, path connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
and locally path connected
Locally connected space
In topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
. The Hilbert cube
Hilbert cube
In mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology...
is obtained by taking a topological product of countably many copies of the unit interval.
In mathematical analysis, the unit interval is a one-dimensional
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
analytical manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
whose boundary consists of the two points 0 and 1. Its standard orientation
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
goes from 0 to 1.
The unit interval is a totally ordered set
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
and a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
(every subset of the unit interval has a supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
and an infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
).
Cardinality
The size or cardinality of a set is the number of elements it contains.The unit interval is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
. However, it has the same size as the whole set: the cardinality of the continuumCardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
. Since the real numbers can be used to represent points along an infinitely long line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, this implies that a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
of length 1, which is a part of that line, has the same number of points as the whole line. Moreover, it has the same number of points as a square of area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
1, as a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
of volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
1, and even as an unbounded n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
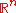(see Space filling curve).The number of elements (either real numbers or points) in all the above-mentioned sets is uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
, as it is strictly greater than the number of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s.
Generalizations
Sometimes, the term "unit interval" is used to refer to objects that play a role in various branches of mathematics analogous to the role that [0,1] plays in homotopy theory. For example, in the theory of quiverQuiver (mathematics)
In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation, V, of a quiver assigns a vector space V to each vertex x of the quiver and a linear map V to each...
s, the (analogue of the) unit interval is the graph whose vertex set is {0,1} and which contains a single edge e whose source is 0 and whose target is 1. One can then define a notion of homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
between quiver homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s analogous to the notion of homotopy between continuous maps.
Fuzzy logic
In logic, the unit interval [0,1] can be interpreted as a generalization of the Boolean domainBoolean domain
In mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true...
{0,1}, in which case rather than only taking values 0 or 1, any value between and including 0 and 1 can be assumed. Algebraically, negation (NOT) is replaced with
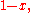conjunction (AND) is replaced with multiplication (), and disjunction (OR) is defined via De Morgan's law.Interpreting these values as logical truth values yields a multi-valued logic
Multi-valued logic
In logic, a many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition...
, which forms the basis for fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
and probabilistic logic
Probabilistic logic
The aim of a probabilistic logic is to combine the capacity of probability theory to handle uncertainty with the capacity of deductive logic to exploit structure. The result is a richer and more expressive formalism with a broad range of possible application areas...
. In these interpretations, a value is interpreted as the "degree" of truth – to what extent a proposition is true, or the probability that the proposition is true.