Boolean domain
Encyclopedia
In mathematics
and abstract algebra
, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true. In logic
, mathematics and theoretical computer science
, a Boolean domain is usually written as {0,1}, as {false, true}, {F, T} (or similar), or as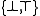
.
The algebraic structure
that naturally builds on a Boolean domain is the Boolean algebra with two elements. The initial object
in the category
of bounded lattices is a Boolean domain. The Sierpiński space
, a certain topological space
with two elements, resembles a Boolean domain.
In computer science
, a Boolean variable is a variable
that takes values in some Boolean domain. Some programming language
s feature reserved word
s or symbols for the elements of the Boolean domain, for example
in the strict sense. In C
or BASIC
, for example, falsity is represented by the number 0 and truth is represented by the number 1 or -1, respectively, and all variables that can take these values can also take any other numerical values.
[0,1], in which case rather than only taking values 0 or 1, any value between and including 0 and 1 can be assumed. Algebraically, negation (NOT) is replaced with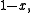
conjunction (AND) is replaced with multiplication (
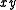), and disjunction (OR) is defined via De Morgan's law.
Interpreting these values as logical truth values yields a multi-valued logic
, which forms the basis for fuzzy logic
and probabilistic logic
. In these interpretations, a value is interpreted as the "degree" of truth – to what extent a proposition is true, or the probability that the proposition is true.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true. In logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, mathematics and theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, a Boolean domain is usually written as {0,1}, as {false, true}, {F, T} (or similar), or as
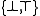.The algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
that naturally builds on a Boolean domain is the Boolean algebra with two elements. The initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of bounded lattices is a Boolean domain. The Sierpiński space
Sierpinski space
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
, a certain topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
with two elements, resembles a Boolean domain.
In computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a Boolean variable is a variable
Variable (programming)
In computer programming, a variable is a symbolic name given to some known or unknown quantity or information, for the purpose of allowing the name to be used independently of the information it represents...
that takes values in some Boolean domain. Some programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s feature reserved word
Reserved word
Reserved words are one type of grammatical construct in programming languages. These words have special meaning within the language and are predefined in the language’s formal specifications...
s or symbols for the elements of the Boolean domain, for example
false and true. However, many programming languages do not have a Boolean datatypeBoolean datatype
In computer science, the Boolean or logical data type is a data type, having two values , intended to represent the truth values of logic and Boolean algebra...
in the strict sense. In C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
or BASIC
BASIC
BASIC is a family of general-purpose, high-level programming languages whose design philosophy emphasizes ease of use - the name is an acronym from Beginner's All-purpose Symbolic Instruction Code....
, for example, falsity is represented by the number 0 and truth is represented by the number 1 or -1, respectively, and all variables that can take these values can also take any other numerical values.
Generalizations
The Boolean domain {0,1} can be replaced by the unit intervalUnit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1], in which case rather than only taking values 0 or 1, any value between and including 0 and 1 can be assumed. Algebraically, negation (NOT) is replaced with
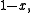conjunction (AND) is replaced with multiplication (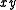), and disjunction (OR) is defined via De Morgan's law.Interpreting these values as logical truth values yields a multi-valued logic
Multi-valued logic
In logic, a many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition...
, which forms the basis for fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
and probabilistic logic
Probabilistic logic
The aim of a probabilistic logic is to combine the capacity of probability theory to handle uncertainty with the capacity of deductive logic to exploit structure. The result is a richer and more expressive formalism with a broad range of possible application areas...
. In these interpretations, a value is interpreted as the "degree" of truth – to what extent a proposition is true, or the probability that the proposition is true.