
Sierpinski space
Encyclopedia
In mathematics
, the Sierpiński space (or the connected two-point set) is a finite topological space
with two points, only one of which is closed
.
It is the smallest example of a topological space
which is neither trivial
nor discrete. It is named after Wacław Sierpiński.
The Sierpiński space has important relations to the theory of computation
and semantics
.
S whose underlying point set is {0,1} and whose open set
s are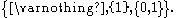
The closed set
s are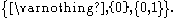
So the singleton set {0} is closed (but not open) and the set {1} is open (but not closed).
The closure operator
on S is determined by
A finite topological space is also uniquely determined by its specialization preorder. For the Sierpiński space this preorder
is actually a partial order and given by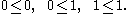
(with particular point 1) and the finite excluded point topology
(with excluded point 0). Therefore S has many properties in common with one or both of these families.
from X to the set {0,1} is typically denoted 2X. These functions are precisely the characteristic functions of X. Each such function is of the form
where U is a subset
of X. In other words, the set of functions 2X is in bijective correspondence with P(X), the power set of X. Every subset U of X has its characteristic function χU and every function from X to {0,1} is of this form.
Now suppose X is a topological space and let {0,1} have the Sierpiński topology. Then a function χU : X → S is continuous if and only if χU−1(1) is open in X. But, by definition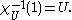
So χU is continuous if and only if U is open in X. Let C(X,S) denote the set of all continuous maps from X to S and let T(X) denote the topology of X (i.e. the family of all open sets). Then we have a bijection from T(X) to C(X,S) which sends the open set U to χU.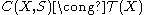
That is, if we identify 2X with P(X), the subset of continuous maps C(X,S) ⊂ 2X is precisely the topology of X: T(X) ⊂ P(X).
. There is contravariant functor T : Top → Set from the category of topological spaces
to the category of sets
which assigns each topological space X its set of open sets T(X) and each continuous function f : X → Y the preimage map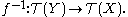
The statement then becomes: the functor T is represented
by (S, {1}) where S is the Sierpiński space. That is, T is naturally isomorphic to the Hom functor
Hom(–, S) with the natural isomorphism determined by the universal element {1} ∈ T(S).
induced by the family C(X,S) of continuous functions to Sierpiński space. Indeed, in order to coarsen the topology on X one must remove open sets. But removing the open set U would render χU discontinuous. So X has the coarsest topology for which each function in C(X,S) is continuous.
The family of functions C(X,S) separates points
in X if and only if X is a T0 space. Two points x and y will be separated by the function χU if and only if the open set U contains precisely one of the two points. This is exactly what it means for x and y to be topologically distinguishable.
Therefore if X is T0, we can embed X as a subspace of a product
of Sierpiński spaces, where there is one copy of S for each open set U in X. The embedding map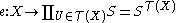
is given by
Since subspaces and products of T0 spaces are T0, it follows that a topological space is T0 if and only if it is homeomorphic to a subspace of a power of S.
the Sierpiński space arises as the spectrum
, Spec(R), of a discrete valuation ring
R such as Z(2) (the localization
of the integer
s at the prime ideal
generated by 2). The generic point
of Spec(R), coming from the zero ideal, corresponds to the open point 1, while the special point of Spec(R), coming from the unique maximal ideal
, corresponds to the closed point 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Sierpiński space (or the connected two-point set) is a finite topological space
Finite topological space
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
with two points, only one of which is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
.
It is the smallest example of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
which is neither trivial
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
nor discrete. It is named after Wacław Sierpiński.
The Sierpiński space has important relations to the theory of computation
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
and semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
.
Definition and fundamental properties
Explicitly, the Sierpiński space is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
S whose underlying point set is {0,1} and whose open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s are
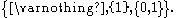
The closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s are
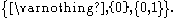
So the singleton set {0} is closed (but not open) and the set {1} is open (but not closed).
The closure operator
Kuratowski closure axioms
In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
on S is determined by

A finite topological space is also uniquely determined by its specialization preorder. For the Sierpiński space this preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
is actually a partial order and given by
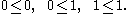
Topological properties
The Sierpiński space S is a special case of both the finite particular point topologyParticular point topology
In mathematics, the particular point topology is a topology where sets are considered open if they are empty or contain a particular, arbitrarily chosen, point of the topological space. Formally, let X be any set and p ∈ X. The collectionof subsets of X is then the particular point topology...
(with particular point 1) and the finite excluded point topology
Excluded point topology
In mathematics, the excluded point topology is a topology where exclusion of a particular point defines openness. Formally, let X be any set and p ∈ X. The collectionof subsets of X is then the excluded point topology on X....
(with excluded point 0). Therefore S has many properties in common with one or both of these families.
Separation
- The points 0 and 1 are topologically distinguishable in S since {1} is an open set which contains only one of these points. Therefore S is a Kolmogorov (T0) spaceKolmogorov spaceIn topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
. - However, S is not T1 since the point 1 is not closed. It follows that S is not HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, or Tn for any n ≥ 1. - S is not regularRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
(or completely regular) since the point 1 and the disjoint closed set {0} cannot be separated by neighborhoods. (Also regularity in the presence of T0 would imply Hausdorff.) - S is vacuouslyVacuous truthA vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
and completely normal since there are no nonempty separated sets. - S is not perfectly normal since the disjoint closed sets ∅ and {0} cannot be precisely separated by a function. Indeed {0} cannot be the zero set of any continuous function S → R since every such function is constantConstant functionIn mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
.
Connectedness
- The Sierpiński space S is both hyperconnected (since every nonempty open set contains 1) and ultraconnected (since every nonempty closed set contains 0).
- It follows that S is both connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
and path connected. - A pathPath (topology)In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
from 0 to 1 in S is given by the function: f(0) = 0 and f(t) = 1 for t > 0. The function f : I → S is continuous since f−1(1) = (0,1] which is open in I. - Like all finite topological spaces, S is locally path connected.
- The Sierpiński space is contractibleContractible spaceIn mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
, so the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of S is trivialTrivial groupIn mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
(as are all the higher homotopy groups).
Compactness
- Like all finite topological spaces, the Sierpiński space is both compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and second-countable. - The compact subset {1} of S is not closed showing that compact subsets of T0 spaces need not be closed.
- Every open cover of S must contain S itself since S is the only open neighborhood of 0. Therefore every open cover of S has an open subcover consisting of a single set: {S}.
- It follows that S is fully normal.
Convergence
- Every sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
in S convergesLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to the point 0. This is because the only neighborhood of 0 is S itself. - A sequence in S converges to 1 if and only if the sequence contains only finitely many terms equal to 0 (i.e. the sequence is eventually just 1's).
- The point 1 is a cluster point of a sequence in S if and only if the sequence contains infinitely many 1's.
- Examples:
- 1 is not a cluster point of (0,0,0,0,…).
- 1 is a cluster point (but not a limit) of (0,1,0,1,0,1,…).
- The sequence (1,1,1,1,…) converges to both 0 and 1.
Metrizability
- The Sierpiński space S is not metrizable or even pseudometrizable since it is not regular.
- S is generated by the hemimetric (or pseudoPseudometric spaceIn mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
-quasimetric)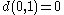 and
and 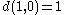 .
.
Other properties
- There are only three continuous maps from S to itself: the identity mapIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
and the constant maps to 0 and 1. - It follows that the homeomorphism groupHomeomorphism groupIn mathematics, particularly topology, the homeomorphism group of a topological space is the group consisting of all homeomorphisms from the space to itself with function composition as the group operation. Homeomorphism groups are very important in the theory of topological spaces and in general...
of S is trivialTrivial groupIn mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
.
Continuous functions to the Sierpiński space
Let X be an arbitrary set. The set of all functionsFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
from X to the set {0,1} is typically denoted 2X. These functions are precisely the characteristic functions of X. Each such function is of the form

where U is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of X. In other words, the set of functions 2X is in bijective correspondence with P(X), the power set of X. Every subset U of X has its characteristic function χU and every function from X to {0,1} is of this form.
Now suppose X is a topological space and let {0,1} have the Sierpiński topology. Then a function χU : X → S is continuous if and only if χU−1(1) is open in X. But, by definition
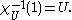
So χU is continuous if and only if U is open in X. Let C(X,S) denote the set of all continuous maps from X to S and let T(X) denote the topology of X (i.e. the family of all open sets). Then we have a bijection from T(X) to C(X,S) which sends the open set U to χU.
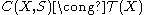
That is, if we identify 2X with P(X), the subset of continuous maps C(X,S) ⊂ 2X is precisely the topology of X: T(X) ⊂ P(X).
Categorical description
The above construction can be described nicely using the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. There is contravariant functor T : Top → Set from the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
to the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
which assigns each topological space X its set of open sets T(X) and each continuous function f : X → Y the preimage map
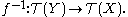
The statement then becomes: the functor T is represented
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
by (S, {1}) where S is the Sierpiński space. That is, T is naturally isomorphic to the Hom functor
Hom functor
In mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.-Formal...
Hom(–, S) with the natural isomorphism determined by the universal element {1} ∈ T(S).
The initial topology
Any topological space X has the initial topologyInitial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
induced by the family C(X,S) of continuous functions to Sierpiński space. Indeed, in order to coarsen the topology on X one must remove open sets. But removing the open set U would render χU discontinuous. So X has the coarsest topology for which each function in C(X,S) is continuous.
The family of functions C(X,S) separates points
Separating set
In mathematics a set of functions S from a set D to a set C is called a separating set for D or said to separate the points of D if for any two distinct elements x and y of D, there exists a function f in S so that f ≠ f.- Examples :* The singleton set consisting of the identity function on R...
in X if and only if X is a T0 space. Two points x and y will be separated by the function χU if and only if the open set U contains precisely one of the two points. This is exactly what it means for x and y to be topologically distinguishable.
Therefore if X is T0, we can embed X as a subspace of a product
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of Sierpiński spaces, where there is one copy of S for each open set U in X. The embedding map
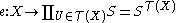
is given by

Since subspaces and products of T0 spaces are T0, it follows that a topological space is T0 if and only if it is homeomorphic to a subspace of a power of S.
In algebraic geometry
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
the Sierpiński space arises as the spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
, Spec(R), of a discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
R such as Z(2) (the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s at the prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
generated by 2). The generic point
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
of Spec(R), coming from the zero ideal, corresponds to the open point 1, while the special point of Spec(R), coming from the unique maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
, corresponds to the closed point 0.

