Kuratowski closure axioms
Encyclopedia
In topology
and related branches of mathematics
, the Kuratowski closure axioms are a set of axiom
s which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set
definition. They were first introduced by Kazimierz Kuratowski
, in a slightly different form that applied only to Hausdorff space
s.
A similar set of axioms can be used to define a topological structure using only the dual notion of interior operator.
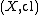is a set 
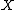with a function
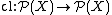
called the closure operator where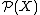
is the power set of 
.
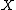The closure operator has to satisfy the following properties for all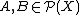
If the second axiom, that of idempotence, is relaxed, then the axioms define a preclosure operator
.
is called continuous
if for all subsets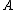
of 
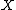
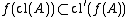
A point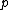
is called close to 
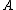in 
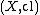if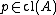 
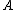is called closed
in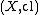
if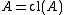 
. In other words the closed sets of 
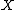are the fixed point
s of the closure operator.
If one takes an "open set" to be a set whose complement is closed, then the family of all open sets forms a topology
. Conversely, any topology can be induced in this way by the correct choice of closure operator.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Kuratowski closure axioms are a set of axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
definition. They were first introduced by Kazimierz Kuratowski
Kazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
, in a slightly different form that applied only to Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s.
A similar set of axioms can be used to define a topological structure using only the dual notion of interior operator.
Definition
A topological space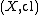 is a set 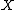with a function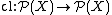called the closure operator where
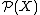is the power set of 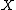.The closure operator has to satisfy the following properties for all
-
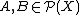
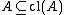(Extensivity) -
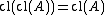(Idempotence) -
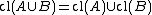(Preservation of binary unions) -
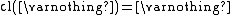(Preservation of nullary unions)
If the second axiom, that of idempotence, is relaxed, then the axioms define a preclosure operator
Preclosure operator
In topology, a preclosure operator, or Čech closure operator is a map between subsets of a set, similar to a topological closure operator, except that it is not required to be idempotent...
.
Recovering topological definitions
A function between two topological spacesis called continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
if for all subsets
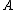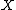
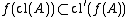
of A point
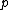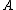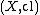is called close to in if 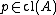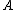is called closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
in
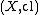if 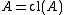. In other words the closed sets of 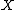are the fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of the closure operator.
If one takes an "open set" to be a set whose complement is closed, then the family of all open sets forms a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. Conversely, any topology can be induced in this way by the correct choice of closure operator.