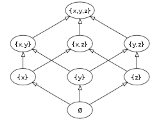
Power set
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the power set (or powerset) of any set S, written
 , P(S), ℘
, P(S), ℘Weierstrass p
In mathematics, the Weierstrass p , also called pe, is used for the Weierstrass's elliptic function. It is occasionally used for the power set, although for that purpose a cursive capital, rather than lower-case, p is more widespread...
(S) or 2S, is the set of all subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of S, including the empty set and S itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is postulated by the axiom of power set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
.
Any subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
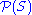 is called a family of sets
is called a family of setsFamily of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
over S.
Example
If S is the set {x, y, z}, then the subsets of S are:- {} (also denoted
 , the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
) - {x}
- {y}
- {z}
- {x, y}
- {x, z}
- {y, z}
- {x, y, z}
and hence the power set of
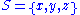 is
is
Properties
If S is a finite set with |S| = n elements, then the power set of S contains elements. This can be proved by mathematical induction
elements. This can be proved by mathematical inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
on n.
Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
shows that the power set of a set (whether infinite or not) always has strictly higher cardinality than the set itself (informally the power set must be larger than the original set). In particular, Cantor's theorem
Cantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
shows that the power set of a countably infinite
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
set is uncountably infinite. For example, the power set of the set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s can be put in a one-to-one correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
with the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (see cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
).
The power set of a set S, together with the operations of union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
, intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
and complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
can be viewed as the prototypical example of a Boolean algebra. In fact, one can show that any finite Boolean algebra is isomorphic to the Boolean algebra of the power set of a finite set. For infinite Boolean algebras this is no longer true, but every infinite Boolean algebra can be represented as a subalgebra of a power set Boolean algebra (see Stone's representation theorem).
The power set of a set S forms an Abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
when considered with the operation of symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
(with the empty set as the identity element and each set being its own inverse) and a commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
when considered with the operation of intersection. It can hence be shown (by proving the distributive laws) that the power set considered together with both of these operations forms a Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
.
Representing subsets as functions
In set theory, XY is the set of all function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from Y to X. As "2" can be defined as {0,1} (see natural number), 2S (i.e., {0,1}S) is the set of all function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from S to {0,1}. By identifying a function in 2S with the corresponding preimage of 1, we see that there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between 2S and
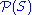 , where each function is the characteristic function of the subset in
, where each function is the characteristic function of the subset in  with which it is identified. Hence 2S and
with which it is identified. Hence 2S and 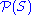 could be considered identical set-theoretically. (Thus there are two distinct notational motivations for denoting the power set by 2S: the fact that this function-representation of subsets makes it a special case of the XY notation and the property, mentioned above, that |2S| = 2|S|.)
could be considered identical set-theoretically. (Thus there are two distinct notational motivations for denoting the power set by 2S: the fact that this function-representation of subsets makes it a special case of the XY notation and the property, mentioned above, that |2S| = 2|S|.)This notion can be applied to the example above in which
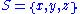 to see the isomorphism with the binary numbers
to see the isomorphism with the binary numbersfrom 0 to 2n−1 with n being the number of elements in the set.
In S, a 1 in the position corresponding to the location in the set indicates the presence of the
element. So {x, y} = 110.
For the whole power set of S we get:
- { } = 000 (Binary) = 0 (Decimal)
- {x} = 100 = 4
- {y} = 010 = 2
- {z} = 001 = 1
- {x, y} = 110 = 6
- {x, z} = 101 = 5
- {y, z} = 011 = 3
- {x, y, z} = 111 = 7
Relation to binomial theorem
The power set is closely related to the binomial theoremBinomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. The number of sets with
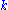 elements in the power set of a set with
elements in the power set of a set with  elements will be a combination
elements will be a combinationCombination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
 also called a binomial coefficient
also called a binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.
For example the power set of a set with three elements, has:
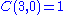 set with 0 elements
set with 0 elements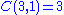 sets with 1 element
sets with 1 element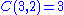 sets with 2 elements
sets with 2 elements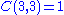 set with 3 elements.
set with 3 elements.
Algorithms
If is a finite set, there is a recursive algorithm to calculate
is a finite set, there is a recursive algorithm to calculate 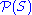 .
.Define the operation
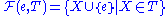
In English, return the set with the element
 added to each set
added to each set 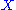 in
in  .
.- If
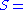 ,then
,then 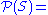 is returned.
is returned. - Otherwise:
- Let
 be any single element of
be any single element of  .
. - Let
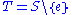 , where '
, where ' ' denotes the relative complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
' denotes the relative complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of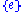 in
in 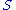 .
. - And the result:
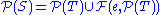 is returned.
is returned.
In other words, the power set of the empty set is the set containing the empty set and the power set of any other set is all the subsets of the set containing some specific element and all the subsets of the set not containing that specific element.
There are other more efficient ways to calculate the power set. For example, use a list of the n elements of S to fix a mapping from the bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
positions of n-bit numbers to those elements; then with a simple loop run through all the 2n numbers representable with n bits, and for each contribute the subset of S corresponding to the bits that are set (to 1) in the number. When n exceeds the word-length of the computer, typically 64 in modern CPUs but greater in modern GPUs, the representation is naturally extended by using an array of words instead of a single word.
Subsets of limited cardinality
The set of subsets of S of cardinality less than κ is denoted by or
or 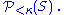 Similarly, the set of non-empty subsets of S might be denoted by
Similarly, the set of non-empty subsets of S might be denoted by 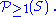
Topologization of power set
Since any family of functions XY from Y to X might be topologized establishing the so-called function spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
, the same can be done with the power set 2S identified as {0,1}S. This particular type of function space is often called a hyperspace and the topology on the power set is referred to as hypertopology.
Power object
A set can be regarded as an algebra having no nontrivial operations or defining equations. From this perspective the idea of the power set of X as the set of subsets of X generalizes naturally to the subalgebras of an algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
or algebra.
Now the power set of a set, when ordered by inclusion, is always a complete atomic Boolean algebra, and every complete atomic Boolean algebra arises as the lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of all subsets of some set. The generalization to arbitrary algebras is that the set of subalgebras of an algebra, again ordered by inclusion, is always an algebraic lattice, and every algebraic lattice arises as the lattice of subalgebras of some algebra. So in that regard subalgebras behave analogously to subsets.
However there are two important properties of subsets that do not carry over to subalgebras in general. First, although the subsets of a set form a set (as well as a lattice), in some classes it may not be possible to organize the subalgebras of an algebra as itself an algebra in that class, although they can always be organized as a lattice. Secondly, whereas the subsets of a set are in bijection with the functions from that set to the set {0,1} = 2, there is no guarantee that a class of algebras contains an algebra that can play the role of 2 in this way.
Certain classes of algebras do enjoy both these properties. The first property is more common, the case of having both is relatively rare. One class that does have both is that of multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
s. Given two multigraphs G and H, a homomorphism h: G → H consists of two functions, one mapping vertices to vertices and the other mapping edges to edges. The set HG of homomorphisms from G to H can then be organized as the graph whose vertices and edges are respectively the vertex and edge functions appearing in that set. Furthermore the subgraphs of a multigraph G are in bijection with the graph homomorphisms from G to the multigraph Ω definable as the complete directed graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on two vertices (hence four edges, namely two self-loops and two more edges forming a cycle) augmented with a fifth edge, namely a second self-loop at one of the vertices. We can therefore organize the subgraphs of G as the multigraph ΩG, called the power object of G.
What is special about a multigraph as an algebra is that its operations are unary. A multigraph has two sorts of elements forming a set V of vertices and E of edges, and has two unary operations s,t: E → V giving the source (start) and target (end) vertices of each edge. An algebra all of whose operations are unary is called a presheaf. Every class of presheaves contains a presheaf Ω that plays the role for subalgebras that 2 plays for subsets. Such a class is a special case of the more general notion of elementary topos
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
as a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
that is closed
Closed category
In category theory, a branch of mathematics, a closed category is a special kind of category.In any category , the morphisms between any two given objects x and y comprise a set, the external hom...
(and moreover cartesian closed
Cartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
) and has an object Ω, called a subobject classifier
Subobject classifier
In category theory, a subobject classifier is a special object Ω of a category; intuitively, the subobjects of an object X correspond to the morphisms from X to Ω. As the name suggests, what a subobject classifier does is to identify/classify subobjects of a given object according to which elements...
. Although the term "power object" is sometimes used synonymously with exponential object
Exponential object
In mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories...
YX, in topos theory Y is required to be Ω.

