
Closed category
Encyclopedia
In category theory
, a branch of mathematics
, a closed category is a special kind of category
.
In any category (more precisely, in any locally small category), the morphisms between any two given objects x and y comprise a set, the external hom (x, y). In a closed category, these morphisms can be seen as comprising an object of the category itself, the internal hom [x,y].
Every closed category has a forgetful functor
to the category of sets
, which in particular takes the internal hom to the external hom.
V with a so called internal Hom functor
 ,
,
left Yoneda arrows natural in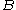 and
and  and dinatural in
and dinatural in 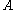
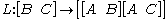
and a fixed object I of V such that there is a natural isomorphism
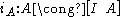
and a dinatural transformation
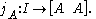
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a closed category is a special kind of category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
In any category (more precisely, in any locally small category), the morphisms between any two given objects x and y comprise a set, the external hom (x, y). In a closed category, these morphisms can be seen as comprising an object of the category itself, the internal hom [x,y].
Every closed category has a forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
to the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, which in particular takes the internal hom to the external hom.
Definition
A closed category can be defined as a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
V with a so called internal Hom functor
Hom functor
In mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.-Formal...
 ,
,left Yoneda arrows natural in
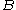 and
and  and dinatural in
and dinatural in 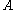
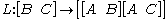
and a fixed object I of V such that there is a natural isomorphism
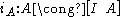
and a dinatural transformation
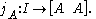
Examples
- Cartesian closed categoriesCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
are closed categories. In particular, any toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
is closed. The canonical example is the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
.
- Compact closed categoriesCompact closed categoryIn category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space...
are closed categories. The canonical example is the categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
FdVect with finite dimensional vector spaces as objects and linear maps as morphisms.
- More generally, any monoidal closed category is a closed category. In this case, the object
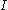 is the monoidal unit.
is the monoidal unit.

