Dinatural transformation
Encyclopedia
In category theory
, a dinatural transformation
between two functor
s
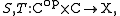
written
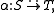
is a function which to every object c of C associates an arrow
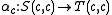of X
and satisfies the following coherence property: for every morphism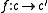
of C the diagram
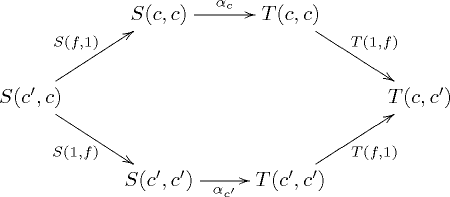
commutes.
The composition of two dinatural transformations need not be dinatural.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a dinatural transformation
between two functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s
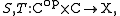
written
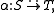
is a function which to every object c of C associates an arrow
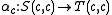of Xand satisfies the following coherence property: for every morphism
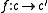of C the diagramcommutes.
The composition of two dinatural transformations need not be dinatural.
External links
- dinatural transformation at the n-Category LabNLabnLab is a wiki-lab of a novel kind, for collaborative work on mathematics, physics, and philosophy, including original research, with a focus on category theory. The nLab espouses the n-point of view : that category theory and higher category theory provide a useful unifying viewpoint for...
.