
Preclosure operator
Encyclopedia
In topology
, a preclosure operator, or Čech closure operator is a map between subsets of a set, similar to a topological closure operator
, except that it is not required to be idempotent. That is, a preclosure operator obeys only three of the four Kuratowski closure axioms
.
 is a map
is a map 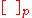
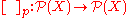
where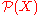 is the power set of
is the power set of  .
.
The preclosure operator has to satisfy the following properties:
The last axiom implies the following:
 is closed (with respect to the preclosure) if
is closed (with respect to the preclosure) if 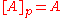 . A set
. A set  is open (with respect to the preclosure) if
is open (with respect to the preclosure) if 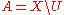 is closed. The collection of all open sets generated by the preclosure operator is a topology
is closed. The collection of all open sets generated by the preclosure operator is a topology
.
The closure operator
cl on this topological space satisfies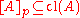 for all
for all  .
.
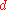 a premetric on
a premetric on  , then
, then
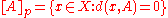
is a preclosure on .
.
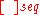 is a preclosure operator. Given a topology
is a preclosure operator. Given a topology  with respect to which the sequential closure operator is defined, the topological space
with respect to which the sequential closure operator is defined, the topological space 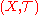 is a sequential space
is a sequential space
if and only if the topology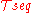 generated by
generated by 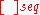 is equal to
is equal to  , that is, if
, that is, if 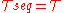 .
.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a preclosure operator, or Čech closure operator is a map between subsets of a set, similar to a topological closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
, except that it is not required to be idempotent. That is, a preclosure operator obeys only three of the four Kuratowski closure axioms
Kuratowski closure axioms
In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
.
Definition
A preclosure operator on a set is a map
is a map 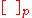
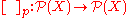
where
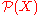 is the power set of
is the power set of  .
.The preclosure operator has to satisfy the following properties:
-
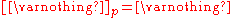 (Preservation of nullary unions);
(Preservation of nullary unions); -
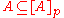 (Extensivity);
(Extensivity); -
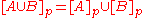 (Preservation of binary unions).
(Preservation of binary unions).
The last axiom implies the following:
- 4.
 implies
implies 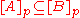 .
.
Topology
A set is closed (with respect to the preclosure) if
is closed (with respect to the preclosure) if 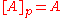 . A set
. A set  is open (with respect to the preclosure) if
is open (with respect to the preclosure) if 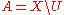 is closed. The collection of all open sets generated by the preclosure operator is a topology
is closed. The collection of all open sets generated by the preclosure operator is a topologyTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.
The closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
cl on this topological space satisfies
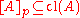 for all
for all  .
.Premetrics
Given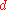 a premetric on
a premetric on  , then
, then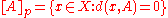
is a preclosure on
 .
.Sequential spaces
The sequential closure operator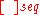 is a preclosure operator. Given a topology
is a preclosure operator. Given a topology  with respect to which the sequential closure operator is defined, the topological space
with respect to which the sequential closure operator is defined, the topological space 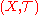 is a sequential space
is a sequential spaceSequential space
In topology and related fields of mathematics, a sequential space is a topological space that satisfies a very weak axiom of countability. Sequential spaces are the most general class of spaces for which sequences suffice to determine the topology....
if and only if the topology
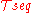 generated by
generated by 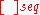 is equal to
is equal to  , that is, if
, that is, if 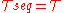 .
.

