Spectrum of a ring
Encyclopedia
In abstract algebra
and algebraic geometry
, the spectrum of a commutative ring
R, denoted by Spec(R), is the set of all proper prime ideal
s of R. It is commonly augmented with the Zariski topology
and with a structure sheaf
, turning it into a locally ringed space.
as follows: a subset V of Spec(R) is closed if and only if there exists an ideal I of R such that V consists of all those prime ideals in R that contain I. This is called the Zariski topology
on Spec(R).
Spec(R) is a compact space
, but almost never Hausdorff
: in fact, the maximal ideal
s in R are precisely the closed points in this topology. However, Spec(R) is always a Kolmogorov space
. It is also a spectral space
.
of R at the multiplicative system {1,f,f2,f3,...}. It can be shown that this satisfies the necessary axioms to be a B-Sheaf. Next, if U is the union of {Dfi}i∈I, we let Γ(U,OX) = limi∈I Rfi, and this produces a sheaf; see the sheaf article for more detail.
If R is an integral domain, with field of fractions K, then we can describe the ring Γ(U,OX) more concretely as follows. We say that an element f in K is regular at a point P in X if it can be represented as a fraction f = a/b with b not in P. Note that this agrees with the notion of a regular function
in algebraic geometry. Using this definition, we can describe Γ(U,OX) as precisely the set of elements of K which are regular at every point P in U.
If P is a point in Spec(R), that is, a prime ideal, then the stalk at P equals the localization
of R at P, and this is a local ring
. Consequently, Spec(R) is a locally ringed space.
Every locally ringed space isomorphic to one of this form is called an affine scheme.
General schemes
are obtained by "gluing together" several affine schemes.
and observe that Spec is a functor
.
Every ring homomorphism
f : R → S induces a continuous map Spec(f) : Spec(S) → Spec(R) (since the preimage of any prime ideal in S is a prime ideal in R). In this way, Spec can be seen as a contravariant functor from the category of commutative rings to the category of topological spaces. Moreover for every prime P the homomorphism f descends to homomorphisms
of local rings. Thus Spec even defines a contravariant functor from the category of commutative rings to the category of locally ringed spaces. In fact it is the universal such functor and this can be used to define the functor Spec up to natural isomorphism.
The functor Spec yields a contravariant equivalence between the category of commutative rings and the category of affine schemes; each of these categories is often thought of as the opposite category
of the other.
one studies algebraic sets, i.e. subsets of Kn (where K is an algebraically closed field
) which are defined as the common zeros of a set of polynomial
s in n variables. If A is such an algebraic set, one considers the commutative ring R of all polynomial functions A → K. The maximal ideals of R correspond to the points of A (because K is algebraically closed), and the prime ideals of R correspond to the subvarieties of A (an algebraic set is called irreducible
or a variety if it cannot be written as the union of two proper algebraic subsets).
The spectrum of R therefore consists of the points of A together with elements for all subvarieties of A. The points of A are closed in the spectrum, while the elements corresponding to subvarieties have a closure consisting of all their points and subvarieties. If one only considers the points of A, i.e. the maximal ideals in R, then the Zariski topology defined above coincides with the Zariski topology defined on algebraic sets (which has precisely the algebraic subsets as closed sets).
One can thus view the topological space Spec(R) as an "enrichment" of the topological space A (with Zariski topology): for every subvariety of A, one additional non-closed point has been introduced, and this point "keeps track" of the corresponding subvariety. One thinks of this point as the generic point
for the subvariety. Furthermore, the sheaf on Spec(R) and the sheaf of polynomial functions on A are essentially identical. By studying spectra of polynomial rings instead of algebraic sets with Zariski topology, one can generalize the concepts of algebraic geometry to non-algebraically closed fields and beyond, eventually arriving at the language of scheme
s.
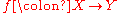such that for every open affine 
, there is an isomorphism induced by f: 
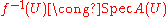, and such that for an inclusion of open affines 
, the inclusion 
induces the restriction map 
, a prime ideal I corresponds to a module R/I, and the spectrum of a ring corresponds to irreducible cyclic representations of R, while more general subvarieties correspond to possibly reducible representations that need not be cyclic. Recall that abstractly, the representation theory of a group is the study of modules over its group algebra
.
The connection to representation theory is clearer if one considers the polynomial ring
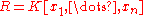or, without a basis, 
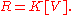As the latter formulation makes clear, a polynomial ring is the group algebra over a vector space
, and writing in terms of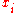
corresponds to choosing a basis for the vector space. Then an ideal I, or equivalently a module 
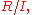is a cyclic representation of R (cyclic meaning generated by 1 element as an R-module; this generalizes 1-dimensional representations).
In the case that the field is closed (say, the complex numbers) and one uses a maximal ideal, which corresponds (by the nullstellensatz) to a point in n-space (the maximal ideal generated by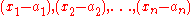
corresponds to the point 
), these representations are parametrized by the dual space 
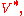(the covector is given by the 
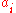). This is precisely Fourier theory: the representations the additive group 
are given by the dual group
(simply, maps
are multiplication by a scalar), and thus the representations of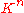 
(K-linear maps 
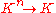) are given by a set of n-numbers, or equivalently a covector 
Thus, points in n-space, thought of as the max spec of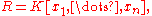
correspond precisely to 1-dimensional representations of R, while finite sets of points correspond to finite-dimensional representations (which are reducible, corresponding geometrically to being a union, and algebraically to not being a prime ideal). The non-maximal ideals then correspond to infinite-dimensional representations.
.
Given a linear operator T on a finite-dimensional vector space V, one can consider the vector space with operator as a module over the polynomial ring in one variable R=K[T], as in the structure theorem for finitely generated modules over a principal ideal domain
. Then the spectrum of K[T] (as a ring) equals the spectrum of T (as an operator).
Further, the geometric structure of the spectrum of the ring (equivalently, the algebraic structure of the module) captures the behavior of the spectrum of the operator, such as algebraic multiplicity and geometric multiplicity. For instance, for the 2×2 identity matrix has corresponding module:
the 2×2 zero matrix has module
showing geometric multiplicity 2 for the zero eigenvalue,
while a non-trivial 2×2 nilpotent matrix has module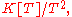
showing algebraic multiplicity 2 but geometric multiplicity 1.
In more detail:
, yielding the notion of the spectrum of a C*-algebra. Notably, for a Hausdorff space
, the algebra of scalars (the bounded continuous functions on the space, being analogous to regular functions) are a commutative C*-algebra, with the space being recovered as a topological space from MSpec of the algebra of scalars, indeed functorially so; this is the content of the Banach–Stone theorem. Indeed, any commutative C*-algebra can be realized as the algebra of scalars of a Hausdorff space in this way, yielding the same correspondence as between a ring and its spectrum. Generalizing to non-commutative C*-algebras yields noncommutative topology
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the spectrum of a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R, denoted by Spec(R), is the set of all proper prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s of R. It is commonly augmented with the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
and with a structure sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
, turning it into a locally ringed space.
Zariski topology
Spec(R) can be turned into a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
as follows: a subset V of Spec(R) is closed if and only if there exists an ideal I of R such that V consists of all those prime ideals in R that contain I. This is called the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
on Spec(R).
Spec(R) is a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, but almost never Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
: in fact, the maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s in R are precisely the closed points in this topology. However, Spec(R) is always a Kolmogorov space
Kolmogorov space
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
. It is also a spectral space
Spectral space
In mathematics, a spectral space is a topological space which is homeomorphic to the spectrum of a commutative ring.-Definition:Let X be a topological space and let K\circ be the set of allquasi-compact and open subsets of X...
.
Sheaves and schemes
To define a structure sheaf on Spec(R), first let Df be the set of all prime ideals P in Spec(R) such that f is not in P. The sets {Df}f∈R form a basis for the topology on Spec(R). Define a sheaf OX on the Df by setting Γ(Df, OX) = Rf, the localizationLocalization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of R at the multiplicative system {1,f,f2,f3,...}. It can be shown that this satisfies the necessary axioms to be a B-Sheaf. Next, if U is the union of {Dfi}i∈I, we let Γ(U,OX) = limi∈I Rfi, and this produces a sheaf; see the sheaf article for more detail.
If R is an integral domain, with field of fractions K, then we can describe the ring Γ(U,OX) more concretely as follows. We say that an element f in K is regular at a point P in X if it can be represented as a fraction f = a/b with b not in P. Note that this agrees with the notion of a regular function
Regular function
In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
in algebraic geometry. Using this definition, we can describe Γ(U,OX) as precisely the set of elements of K which are regular at every point P in U.
If P is a point in Spec(R), that is, a prime ideal, then the stalk at P equals the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of R at P, and this is a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
. Consequently, Spec(R) is a locally ringed space.
Every locally ringed space isomorphic to one of this form is called an affine scheme.
General schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
are obtained by "gluing together" several affine schemes.
Functoriality
It is useful to use the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
and observe that Spec is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
.
Every ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
f : R → S induces a continuous map Spec(f) : Spec(S) → Spec(R) (since the preimage of any prime ideal in S is a prime ideal in R). In this way, Spec can be seen as a contravariant functor from the category of commutative rings to the category of topological spaces. Moreover for every prime P the homomorphism f descends to homomorphisms
- Of -1(P) → OP,
of local rings. Thus Spec even defines a contravariant functor from the category of commutative rings to the category of locally ringed spaces. In fact it is the universal such functor and this can be used to define the functor Spec up to natural isomorphism.
The functor Spec yields a contravariant equivalence between the category of commutative rings and the category of affine schemes; each of these categories is often thought of as the opposite category
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
of the other.
Motivation from algebraic geometry
Following on from the example, in algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
one studies algebraic sets, i.e. subsets of Kn (where K is an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
) which are defined as the common zeros of a set of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in n variables. If A is such an algebraic set, one considers the commutative ring R of all polynomial functions A → K. The maximal ideals of R correspond to the points of A (because K is algebraically closed), and the prime ideals of R correspond to the subvarieties of A (an algebraic set is called irreducible
Irreducible component
In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
or a variety if it cannot be written as the union of two proper algebraic subsets).
The spectrum of R therefore consists of the points of A together with elements for all subvarieties of A. The points of A are closed in the spectrum, while the elements corresponding to subvarieties have a closure consisting of all their points and subvarieties. If one only considers the points of A, i.e. the maximal ideals in R, then the Zariski topology defined above coincides with the Zariski topology defined on algebraic sets (which has precisely the algebraic subsets as closed sets).
One can thus view the topological space Spec(R) as an "enrichment" of the topological space A (with Zariski topology): for every subvariety of A, one additional non-closed point has been introduced, and this point "keeps track" of the corresponding subvariety. One thinks of this point as the generic point
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
for the subvariety. Furthermore, the sheaf on Spec(R) and the sheaf of polynomial functions on A are essentially identical. By studying spectra of polynomial rings instead of algebraic sets with Zariski topology, one can generalize the concepts of algebraic geometry to non-algebraically closed fields and beyond, eventually arriving at the language of scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s.
Global Spec
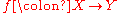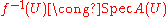There is a relative version of the functor Spec called global Spec, or relative Spec, and denoted by Spec. For a scheme Y, and a quasi-coherent sheaf of OY-algebras A, there is a unique scheme X, called Spec A, and a morphism such that for every open affine , there is an isomorphism induced by f: , and such that for an inclusion of open affines , the inclusion induces the restriction map Representation theory perspective
From the perspective of representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, a prime ideal I corresponds to a module R/I, and the spectrum of a ring corresponds to irreducible cyclic representations of R, while more general subvarieties correspond to possibly reducible representations that need not be cyclic. Recall that abstractly, the representation theory of a group is the study of modules over its group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
.
The connection to representation theory is clearer if one considers the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
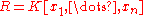or, without a basis, 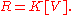As the latter formulation makes clear, a polynomial ring is the group algebra over a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, and writing in terms of
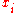corresponds to choosing a basis for the vector space. Then an ideal I, or equivalently a module 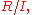is a cyclic representation of R (cyclic meaning generated by 1 element as an R-module; this generalizes 1-dimensional representations).In the case that the field is closed (say, the complex numbers) and one uses a maximal ideal, which corresponds (by the nullstellensatz) to a point in n-space (the maximal ideal generated by
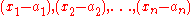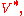corresponds to the point ), these representations are parametrized by the dual space (the covector is given by the 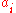). This is precisely Fourier theory: the representations the additive group are given by the dual groupDual group
In mathematics, the dual group may be:* The Pontryagin dual of a locally compact abelian group* The Langlands dual of a reductive algebraic group* The Deligne-Lusztig dual of a reductive group over a finite field....
(simply, maps
are multiplication by a scalar), and thus the representations of 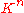(K-linear maps 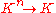) are given by a set of n-numbers, or equivalently a covector Thus, points in n-space, thought of as the max spec of
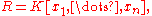correspond precisely to 1-dimensional representations of R, while finite sets of points correspond to finite-dimensional representations (which are reducible, corresponding geometrically to being a union, and algebraically to not being a prime ideal). The non-maximal ideals then correspond to infinite-dimensional representations.Functional analysis perspective
The term "spectrum" comes from the use in operator theoryOperator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
.
Given a linear operator T on a finite-dimensional vector space V, one can consider the vector space with operator as a module over the polynomial ring in one variable R=K[T], as in the structure theorem for finitely generated modules over a principal ideal domain
Structure theorem for finitely generated modules over a principal ideal domain
In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
. Then the spectrum of K[T] (as a ring) equals the spectrum of T (as an operator).
Further, the geometric structure of the spectrum of the ring (equivalently, the algebraic structure of the module) captures the behavior of the spectrum of the operator, such as algebraic multiplicity and geometric multiplicity. For instance, for the 2×2 identity matrix has corresponding module:
the 2×2 zero matrix has module
showing geometric multiplicity 2 for the zero eigenvalue,
while a non-trivial 2×2 nilpotent matrix has module
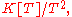
showing algebraic multiplicity 2 but geometric multiplicity 1.
In more detail:
- the eigenvalues (with geometric multiplicity) of the operator correspond to the (reduced) points of the variety, with multiplicity;
- the primary decomposition of the module corresponds to the unreduced points of the variety;
- a diagonalizable (semisimple) operator corresponds to a reduced variety;
- a cyclic module (one generator) corresponds to the operator having a cyclic vector (a vector whose orbit under T spans the space);
- the first invariant factorInvariant factorThe invariant factors of a module over a principal ideal domain occur in one form of the structure theorem for finitely generated modules over a principal ideal domain.If R is a PID and M a finitely generated R-module, then...
of the module equals the minimal polynomialMinimal polynomial (linear algebra)In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
of the operator, and the last invariant factor equals the characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
.
Generalizations
The spectrum can be generalized from rings to C*-algebras in operator theoryOperator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, yielding the notion of the spectrum of a C*-algebra. Notably, for a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, the algebra of scalars (the bounded continuous functions on the space, being analogous to regular functions) are a commutative C*-algebra, with the space being recovered as a topological space from MSpec of the algebra of scalars, indeed functorially so; this is the content of the Banach–Stone theorem. Indeed, any commutative C*-algebra can be realized as the algebra of scalars of a Hausdorff space in this way, yielding the same correspondence as between a ring and its spectrum. Generalizing to non-commutative C*-algebras yields noncommutative topology
Noncommutative topology
Noncommutative topology in mathematics is a term applied to the strictly C*-algebraic part of the noncommutative geometry program. The program has its origins in the Gel'fand duality between the topology of locally compact spaces and the algebraic structure of commutative C*-algebras.Several...
.
External links
- Kevin R. Coombes: The Spectrum of a Ring