
Sheaf (mathematics)
Encyclopedia
In mathematics
, a sheaf is a tool for systematically tracking locally defined data attached to the open set
s of a topological space
. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original one. For example, such data can consist of the ring
s of continuous
or smooth
real-valued function
s defined on each open set. Sheaves are by design quite general and abstract objects, and their correct definition is rather technical. They exist in several varieties such as sheaves of sets or sheaves of rings, depending on the type of data assigned to open sets.
There are also map
s (or morphism
s) from one sheaf to another; sheaves (of a specific type, such as sheaves of abelian group
s) with their morphisms on a fixed topological space form a category
. On the other hand, to each continuous map there is associated both a direct image functor
, taking sheaves and their morphisms on the domain
to sheaves and morphisms on the codomain
, and an inverse image functor operating in the opposite direction. These functors, and certain variants of theirs, are essential parts of sheaf theory.
Due to their general nature and versatility, sheaves have several applications in topology and especially in algebraic
and differential geometry. First, several geometric structures such as that of a differentiable manifold
or a scheme
can be expressed in terms of a sheaf of rings on the space. In such contexts several geometric constructions such as vector bundles or divisors
are naturally specified in terms of sheaves. Second, sheaves provide the framework for a very general cohomology theory
, which encompasses also the "usual" topological cohomology theories such as singular cohomology. Especially in algebraic geometry and the theory of complex manifold
s, sheaf cohomology provides a powerful link between topological and geometric properties of spaces. Sheaves also provide the basis for the theory of D-module
s, which provide applications to the theory of differential equations. In addition, generalizations of sheaves to more general settings
than topological spaces have provided applications to mathematical logic
and number theory
.
, differential geometry and algebraic geometry
, several structures defined on a topological space
(e.g., a differentiable manifold
) can be naturally localised or restricted to open
subset
s of the space: typical examples include continuous
real or complex
-valued functions, n times differentiable
(real or complex-valued) functions, bounded
real-valued functions, vector field
s, and section
s of any vector bundle
on the space.
Presheaves formalise the situation common to the examples above: a presheaf (of sets) on a topological space is a structure that associates to each open set U of the space a set F(U) of "sections" on U, and to each open set V included in U a map F(U) → F(V) giving restrictions of sections over U to V. Each of the examples above defines a presheaf with restrictions of functions, vector fields and sections of a vector bundle having the obvious meaning. Moreover, in each of these examples the sets of sections have additional algebraic structure
: pointwise operations make them abelian group
s, and in the examples of real and complex-valued functions the sets of sections have even a ring
structure. In addition, in each example the restriction maps are homomorphism
s of the corresponding algebraic structure. This observation leads to the natural definition of presheaves with additional algebraic structure such as presheaves of groups, of abelian groups, of rings: section sets are required to have the specified algebraic structure, and the restrictions are required to be homomorphisms. Thus for example continuous real-valued functions on a topological space form a presheaf of rings on the space.
Given a presheaf, a natural question to ask is to what extent its sections over an open set U are specified by their restrictions to smaller open sets Vi of an open cover of U. A presheaf is separated if its sections are "locally determined": whenever two sections over U coincide when restricted to each of Vi, the two sections are identical. All examples of presheaves discussed above are separated, since in each case the sections are specified by their values at the points of the underlying space. Finally, a separated presheaf is a sheaf if compatible sections can be glued together, i.e., whenever there is a section of the presheaf over each of the covering sets Vi, chosen so that they match on the overlaps of the covering sets, these sections correspond to a (unique) section on U, of which they are restrictions. It is easy to verify that all examples above except the presheaf of bounded functions are in fact sheaves: in all cases the criterion of being a section of the presheaf is local in a sense that it is enough to verify it in an arbitrary neighbourhood of each point.
On the other hand, it is clear that a function can be bounded on each set of an (infinite) open cover of a space without being bounded on all of the space; thus bounded functions provide an example of a presheaf that in general fails to be a sheaf. Another example of a presheaf that fails to be a sheaf is the constant presheaf that associates the same fixed set (or abelian group, or a ring,...) to each open set: it follows from the gluing property of sheaves that sections on a disjoint union of two open sets is the Cartesian product
of the sections over the two open sets. The correct way to define the constant sheaf
FA (associated to for instance a set A) on a topological space is to require sections on an open set U to be continuous maps from U to A equipped with the discrete topology; then in particular FA(U) = A for connected
U.
Maps between presheaves and sheaves (called morphism
s) consist of maps between the sets of sections over each open set of the underlying space, compatible with restrictions of sections. If the presheaves or sheaves considered are provided with additional algebraic structure, these maps are assumed to be homomorphisms. Sheaves endowed with nontrivial endomorphisms, such as the action of an algebraic torus
or a Galois group
, are of particular interest.
Presheaves and sheaves are typically denoted by capital letters, F being particularly common, presumably for the French
word for sheaves, faisceau. Use of script letters such as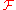 is also common.
is also common.
, the category of groups
, the category of abelian groups
, or the category of commutative rings. A presheaf F on X with values in C is given by the following data:
The morphisms resV,U are called restriction morphisms. The restriction morphisms are required to satisfy two properties.
Informally, the second axiom says it doesn't matter whether we restrict to W in one step or restrict first to V, then to W.
There is a compact way to express the notion of a presheaf in terms of category theory
. First we define the category
of open sets on X to be the category O(X) whose objects are the open sets of X and whose morphisms are inclusions. Then a C-valued presheaf on X is the same as a contravariant functor from O(X) to C. This definition can be generalized to the case when the source category is not of the form O(X) for any X; see presheaf (category theory).
If F is a C-valued presheaf on X, and U is an open subset of X, then F(U) is called the sections of F over U. If C is a concrete category
, then each element of F(U) is called a section. A section over X is called a global section. A common notation (used also below) for the restriction resV,U(s) of a section is s|V. This terminology and notation is by analogy with sections of fiber bundle
s or sections of the étalé space of a sheaf; see below. F(U) is also often denoted Γ(U,F), especially in contexts such as sheaf cohomology
where U tends to be fixed and F tends to be variable.
whose underlying set functor is conservative, meaning that if the underlying map of sets is a bijection, then the original morphism is an isomorphism.
A sheaf is a presheaf with values in the category of sets that satisfies the following two axioms:
of an open set U, and if s,t ∈ F(U) are such that s|Ui = t|Ui for each set Ui of the covering, then s = t; and (Gluing) If ( Ui) is an open covering of an open set U, and if for each i there is a section si of F over Ui such that for each pair Ui,Uj of the covering sets the restrictions of si and sj agree on the overlaps: si|Ui∩Uj = sj|Ui∩Uj, then there is a section s ∈ F(U) such that s|Ui = si for each i.
The section s whose existence is guaranteed by axiom 2 is called the gluing, concatenation, or collation of the sections si. By axiom 1 it is unique. Sections si satisfying the condition of axiom 2 are often called compatible; thus axioms 1 and 2 together state that compatible sections can be uniquely glued together. A separated presheaf, or monopresheaf, is a presheaf satisfying axiom 1.
Assume now that C is a general category but that C has products
. Then the sheaf axioms can be expressed as the exactness of the sequence
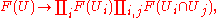
where the first map is the product of the restriction maps
and the pair of arrows the products of the two sets of restrictions
and
A presheaf F is a sheaf precisely when for each open covering of an open set U by a family Ui of open subsets of U, the first arrow in the diagram above is an equalizer. For a separated presheaf, the first arrow need only be injective.
In general, construct a category J whose objects are the sets Ui and the intersections and whose morphisms are the inclusions of in Ui and Uj. The sheaf axiom is that the limit
of the functor F restricted to the category J must be isomorphic to F(U).
Notice that the empty subset of a topological space is covered by the empty family of sets. The product of an empty family or the limit of an empty family is a terminal object, and consequently the value of a sheaf on the empty set must be a terminal object. If sheaf values are in the category of sets, applying the local identity axiom to the empty family shows that over the empty set, there is at most one section, and applying the gluing axiom to the empty family shows that there is at least one section. This property is called normalization axiom.
It can be shown that to specify a sheaf, it is enough to specify its restriction to the open sets of a basis for the topology of the underlying space. Moreover, it can also be shown that it is enough to verify the sheaf axioms above relative to the open sets of a covering. Thus a sheaf can often be defined by giving its values on the open sets of a basis, and verifying the sheaf axioms relative to the basis.
Let F and G be two sheaves on X with values in the category C. A morphism
φ : G → F consists of a morphism φ(U) : G(U) → F(U) for each open set U of X, subject to the condition that this morphism is compatible with restrictions. In other words, for every open subset V of an open set U, the following diagram
is commutative
.
Recall that we could also express a sheaf as a special kind of functor. In this language, a morphism of sheaves is a natural transformation
of the corresponding functors. With this notion of morphism, there is a category of C-valued sheaves on X for any C. The objects are the C-valued sheaves, and the morphisms are morphisms of sheaves. An isomorphism
of sheaves is an isomorphism in this category.
It can be proved that an isomorphism of sheaves is an isomorphism on each open set U. In other words, φ is an isomorphism if and only if for each U, φ(U) is an isomorphism. The same is true of monomorphism
s, but not of epimorphism
s. See sheaf cohomology
.
Notice that we did not use the gluing axiom in defining a morphism of sheaves. Consequently, the above definition makes sense for presheaves as well. The category of C-valued presheaves is then a functor category
, the category of contravariant functors from O(X) to C.
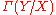 on X by setting
on X by setting 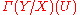 equal to the sections U → Y, that is,
equal to the sections U → Y, that is, 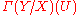 is the set of all functions s : U → Y such that fs = idU. Restriction is given by restriction of functions. This sheaf is called the sheaf of sections of f, and it is especially important when f is the projection of a fiber bundle
is the set of all functions s : U → Y such that fs = idU. Restriction is given by restriction of functions. This sheaf is called the sheaf of sections of f, and it is especially important when f is the projection of a fiber bundle
onto its base space. Notice that if the image of f does not contain U, then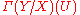 is empty. For a concrete example, take
is empty. For a concrete example, take  ,
,  , and
, and 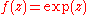 .
. 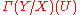 is the set of branches of the logarithm on
is the set of branches of the logarithm on  .
.
Fix a point x in X and an object S in a category C. The skyscraper sheaf over x with stalk S is the sheaf Sx defined as follows: If U is an open set containing x, then Sx(U) = S. If U does not contain x, then Sx(U) is the terminal object of C. The restriction maps are either the identity on S, if both open sets contain x, or the unique map from S to the terminal object of C.
 such that
such that 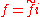 . In fact a is the adjoint functor to the inclusion functor from the category of sheaves to the category of presheaves, and i is the unit of the adjunction.
. In fact a is the adjoint functor to the inclusion functor from the category of sheaves to the category of presheaves, and i is the unit of the adjunction.
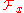 of a sheaf
of a sheaf 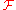 captures the properties of a sheaf "around" a point x ∈ X.
captures the properties of a sheaf "around" a point x ∈ X.
Here, "around" means that, conceptually speaking, one looks at smaller and smaller neighborhood of the point. Of course, no single neighborhood will be small enough, so we will have to take a limit of some sort.
The stalk is defined by
the direct limit
being over all open subsets of X containing the given point x. In other words, an element of the stalk is given by a section over some open neighborhood of x, and two such sections are considered equivalent if their restrictions agree on a smaller neighborhood.
The natural morphism F(U) → Fx takes a section s in F(U) to its germ. This generalises the usual definition of a germ
.
A different way of defining the stalk is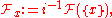
where i is the inclusion of the one-point space {x} into X. The equivalence follows from the definition of the inverse image
.
In many situations, knowing the stalks of a sheaf is enough to control the sheaf itself. For example, whether or not a morphism of sheaves is a monomorphism, epimorphism, or isomorphism can be tested on the stalks. They also find use in constructions such as Godement resolution
s.
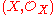 consisting of a topological space X and a sheaf of rings on X is called a ringed space
consisting of a topological space X and a sheaf of rings on X is called a ringed space
. Many types of spaces can be defined as certain types of ringed spaces. The sheaf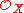 is called the structure sheaf of the space. A very common situation is when all the stalks of the structure sheaf are local ring
is called the structure sheaf of the space. A very common situation is when all the stalks of the structure sheaf are local ring
s, in which case the pair is called a locally ringed space. Here are examples of definitions made in this way:
 be a ringed space. A sheaf of modules is a sheaf
be a ringed space. A sheaf of modules is a sheaf 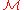 such that on every open set U of X,
such that on every open set U of X,  is an
is an 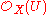 -module and for every inclusion of open sets V ⊆ U, the restriction map
-module and for every inclusion of open sets V ⊆ U, the restriction map  is a homomorphism of
is a homomorphism of 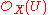 -modules.
-modules.
Most important geometric objects are sheaves of modules. For example, there is a one-to-one correspondence between vector bundle
s and locally free sheaves of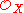 -modules. Sheaves of solutions to differential equations are D-module
-modules. Sheaves of solutions to differential equations are D-module
s, that is, modules over the sheaf of differential operators.
A particularly important case are abelian sheaves, which are modules over the constant sheaf . Every sheaf of modules is an abelian sheaf.
. Every sheaf of modules is an abelian sheaf.
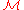 is finitely generated if, for every point x of X, there exists an open neighborhood U of x, a natural number n (possibly depending on U), and a surjective morphism of sheaves
is finitely generated if, for every point x of X, there exists an open neighborhood U of x, a natural number n (possibly depending on U), and a surjective morphism of sheaves 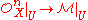 . Similarly,
. Similarly, 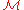 is finitely presented if in addition there exists a natural number m (again possibly depending on U) and a morphism of sheaves
is finitely presented if in addition there exists a natural number m (again possibly depending on U) and a morphism of sheaves  such that the sequence of morphisms
such that the sequence of morphisms  is exact. Equivalently, the kernel of the morphism
is exact. Equivalently, the kernel of the morphism 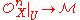 is itself a finitely generated sheaf.
is itself a finitely generated sheaf.
These, however, are not the only possible finiteness conditions on a sheaf. The most important finiteness condition for a sheaf is coherence. is coherent if it is of finite type and if, for every open set U and every morphism of sheaves
is coherent if it is of finite type and if, for every open set U and every morphism of sheaves 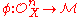 (not necessarily surjective), the kernel of φ is of finite type.
(not necessarily surjective), the kernel of φ is of finite type.  is coherent if it is coherent as a module over itself. Note that coherence is a strictly stronger condition than finite presentation:
is coherent if it is coherent as a module over itself. Note that coherence is a strictly stronger condition than finite presentation: 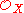 is always finitely presented as a module over itself, but it is not always coherent. For example, let X be a point, let
is always finitely presented as a module over itself, but it is not always coherent. For example, let X be a point, let  be the ring R = C[x1, x2, ...] of complex polynomials in countably many indeterminates. Choose n = 1, and for the morphism φ, take the map that sends every variable to zero. The kernel of this map is not finitely generated, so
be the ring R = C[x1, x2, ...] of complex polynomials in countably many indeterminates. Choose n = 1, and for the morphism φ, take the map that sends every variable to zero. The kernel of this map is not finitely generated, so 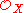 is not coherent.
is not coherent.
π: E → X such that the sheaf of sections of π is F. E is usually a very strange space, and even if the sheaf F arises from a natural topological situation, E may not have any clear topological interpretation. For example, if F is the sheaf of sections of a continuous function f : Y → X, then E = Y if and only if f is a local homeomorphism
.
The étalé space E is constructed from the stalks of F over X. As a set, it is their disjoint union
and π is the obvious map that takes the value x on the stalk of F over x ∈ X. The topology of E is defined as follows. For each element s of F(U) and each x in U, we get a germ of s at x. These germs determine points of E. For any U and s ∈ F(U), the union of these points (for all x ∈ U) is declared to be open in E. Notice that each stalk has the discrete topology as subspace topology. Two morphisms between sheaves determine a continuous map of the corresponding étalé spaces that is compatible with the projection maps (in the sense that every germ is mapped to a germ over the same point). This makes the construction into a functor.
The construction above determines an equivalence of categories
between the category of sheaves of sets on X and the category of étalé spaces over X. The construction of an étalé space can also be applied to a presheaf, in which case the sheaf of sections of the étalé space recovers the sheaf associated to the given presheaf.
This construction makes all sheaves into representable functor
s on certain categories of topological spaces. As above, let F be a sheaf on X, let E be its étalé space, and let π: E → X be the natural projection. Consider the category Top/X of topological spaces over X, that is, the category of topological spaces together with fixed continuous maps to X. Every object of this space is a continuous map f : Y → X, and a morphism from Y → X to Z → X is a continuous map Y → Z that commutes with the two maps to X. There is a functor Γ from Top/X to the category of sets which takes an object f : Y → X to (f−1F)(Y). For example, if i : U → X is the inclusion of an open subset, then Γ(i) = (i−1F)(U) agrees with the usual F(U), and if i : {x} → X is the inclusion of a point, then Γ({x}) = (i−1F)({x}) is the stalk of F at x. There is a natural isomorphism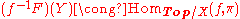
which shows that E represents the functor Γ.
E is constructed so that the projection map π is a covering map. In algebraic geometry, the natural analog of a covering map is called an étale morphism
. Despite its similarity to "étalé", the word étale etal has a different meaning both in French and in mathematics. In particular, it is possible to turn E into a scheme
and π into a morphism of schemes in such a way that π retains the same universal property, but π is not in general an étale morphism because it is not quasi-finite. It is, however, formally étale.
The definition of sheaves by étalé spaces is older than the definition given earlier in the article. It is still common in some areas of mathematics such as mathematical analysis
.
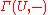 preserves isomorphisms and monomorphisms, but not epimorphisms. If F is a sheaf of abelian groups, or more generally a sheaf with values in an abelian category
preserves isomorphisms and monomorphisms, but not epimorphisms. If F is a sheaf of abelian groups, or more generally a sheaf with values in an abelian category
, then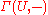 is actually a left exact functor. This means that it is possible to construct derived functor
is actually a left exact functor. This means that it is possible to construct derived functor
s of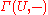 . These derived functors are called the cohomology groups (or modules) of F and are written
. These derived functors are called the cohomology groups (or modules) of F and are written 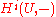 . Grothendieck proved in his Tohoku paper that every category of sheaves of abelian groups contains enough injective object
. Grothendieck proved in his Tohoku paper that every category of sheaves of abelian groups contains enough injective object
s, so these derived functors always exist.
However, computing sheaf cohomology using injective resolutions is nearly impossible. In practice, it is much more common to find a different and more tractable resolution of F. A general construction is provided by Godement resolution
s, and particular resolutions may be constructed using soft sheaves, fine sheaves, and flabby sheaves (also known as flasque sheaves from the French flasque meaning flabby). As a consequence, it can become possible to compare sheaf cohomology with other cohomology theories. For example, the de Rham complex is a resolution of the constant sheaf on any smooth manifold, so the sheaf cohomology of
on any smooth manifold, so the sheaf cohomology of  is equal to its de Rham cohomology
is equal to its de Rham cohomology
. In fact, comparing sheaf cohomology to de Rham cohomology and singular cohomology provides a proof of de Rham's theorem that the two cohomology theories are isomorphic.
A different approach is by Čech cohomology
. Čech cohomology was the first cohomology theory developed for sheaves and it is well-suited to concrete calculations. It relates sections on open subsets of the space to cohomology classes on the space. In most cases, Čech cohomology computes the same cohomology groups as the derived functor cohomology. However, for some pathological spaces, Čech cohomology will give the correct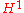 but incorrect higher cohomology groups. To get around this, Jean-Louis Verdier
but incorrect higher cohomology groups. To get around this, Jean-Louis Verdier
developed hypercoverings. Hypercoverings not only give the correct higher cohomology groups but also allow the open subsets mentioned above to be replaced by certain morphisms from another space. This flexibility is necessary in some applications, such as the construction of Pierre Deligne
's mixed Hodge structures.
A much cleaner approach to the computation of some cohomology groups is the Borel–Bott–Weil theorem
, which identifies the cohomology groups of some line bundle
s on flag manifold
s with irreducible representations of Lie group
s. This theorem can be used, for example, to easily compute the cohomology groups of all line bundles on projective space.
In many cases there is a duality theory for sheaves that generalizes Poincaré duality
. See Grothendieck duality and Verdier duality
.
's Weil conjectures
stated that there was a cohomology theory
for algebraic varieties
over finite field
s that would give an analogue of the Riemann hypothesis
. The only natural topology on such a variety, however, is the Zariski topology
, but sheaf cohomology in the Zariski topology is badly behaved because there are very few open sets. Alexandre Grothendieck solved this problem by introducing Grothendieck topologies
, which axiomatize the notion of covering. Grothendieck's insight was that the definition of a sheaf depends only on the open sets of a topological space, not on the individual points. Once he had axiomatized the notion of covering, open sets could be replaced by other objects. A presheaf takes each one of these objects to data, just as before, and a sheaf is a presheaf that satisfies the gluing axiom with respect to our new notion of covering. This allowed Grothendieck to define étale cohomology
and l-adic cohomology, which eventually were used to prove the Weil conjectures.
A category with a Grothendieck topology is called a site. A category of sheaves on a site is called a topos or a Grothendieck topos. The notion of a topos was later abstracted by William Lawvere
and Miles Tierney to define an elementary topos, which has connections to mathematical logic
.
. It took about 15 years for a recognisable, free-standing theory of sheaves to emerge from the foundational work on cohomology
.
At this point sheaves had become a mainstream part of mathematics, with use by no means restricted to algebraic topology
. It was later discovered that the logic in categories of sheaves is intuitionistic logic
(this observation is now often referred to as Kripke–Joyal semantics, but probably should be attributed to a number of authors). This shows that some of the facets of sheaf theory can also be traced back as far as Leibniz.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a sheaf is a tool for systematically tracking locally defined data attached to the open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original one. For example, such data can consist of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s of continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
or smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
real-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s defined on each open set. Sheaves are by design quite general and abstract objects, and their correct definition is rather technical. They exist in several varieties such as sheaves of sets or sheaves of rings, depending on the type of data assigned to open sets.
There are also map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
s (or morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s) from one sheaf to another; sheaves (of a specific type, such as sheaves of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s) with their morphisms on a fixed topological space form a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
. On the other hand, to each continuous map there is associated both a direct image functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
, taking sheaves and their morphisms on the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
to sheaves and morphisms on the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
, and an inverse image functor operating in the opposite direction. These functors, and certain variants of theirs, are essential parts of sheaf theory.
Due to their general nature and versatility, sheaves have several applications in topology and especially in algebraic
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and differential geometry. First, several geometric structures such as that of a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
or a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
can be expressed in terms of a sheaf of rings on the space. In such contexts several geometric constructions such as vector bundles or divisors
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
are naturally specified in terms of sheaves. Second, sheaves provide the framework for a very general cohomology theory
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
, which encompasses also the "usual" topological cohomology theories such as singular cohomology. Especially in algebraic geometry and the theory of complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s, sheaf cohomology provides a powerful link between topological and geometric properties of spaces. Sheaves also provide the basis for the theory of D-module
D-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
s, which provide applications to the theory of differential equations. In addition, generalizations of sheaves to more general settings
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...
than topological spaces have provided applications to mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
Introduction
In topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, differential geometry and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, several structures defined on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
(e.g., a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
) can be naturally localised or restricted to open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the space: typical examples include continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
real or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued functions, n times differentiable
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
(real or complex-valued) functions, bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
real-valued functions, vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s, and section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
s of any vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
on the space.
Presheaves formalise the situation common to the examples above: a presheaf (of sets) on a topological space is a structure that associates to each open set U of the space a set F(U) of "sections" on U, and to each open set V included in U a map F(U) → F(V) giving restrictions of sections over U to V. Each of the examples above defines a presheaf with restrictions of functions, vector fields and sections of a vector bundle having the obvious meaning. Moreover, in each of these examples the sets of sections have additional algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
: pointwise operations make them abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, and in the examples of real and complex-valued functions the sets of sections have even a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
structure. In addition, in each example the restriction maps are homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s of the corresponding algebraic structure. This observation leads to the natural definition of presheaves with additional algebraic structure such as presheaves of groups, of abelian groups, of rings: section sets are required to have the specified algebraic structure, and the restrictions are required to be homomorphisms. Thus for example continuous real-valued functions on a topological space form a presheaf of rings on the space.
Given a presheaf, a natural question to ask is to what extent its sections over an open set U are specified by their restrictions to smaller open sets Vi of an open cover of U. A presheaf is separated if its sections are "locally determined": whenever two sections over U coincide when restricted to each of Vi, the two sections are identical. All examples of presheaves discussed above are separated, since in each case the sections are specified by their values at the points of the underlying space. Finally, a separated presheaf is a sheaf if compatible sections can be glued together, i.e., whenever there is a section of the presheaf over each of the covering sets Vi, chosen so that they match on the overlaps of the covering sets, these sections correspond to a (unique) section on U, of which they are restrictions. It is easy to verify that all examples above except the presheaf of bounded functions are in fact sheaves: in all cases the criterion of being a section of the presheaf is local in a sense that it is enough to verify it in an arbitrary neighbourhood of each point.
On the other hand, it is clear that a function can be bounded on each set of an (infinite) open cover of a space without being bounded on all of the space; thus bounded functions provide an example of a presheaf that in general fails to be a sheaf. Another example of a presheaf that fails to be a sheaf is the constant presheaf that associates the same fixed set (or abelian group, or a ring,...) to each open set: it follows from the gluing property of sheaves that sections on a disjoint union of two open sets is the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of the sections over the two open sets. The correct way to define the constant sheaf
Constant sheaf
In mathematics, the constant sheaf on a topological space X associated to a set A is a sheaf of sets on X whose stalks are all equal to A. It is denoted by or AX. The constant presheaf with value A is the presheaf that assigns to each open subset of X the value A, and all of whose restriction maps...
FA (associated to for instance a set A) on a topological space is to require sections on an open set U to be continuous maps from U to A equipped with the discrete topology; then in particular FA(U) = A for connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
U.
Maps between presheaves and sheaves (called morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s) consist of maps between the sets of sections over each open set of the underlying space, compatible with restrictions of sections. If the presheaves or sheaves considered are provided with additional algebraic structure, these maps are assumed to be homomorphisms. Sheaves endowed with nontrivial endomorphisms, such as the action of an algebraic torus
Algebraic torus
In mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory...
or a Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
, are of particular interest.
Presheaves and sheaves are typically denoted by capital letters, F being particularly common, presumably for the French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
word for sheaves, faisceau. Use of script letters such as
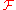 is also common.
is also common.Formal definitions
The first step in defining a sheaf is to define a presheaf, which captures the idea of associating data and restriction maps to the open sets of a topological space. The second step is to require the normalization and gluing axioms. A presheaf that satisfies these axioms is a sheaf.Presheaves
Let X be a topological space, and let C be a category. Usually C is the category of setsCategory of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
, or the category of commutative rings. A presheaf F on X with values in C is given by the following data:
- For each open set U of X, there corresponds an object F(U) in C
- For each inclusion of open sets V ⊆ U, there corresponds a morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
resV,U : F(U) → F(V) in the category C.
The morphisms resV,U are called restriction morphisms. The restriction morphisms are required to satisfy two properties.
- For every open set U of X, the restriction morphism resU,U : F(U) → F(U) is the identity morphism on F(U).
- If we have three open sets W ⊆ V ⊆ U, then the compositeFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
Informally, the second axiom says it doesn't matter whether we restrict to W in one step or restrict first to V, then to W.
There is a compact way to express the notion of a presheaf in terms of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. First we define the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of open sets on X to be the category O(X) whose objects are the open sets of X and whose morphisms are inclusions. Then a C-valued presheaf on X is the same as a contravariant functor from O(X) to C. This definition can be generalized to the case when the source category is not of the form O(X) for any X; see presheaf (category theory).
If F is a C-valued presheaf on X, and U is an open subset of X, then F(U) is called the sections of F over U. If C is a concrete category
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
, then each element of F(U) is called a section. A section over X is called a global section. A common notation (used also below) for the restriction resV,U(s) of a section is s|V. This terminology and notation is by analogy with sections of fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s or sections of the étalé space of a sheaf; see below. F(U) is also often denoted Γ(U,F), especially in contexts such as sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
where U tends to be fixed and F tends to be variable.
Sheaves
For simplicity, consider first the case where the sheaf takes values in the category of sets. In fact, this definition applies more generally to the situation where the category is a concrete categoryConcrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
whose underlying set functor is conservative, meaning that if the underlying map of sets is a bijection, then the original morphism is an isomorphism.
A sheaf is a presheaf with values in the category of sets that satisfies the following two axioms:
- (Local identity) If (
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
of an open set U, and if s,t ∈ F(U) are such that s|Ui = t|Ui for each set Ui of the covering, then s = t; and
The section s whose existence is guaranteed by axiom 2 is called the gluing, concatenation, or collation of the sections si. By axiom 1 it is unique. Sections si satisfying the condition of axiom 2 are often called compatible; thus axioms 1 and 2 together state that compatible sections can be uniquely glued together. A separated presheaf, or monopresheaf, is a presheaf satisfying axiom 1.
Assume now that C is a general category but that C has products
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
. Then the sheaf axioms can be expressed as the exactness of the sequence
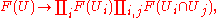
where the first map is the product of the restriction maps
- resUi,U:F(U)→F(Ui)
and the pair of arrows the products of the two sets of restrictions
- resUi∩Uj,Ui:F(Ui)→F(Ui∩Uj)
and
- resUi∩Uj,Uj:F(Uj)→F(Ui∩Uj).
A presheaf F is a sheaf precisely when for each open covering of an open set U by a family Ui of open subsets of U, the first arrow in the diagram above is an equalizer. For a separated presheaf, the first arrow need only be injective.
In general, construct a category J whose objects are the sets Ui and the intersections and whose morphisms are the inclusions of in Ui and Uj. The sheaf axiom is that the limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
of the functor F restricted to the category J must be isomorphic to F(U).
Notice that the empty subset of a topological space is covered by the empty family of sets. The product of an empty family or the limit of an empty family is a terminal object, and consequently the value of a sheaf on the empty set must be a terminal object. If sheaf values are in the category of sets, applying the local identity axiom to the empty family shows that over the empty set, there is at most one section, and applying the gluing axiom to the empty family shows that there is at least one section. This property is called normalization axiom.
It can be shown that to specify a sheaf, it is enough to specify its restriction to the open sets of a basis for the topology of the underlying space. Moreover, it can also be shown that it is enough to verify the sheaf axioms above relative to the open sets of a covering. Thus a sheaf can often be defined by giving its values on the open sets of a basis, and verifying the sheaf axioms relative to the basis.
Morphisms
Heuristically speaking, a morphism of sheaves is analogous to a function between them. However, because sheaves contain data relative to every open set of a topological space, a morphism of sheaves is defined as a collection of functions, one for each open set, that satisfy a compatibility condition.Let F and G be two sheaves on X with values in the category C. A morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
φ : G → F consists of a morphism φ(U) : G(U) → F(U) for each open set U of X, subject to the condition that this morphism is compatible with restrictions. In other words, for every open subset V of an open set U, the following diagram
is commutative
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
.
Recall that we could also express a sheaf as a special kind of functor. In this language, a morphism of sheaves is a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
of the corresponding functors. With this notion of morphism, there is a category of C-valued sheaves on X for any C. The objects are the C-valued sheaves, and the morphisms are morphisms of sheaves. An isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of sheaves is an isomorphism in this category.
It can be proved that an isomorphism of sheaves is an isomorphism on each open set U. In other words, φ is an isomorphism if and only if for each U, φ(U) is an isomorphism. The same is true of monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
s, but not of epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s. See sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
.
Notice that we did not use the gluing axiom in defining a morphism of sheaves. Consequently, the above definition makes sense for presheaves as well. The category of C-valued presheaves is then a functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
, the category of contravariant functors from O(X) to C.
Examples
Because sheaves encode exactly the data needed to pass between local and global situations, there are many examples of sheaves occurring throughout mathematics. Here are some additional examples of sheaves:- Any continuous map of topological spaces determines a sheaf of sets. Let
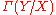 on X by setting
on X by setting 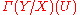 equal to the sections U → Y, that is,
equal to the sections U → Y, that is, 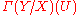 is the set of all functions s : U → Y such that fs = idU. Restriction is given by restriction of functions. This sheaf is called the sheaf of sections of f, and it is especially important when f is the projection of a fiber bundle
is the set of all functions s : U → Y such that fs = idU. Restriction is given by restriction of functions. This sheaf is called the sheaf of sections of f, and it is especially important when f is the projection of a fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
onto its base space. Notice that if the image of f does not contain U, then
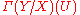 is empty. For a concrete example, take
is empty. For a concrete example, take  ,
,  , and
, and 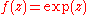 .
. 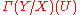 is the set of branches of the logarithm on
is the set of branches of the logarithm on  .
.
Sheaves on manifolds
In the following examples M is an n-dimensional Ck-manifold. The table lists the values of certain sheaves over open subsets U of M and their restriction maps.| Sheaf | Sections over an open set U | Restriction maps | Remarks |
|---|---|---|---|
Sheaf of j-times continuously differentiable functions  , j ≤ k , j ≤ k |
Cj-functions U → R | Restriction of functions. | This is a sheaf of rings with addition and multiplication given by pointwise addition and multiplication. When j = k, this sheaf is called the structure sheaf and is denoted 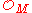 . . |
Sheaf of nonzero k-times continuously differentiable functions  |
Nowhere zero Ck-functions U → R | Restriction of functions. | A sheaf of groups under pointwise multiplication. |
| Cotangent sheaves ΩpM | Differential form Differential form In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus... s of degree p on U |
Restriction of differential forms. | Ω1M and ΩnM are commonly denoted ΩM and ωM, respectively. |
Sheaf of distributions  |
Distribution Distribution (mathematics) In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative... s on U |
The dual map to extension of smooth compactly supported functions by zero. | Here M is assumed to be smooth. |
Sheaf of differential operators 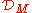 |
Finite-order differential operator Differential operator In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,... s on U |
Restriction of differential operators. | Here M is assumed to be smooth. |
Presheaves that are not sheaves
Here are two examples of presheaves that are not sheaves:- Let X be the two-point topological spaceDiscrete two-point spaceIn topology, a branch of mathematics, a discrete two-point space is the simplest example of a totally disconnected discrete space. The points can be denoted by the symbols 0 and 1....
{x, y} with the discrete topology. Define a presheaf F as follows: F(∅) = {∅}, F({x}) = R, F({y}) = R, F({x, y}) = R × R × R. The restriction map F({x, y}) → F({x}) is the projection of R × R × R onto its first coordinate, and the restriction map F({x, y}) → F({y}) is the projection of R × R × R onto its second coordinate. F is a presheaf that is not separated: A global section is determined by three numbers, but the values of that section over {x} and {y} determine only two of those numbers. So while we can glue any two sections over {x} and {y}, we cannot glue them uniquely. - Let X be the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, and let F(U) be the set of boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
continuous functions on U. This is not a sheaf because it is not always possible to glue. For example, let Ui be the set of all x such that |x| < i. The identity function f(x) = x is bounded on each Ui. Consequently we get a section si on Ui. However, these sections do not glue, because the function f is not bounded on the real line. Consequently F is a presheaf, but not a sheaf. In fact, F is separated because it is a sub-presheaf of the sheaf of continuous functions.
Turning a presheaf into a sheaf
It is frequently useful to take the data contained in a presheaf and to express it as a sheaf. It turns out that there is a best possible way to do this. It takes a presheaf F and produces a new sheaf aF called the sheaving, sheafification or sheaf associated to the presheaf F. a is called the sheaving functor, sheafification functor, or associated sheaf functor. There is a natural morphism of presheaves i : F → aF that has the universal property that for any sheaf G and any morphism of presheaves f : F → G, there is a unique morphism of sheaves such that
such that 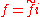 . In fact a is the adjoint functor to the inclusion functor from the category of sheaves to the category of presheaves, and i is the unit of the adjunction.
. In fact a is the adjoint functor to the inclusion functor from the category of sheaves to the category of presheaves, and i is the unit of the adjunction.Stalks of a sheaf
The stalk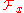 of a sheaf
of a sheaf 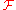 captures the properties of a sheaf "around" a point x ∈ X.
captures the properties of a sheaf "around" a point x ∈ X.Here, "around" means that, conceptually speaking, one looks at smaller and smaller neighborhood of the point. Of course, no single neighborhood will be small enough, so we will have to take a limit of some sort.
The stalk is defined by

the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
being over all open subsets of X containing the given point x. In other words, an element of the stalk is given by a section over some open neighborhood of x, and two such sections are considered equivalent if their restrictions agree on a smaller neighborhood.
The natural morphism F(U) → Fx takes a section s in F(U) to its germ. This generalises the usual definition of a germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
.
A different way of defining the stalk is
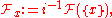
where i is the inclusion of the one-point space {x} into X. The equivalence follows from the definition of the inverse image
Inverse image functor
In mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
.
In many situations, knowing the stalks of a sheaf is enough to control the sheaf itself. For example, whether or not a morphism of sheaves is a monomorphism, epimorphism, or isomorphism can be tested on the stalks. They also find use in constructions such as Godement resolution
Godement resolution
The Godement resolution of a sheaf is a construction in homological algebra which allows one to view global, cohomological information about the sheaf in terms of local information coming from its stalks. It is useful for computing sheaf cohomology...
s.
Ringed spaces and locally ringed spaces
A pair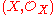 consisting of a topological space X and a sheaf of rings on X is called a ringed space
consisting of a topological space X and a sheaf of rings on X is called a ringed spaceRinged space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
. Many types of spaces can be defined as certain types of ringed spaces. The sheaf
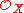 is called the structure sheaf of the space. A very common situation is when all the stalks of the structure sheaf are local ring
is called the structure sheaf of the space. A very common situation is when all the stalks of the structure sheaf are local ringLocal ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
s, in which case the pair is called a locally ringed space. Here are examples of definitions made in this way:
- An n-dimensional Ck manifold M is a locally ringed space whose structure sheaf is an
 -algebra and is locally isomorphic to the sheaf of Ck real-valued functions on Rn.
-algebra and is locally isomorphic to the sheaf of Ck real-valued functions on Rn. - A complex analytic spaceComplex analytic spaceIn mathematics, a complex analytic space is a generalization of a complex manifold which allows the presence of singularities. Complex analytic spaces are locally ringed spaces which are locally isomorphic to local model spaces, where a local model space is an open subset of the vanishing locus of...
is a locally ringed space whose structure sheaf is a -algebra and is locally isomorphic to the vanishing locus of a finite set of holomorphic functions together with the restriction (to the vanishing locus) of the sheaf of holomorphic functions on Cn for some n.
-algebra and is locally isomorphic to the vanishing locus of a finite set of holomorphic functions together with the restriction (to the vanishing locus) of the sheaf of holomorphic functions on Cn for some n. - A schemeScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
is a locally ringed space that is locally isomorphic to the spectrum of a ringSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
. - A semialgebraic spaceSemialgebraic spaceIn mathematics, especially in real algebraic geometry, a semialgebraic space is a space which is locally isomorphic to a semialgebraic set.-Definition:Let U be an open subset of Rn for some n...
is a locally ringed space that is locally isomorphic to a semialgebraic setSemialgebraic setIn mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
in Euclidean space together with its sheaf of semialgebraic functions.
Sheaves of modules
Let be a ringed space. A sheaf of modules is a sheaf
be a ringed space. A sheaf of modules is a sheaf 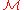 such that on every open set U of X,
such that on every open set U of X,  is an
is an 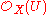 -module and for every inclusion of open sets V ⊆ U, the restriction map
-module and for every inclusion of open sets V ⊆ U, the restriction map  is a homomorphism of
is a homomorphism of 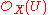 -modules.
-modules.Most important geometric objects are sheaves of modules. For example, there is a one-to-one correspondence between vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s and locally free sheaves of
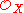 -modules. Sheaves of solutions to differential equations are D-module
-modules. Sheaves of solutions to differential equations are D-moduleD-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
s, that is, modules over the sheaf of differential operators.
A particularly important case are abelian sheaves, which are modules over the constant sheaf
 . Every sheaf of modules is an abelian sheaf.
. Every sheaf of modules is an abelian sheaf.Finiteness conditions for sheaves of modules
The condition that a module is finitely generated or finitely presented can also be formulated for a sheaf of modules.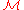 is finitely generated if, for every point x of X, there exists an open neighborhood U of x, a natural number n (possibly depending on U), and a surjective morphism of sheaves
is finitely generated if, for every point x of X, there exists an open neighborhood U of x, a natural number n (possibly depending on U), and a surjective morphism of sheaves 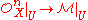 . Similarly,
. Similarly, 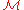 is finitely presented if in addition there exists a natural number m (again possibly depending on U) and a morphism of sheaves
is finitely presented if in addition there exists a natural number m (again possibly depending on U) and a morphism of sheaves  such that the sequence of morphisms
such that the sequence of morphisms  is exact. Equivalently, the kernel of the morphism
is exact. Equivalently, the kernel of the morphism 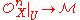 is itself a finitely generated sheaf.
is itself a finitely generated sheaf.These, however, are not the only possible finiteness conditions on a sheaf. The most important finiteness condition for a sheaf is coherence.
 is coherent if it is of finite type and if, for every open set U and every morphism of sheaves
is coherent if it is of finite type and if, for every open set U and every morphism of sheaves 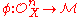 (not necessarily surjective), the kernel of φ is of finite type.
(not necessarily surjective), the kernel of φ is of finite type. 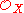 is coherent if it is coherent as a module over itself. Note that coherence is a strictly stronger condition than finite presentation:
is coherent if it is coherent as a module over itself. Note that coherence is a strictly stronger condition than finite presentation: 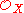 is always finitely presented as a module over itself, but it is not always coherent. For example, let X be a point, let
is always finitely presented as a module over itself, but it is not always coherent. For example, let X be a point, let  be the ring R = C[x1, x2, ...] of complex polynomials in countably many indeterminates. Choose n = 1, and for the morphism φ, take the map that sends every variable to zero. The kernel of this map is not finitely generated, so
be the ring R = C[x1, x2, ...] of complex polynomials in countably many indeterminates. Choose n = 1, and for the morphism φ, take the map that sends every variable to zero. The kernel of this map is not finitely generated, so 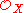 is not coherent.
is not coherent.The étalé space of a sheaf
In the examples above it was noted that some sheaves occur naturally as sheaves of sections. In fact, all sheaves of sets can be represented as sheaves of sections of a topological space called the étalé space, from the French word étalé etale, meaning roughly "spread out". If F is a sheaf over X, then the étalé space of F is a topological space E together with a local homeomorphismLocal homeomorphism
In mathematics, more specifically topology, a local homeomorphism is intuitively a function, f, between topological spaces that preserves local structure. Equivalently, one can cover the domain of this function by open sets, such that f restricted to each such open set is a homeomorphism onto its...
π: E → X such that the sheaf of sections of π is F. E is usually a very strange space, and even if the sheaf F arises from a natural topological situation, E may not have any clear topological interpretation. For example, if F is the sheaf of sections of a continuous function f : Y → X, then E = Y if and only if f is a local homeomorphism
Local homeomorphism
In mathematics, more specifically topology, a local homeomorphism is intuitively a function, f, between topological spaces that preserves local structure. Equivalently, one can cover the domain of this function by open sets, such that f restricted to each such open set is a homeomorphism onto its...
.
The étalé space E is constructed from the stalks of F over X. As a set, it is their disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
and π is the obvious map that takes the value x on the stalk of F over x ∈ X. The topology of E is defined as follows. For each element s of F(U) and each x in U, we get a germ of s at x. These germs determine points of E. For any U and s ∈ F(U), the union of these points (for all x ∈ U) is declared to be open in E. Notice that each stalk has the discrete topology as subspace topology. Two morphisms between sheaves determine a continuous map of the corresponding étalé spaces that is compatible with the projection maps (in the sense that every germ is mapped to a germ over the same point). This makes the construction into a functor.
The construction above determines an equivalence of categories
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
between the category of sheaves of sets on X and the category of étalé spaces over X. The construction of an étalé space can also be applied to a presheaf, in which case the sheaf of sections of the étalé space recovers the sheaf associated to the given presheaf.
This construction makes all sheaves into representable functor
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
s on certain categories of topological spaces. As above, let F be a sheaf on X, let E be its étalé space, and let π: E → X be the natural projection. Consider the category Top/X of topological spaces over X, that is, the category of topological spaces together with fixed continuous maps to X. Every object of this space is a continuous map f : Y → X, and a morphism from Y → X to Z → X is a continuous map Y → Z that commutes with the two maps to X. There is a functor Γ from Top/X to the category of sets which takes an object f : Y → X to (f−1F)(Y). For example, if i : U → X is the inclusion of an open subset, then Γ(i) = (i−1F)(U) agrees with the usual F(U), and if i : {x} → X is the inclusion of a point, then Γ({x}) = (i−1F)({x}) is the stalk of F at x. There is a natural isomorphism
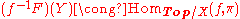
which shows that E represents the functor Γ.
E is constructed so that the projection map π is a covering map. In algebraic geometry, the natural analog of a covering map is called an étale morphism
Étale morphism
In algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
. Despite its similarity to "étalé", the word étale etal has a different meaning both in French and in mathematics. In particular, it is possible to turn E into a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
and π into a morphism of schemes in such a way that π retains the same universal property, but π is not in general an étale morphism because it is not quasi-finite. It is, however, formally étale.
The definition of sheaves by étalé spaces is older than the definition given earlier in the article. It is still common in some areas of mathematics such as mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
Sheaf cohomology
It was noted above that the functor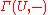 preserves isomorphisms and monomorphisms, but not epimorphisms. If F is a sheaf of abelian groups, or more generally a sheaf with values in an abelian category
preserves isomorphisms and monomorphisms, but not epimorphisms. If F is a sheaf of abelian groups, or more generally a sheaf with values in an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, then
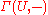 is actually a left exact functor. This means that it is possible to construct derived functor
is actually a left exact functor. This means that it is possible to construct derived functorDerived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s of
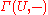 . These derived functors are called the cohomology groups (or modules) of F and are written
. These derived functors are called the cohomology groups (or modules) of F and are written 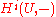 . Grothendieck proved in his Tohoku paper that every category of sheaves of abelian groups contains enough injective object
. Grothendieck proved in his Tohoku paper that every category of sheaves of abelian groups contains enough injective objectInjective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
s, so these derived functors always exist.
However, computing sheaf cohomology using injective resolutions is nearly impossible. In practice, it is much more common to find a different and more tractable resolution of F. A general construction is provided by Godement resolution
Godement resolution
The Godement resolution of a sheaf is a construction in homological algebra which allows one to view global, cohomological information about the sheaf in terms of local information coming from its stalks. It is useful for computing sheaf cohomology...
s, and particular resolutions may be constructed using soft sheaves, fine sheaves, and flabby sheaves (also known as flasque sheaves from the French flasque meaning flabby). As a consequence, it can become possible to compare sheaf cohomology with other cohomology theories. For example, the de Rham complex is a resolution of the constant sheaf
 on any smooth manifold, so the sheaf cohomology of
on any smooth manifold, so the sheaf cohomology of  is equal to its de Rham cohomology
is equal to its de Rham cohomologyDe Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
. In fact, comparing sheaf cohomology to de Rham cohomology and singular cohomology provides a proof of de Rham's theorem that the two cohomology theories are isomorphic.
A different approach is by Čech cohomology
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
. Čech cohomology was the first cohomology theory developed for sheaves and it is well-suited to concrete calculations. It relates sections on open subsets of the space to cohomology classes on the space. In most cases, Čech cohomology computes the same cohomology groups as the derived functor cohomology. However, for some pathological spaces, Čech cohomology will give the correct
 but incorrect higher cohomology groups. To get around this, Jean-Louis Verdier
but incorrect higher cohomology groups. To get around this, Jean-Louis VerdierJean-Louis Verdier
Jean-Louis Verdier was a French mathematician who worked, under the guidance of Alexander Grothendieck, on derived categories and Verdier duality...
developed hypercoverings. Hypercoverings not only give the correct higher cohomology groups but also allow the open subsets mentioned above to be replaced by certain morphisms from another space. This flexibility is necessary in some applications, such as the construction of Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
's mixed Hodge structures.
A much cleaner approach to the computation of some cohomology groups is the Borel–Bott–Weil theorem
Borel–Bott–Weil theorem
In mathematics, the Borel–Weil-Bott theorem is a basic result in the representation theory of Lie groups, showing how a family of representations can be obtained from holomorphic sections of certain complex vector bundles, and, more generally, from higher sheaf cohomology groups associated to such...
, which identifies the cohomology groups of some line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s on flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s with irreducible representations of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. This theorem can be used, for example, to easily compute the cohomology groups of all line bundles on projective space.
In many cases there is a duality theory for sheaves that generalizes Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
. See Grothendieck duality and Verdier duality
Verdier duality
In mathematics, Verdier duality is a generalization of the Poincaré duality of manifolds to locally compact spaces with singularities. Verdier duality was introduced by , as an analog for locally compact spaces of the coherent duality for schemes due to Grothendieck...
.
Sites and topoi
André WeilAndré Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
's Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
stated that there was a cohomology theory
Weil cohomology theory
In algebraic geometry, a Weil cohomology or Weil cohomology theory is a cohomology satisfying certain axioms concerning the interplay of algebraic cycles and cohomology groups. The name is in honor of André Weil...
for algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s that would give an analogue of the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. The only natural topology on such a variety, however, is the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, but sheaf cohomology in the Zariski topology is badly behaved because there are very few open sets. Alexandre Grothendieck solved this problem by introducing Grothendieck topologies
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...
, which axiomatize the notion of covering. Grothendieck's insight was that the definition of a sheaf depends only on the open sets of a topological space, not on the individual points. Once he had axiomatized the notion of covering, open sets could be replaced by other objects. A presheaf takes each one of these objects to data, just as before, and a sheaf is a presheaf that satisfies the gluing axiom with respect to our new notion of covering. This allowed Grothendieck to define étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
and l-adic cohomology, which eventually were used to prove the Weil conjectures.
A category with a Grothendieck topology is called a site. A category of sheaves on a site is called a topos or a Grothendieck topos. The notion of a topos was later abstracted by William Lawvere
William Lawvere
Francis William Lawvere is a mathematician known for his work in category theory, topos theory and the philosophy of mathematics.-Biography:...
and Miles Tierney to define an elementary topos, which has connections to mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
.
History
The first origins of sheaf theory are hard to pin down — they may be co-extensive with the idea of analytic continuationAnalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
. It took about 15 years for a recognisable, free-standing theory of sheaves to emerge from the foundational work on cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
.
- 1936 Eduard ČechEduard CechEduard Čech was a Czech mathematician born in Stračov, Bohemia . His research interests included projective differential geometry and topology. In 1921–1922 he collaborated with Guido Fubini in Turin...
introduces the nerveNerve of an open coveringIn mathematics, the nerve of an open covering is a construction in topology, of an abstract simplicial complex from an open covering of a topological space X.The notion of nerve was introduced by Pavel Alexandrov....
construction, for associating a simplicial complexSimplicial complexIn mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
to an open covering. - 1938 Hassler WhitneyHassler WhitneyHassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
gives a 'modern' definition of cohomology, summarizing the work since J. W. AlexanderJames Waddell Alexander IIJames Waddell Alexander II was a mathematician and topologist of the pre-World War II era and part of an influential Princeton topology elite, which included Oswald Veblen, Solomon Lefschetz, and others...
and Kolmogorov first defined cochains. - 1943 Norman SteenrodNorman SteenrodNorman Earl Steenrod was a preeminent mathematician most widely known for his contributions to the field of algebraic topology.-Life:...
publishes on homology with local coefficientsLocal coefficientsIn mathematics, local coefficients is an idea from algebraic topology, a kind of half-way stage between homology theory or cohomology theory with coefficients in the usual sense, in a fixed abelian group A, and general sheaf cohomology which, roughly speaking, allows coefficients to vary from point...
. - 1945 Jean LerayJean LerayJean Leray was a French mathematician, who worked on both partial differential equations and algebraic topology....
publishes work carried out as a prisoner of warPrisoner of warA prisoner of war or enemy prisoner of war is a person, whether civilian or combatant, who is held in custody by an enemy power during or immediately after an armed conflict...
, motivated by proving fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
theorems for application to PDEPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
theory; it is the start of sheaf theory and spectral sequenceSpectral sequenceIn homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
s. - 1947 Henri CartanHenri CartanHenri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
reproves the de Rham theorem by sheaf methods, in correspondence with André WeilAndré WeilAndré Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
(see De Rham-Weil theoremDe Rham-Weil theoremIn algebraic topology, the De Rham-Weil theorem allows computation of sheaf cohomology using an acyclic resolution of the sheaf in question.Let \mathcal F be a sheaf on a topological space X and \mathcal F^\bullet a resolution of \mathcal F by acyclic sheaves...
). Leray gives a sheaf definition in his courses via closed sets (the later carapaces). - 1948 The Cartan seminar writes up sheaf theory for the first time.
- 1950 The "second edition" sheaf theory from the Cartan seminar: the sheaf space (espace étalé) definition is used, with stalkwise structure. SupportSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
s are introduced, and cohomology with supports. Continuous mappings give rise to spectral sequences. At the same time Kiyoshi OkaKiyoshi Okawas a Japanese mathematician who did fundamental work in the theory of several complex variables. He was born in Osaka. He went to Kyoto Imperial University in 1919, turning to mathematics in 1923 and graduating in 1924....
introduces an idea (adjacent to that) of a sheaf of ideals, in several complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. - 1951 The Cartan seminar proves the Theorems A and B based on Oka's work.
- 1953 The finiteness theorem for coherent sheavesCoherent sheafIn mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
in the analytic theory is proved by Cartan and Jean-Pierre SerreJean-Pierre SerreJean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
, as is Serre dualitySerre dualityIn algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
. - 1954 Serre's paper Faisceaux algébriques cohérents (published in 1955) introduces sheaves into algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. These ideas are immediately exploited by Hirzebruch, who writes a major 1956 book on topological methods. - 1955 Alexander GrothendieckAlexander GrothendieckAlexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
in lectures in KansasKansasKansas is a US state located in the Midwestern United States. It is named after the Kansas River which flows through it, which in turn was named after the Kansa Native American tribe, which inhabited the area. The tribe's name is often said to mean "people of the wind" or "people of the south...
defines abelian categoryAbelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
and presheaf, and by using injective resolutions allows direct use of sheaf cohomology on all topological spaces, as derived functorDerived functorIn mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s. - 1956 Oscar ZariskiOscar ZariskiOscar Zariski was a Russian mathematician and one of the most influential algebraic geometers of the 20th century.-Education:...
's report Algebraic sheaf theory - 1957 Grothendieck's Tohoku paper rewrites homological algebraHomological algebraHomological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
; he proves Grothendieck duality (i.e., Serre duality for possibly singularMathematical singularityIn mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
algebraic varieties). - 1957 onwards: Grothendieck extends sheaf theory in line with the needs of algebraic geometry, introducing: schemeScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s and general sheaves on them, local cohomologyLocal cohomologyIn mathematics, local cohomology is a chapter of homological algebra and sheaf theory introduced into algebraic geometry by Alexander Grothendieck. He developed it in seminars in 1961 at Harvard University, and 1961-2 at IHES. It was later written up as SGA2...
, derived categoriesDerived categoryIn mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
(with Verdier), and Grothendieck topologies. There emerges also his influential schematic idea of 'six operations' in homological algebra. - 1958 Godement's book on sheaf theory is published. At around this time Mikio SatoMikio Satois a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
proposes his hyperfunctionHyperfunctionIn mathematics, hyperfunctions are generalizations of functions, as a 'jump' from one holomorphic function to another at a boundary, and can be thought of informally as distributions of infinite order...
s, which will turn out to have sheaf-theoretic nature.
At this point sheaves had become a mainstream part of mathematics, with use by no means restricted to algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. It was later discovered that the logic in categories of sheaves is intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
(this observation is now often referred to as Kripke–Joyal semantics, but probably should be attributed to a number of authors). This shows that some of the facets of sheaf theory can also be traced back as far as Leibniz.

