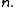Locally free sheaf
Encyclopedia
In sheaf theory, a field of mathematics, a sheaf of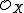 
-modules 
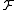on a ringed space
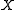is called locally free if for each point 
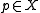, there is an open
neighborhood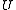
of 
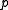such that 
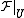is free
as an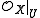
-module. This implies that 
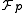, the stalk of 
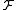at 
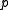, is free as a 
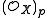-module for all 
. The converse is true if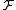 
is moreover coherent
. If
is of finite rank 
for every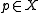 
, then 
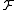is said to be of rank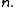 
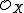-modules 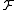on a ringed spaceRinged space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
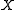is called locally free if for each point 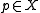, there is an openTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
neighborhood
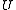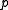of such that 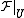is freeFree module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
as an
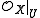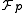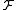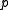-module. This implies that , the stalk of at , is free as a 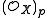-module for all . The converse is true if 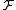is moreover coherentCoherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
. If
is of finite rank for every 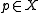, then 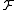is said to be of rank