Semialgebraic set
Encyclopedia
In mathematics
, a semialgebraic set is a subset S of Rn for some real closed field
R (for example R could be the field of real numbers) defined by a finite sequence of polynomial equations (of the form
) and inequalities (of the form 
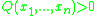), or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph. Such sets and functions are mainly studied in real algebraic geometry
which is the appropriate framework for algebraic geometry
over the real numbers.
says that they are also closed under the projection operation: in other words a semialgebraic set projected onto a linear subspace
yields another such (as case of elimination of quantifiers). These properties together mean that semialgebraic sets form an o-minimal structure on R.
A semialgebraic set (or function) is said to be defined over a subring A of R if there is some description as in the definition, where the polynomials can be chosen to have coefficients in A.
On a dense open subset of the semialgebraic set S, it is (locally) a submanifold
. One can define the dimension of S to be the largest dimension at points at which it is a submanifold. It is not hard to see that a semialgebraic set lies inside an algebraic subvariety of the same dimension.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a semialgebraic set is a subset S of Rn for some real closed field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
R (for example R could be the field of real numbers) defined by a finite sequence of polynomial equations (of the form
) and inequalities (of the form 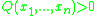), or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph. Such sets and functions are mainly studied in real algebraic geometryReal algebraic geometry
In mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....
which is the appropriate framework for algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
over the real numbers.
Properties
Similarly to algebraic subvarieties, finite unions and intersections of semialgebraic sets are still semialgebraic sets. Furthermore, unlike subvarieties, the complement of a semialgebraic set is again semialgebraic. Finally, and most importantly, the Tarski–Seidenberg theoremTarski–Seidenberg theorem
In mathematics, the Tarski–Seidenberg theorem states that a set in -dimensional space defined by polynomial identities and inequalities can be projected down onto n-dimensional space, and the resulting set is still definable in terms of polynomial identities and inequalities...
says that they are also closed under the projection operation: in other words a semialgebraic set projected onto a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
yields another such (as case of elimination of quantifiers). These properties together mean that semialgebraic sets form an o-minimal structure on R.
A semialgebraic set (or function) is said to be defined over a subring A of R if there is some description as in the definition, where the polynomials can be chosen to have coefficients in A.
On a dense open subset of the semialgebraic set S, it is (locally) a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
. One can define the dimension of S to be the largest dimension at points at which it is a submanifold. It is not hard to see that a semialgebraic set lies inside an algebraic subvariety of the same dimension.