
Algebraic geometry
Encyclopedia
Algebraic geometry is a branch of mathematics
which combines techniques of abstract algebra
, especially commutative algebra
, with the language and the problems of geometry
. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex analysis
, topology
and number theory
. Initially a study of systems of polynomial equations
in several variables, the subject of algebraic geometry starts where equation solving
leaves off, and it becomes even more important to understand the intrinsic properties of the totality of solutions of a system of equations, than to find some solution; this leads into some of the deepest waters in the whole of mathematics, both conceptually and in terms of technique.
The fundamental objects of study in algebraic geometry are algebraic varieties
, geometric manifestations of solutions of systems of polynomial equations
. Plane algebraic curves, which include lines
, circle
s, parabola
s, lemniscate
s, and Cassini oval
s, form one of the best studied classes of algebraic varieties. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve relative position of different curves and relations between the curves given by different equations.
Descartes's idea of coordinates is central to algebraic geometry, but it has undergone a series of remarkable transformations beginning in the early 19th century. Before then, the coordinates were assumed to be tuple
s of real number
s, but this changed when first complex number
s, and then elements of an arbitrary field
became acceptable. Homogeneous coordinates
of projective geometry
offered an extension of the notion of coordinate system in a different direction, and enriched the scope of algebraic geometry. Much of the development of algebraic geometry in the 20th century occurred within an abstract algebraic framework, with increasing emphasis being placed on 'intrinsic' properties of algebraic varieties not dependent on any particular way of embedding the variety in an ambient coordinate space; this parallels developments in topology
and complex geometry
.
One key distinction between classical projective geometry of 19th century and modern algebraic geometry, in the form given to it by Grothendieck and Serre
, is that the former is concerned with the more geometric notion of a point, while the latter emphasizes the more analytic concepts of a regular function
and a regular map
and extensively draws on sheaf theory. Another important difference lies in the scope of the subject. Grothendieck's idea of scheme
provides the language and the tools for geometric treatment of arbitrary commutative ring
s and, in particular, bridges algebraic geometry with algebraic number theory
. Andrew Wiles
's celebrated proof of Fermat's last theorem
is a vivid testament to the power of this approach. André Weil
, Grothendieck, and Deligne
also demonstrated
that the fundamental ideas of topology of manifolds have deep analogues in algebraic geometry over finite field
s.
 In classical algebraic geometry, the main objects of interest are the vanishing sets of collections of polynomial
In classical algebraic geometry, the main objects of interest are the vanishing sets of collections of polynomial
s, meaning the set of all points that simultaneously satisfy one or more polynomial equations
. For instance, the two-dimensional sphere
in three-dimensional Euclidean space
R3 could be defined as the set of all points (x,y,z) with
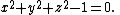
A "slanted" circle in R3 can be defined as the set of all points (x,y,z) which satisfy the two polynomial equations
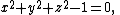
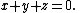
k. In classical algebraic geometry, this field was always the complex numbers C, but many of the same results are true if we assume only that k is algebraically closed
. We consider the affine space
of dimension n over k, denoted An(k) (or more simply An, when k is clear from the context). When one fixes a coordinates system, one may identify An(k) with kn. The purpose of not working with kn is to emphasize that one "forgets" the vector space structure that kn carries.
A function f : An → A1 is said to be regular if it can be written as a polynomial, that is, if there is a polynomial p in k[x1,...,xn] such that f(t1,...,tn) = p(t1,...,tn) for every point (t1,...,tn) of An.
Regular functions on affine n-space are thus exactly the same as polynomials over k in n variables. We will refer to the set of all regular functions on An as k[An].
We say that a polynomial vanishes at a point if evaluating it at that point gives zero. Let S be a set of polynomials in k[An]. The vanishing set of S (or vanishing locus) is the set V(S) of all points in An where every polynomial in S vanishes. In other words,
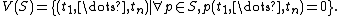
A subset of An which is V(S), for some S, is called an algebraic set. The V stands for variety (a specific type of algebraic set to be defined below).
Given a subset U of An, can one recover the set of polynomials which generate it? If U is any subset of An, define I(U) to be the set of all polynomials whose vanishing set contains U. The I stands for ideal
: if two polynomials f and g both vanish on U, then f+g vanishes on U, and if h is any polynomial, then hf vanishes on U, so I(U) is always an ideal of k[An].
Two natural questions to ask are:
The answer to the first question is provided by introducing the Zariski topology
, a topology on An which directly reflects the algebraic structure of k[An]. Then U = V(I(U)) if and only if U is a Zariski-closed set. The answer to the second question is given by Hilbert's Nullstellensatz
. In one of its forms, it says that I(V(S)) is the prime radical of the ideal generated by S. In more abstract language, there is a Galois connection
, giving rise to two closure operator
s; they can be identified, and naturally play a basic role in the theory; the example is elaborated at Galois connection.
For various reasons we may not always want to work with the entire ideal corresponding to an algebraic set U. Hilbert's basis theorem
implies that ideals in k[An] are always finitely generated.
An algebraic set is called irreducible
if it cannot be written as the union of two smaller algebraic sets. An irreducible algebraic set is also called a variety
. It turns out that an algebraic set is a variety if and only if the polynomials defining it generate a prime ideal
of the polynomial ring.
s are the natural maps on topological space
s and smooth function
s are the natural maps on differentiable manifold
s, there is a natural class of functions on an algebraic set, called regular functions. A regular function on an algebraic set V contained in An is defined to be the restriction of a regular function on An, in the sense we defined above.
It may seem unnaturally restrictive to require that a regular function always extend to the ambient space, but it is very similar to the situation in a normal
topological space
, where the Tietze extension theorem guarantees that a continuous function on a closed subset always extends to the ambient topological space.
Just as with the regular functions on affine space
, the regular functions on V form a ring, which we denote by k[V]. This ring is called the coordinate ring of V.
Since regular functions on V come from regular functions on An, there should be a relationship between their coordinate rings. Specifically, to get a function in k[V] we took a function in k[An], and we said that it was the same as another function if they gave the same values when evaluated on V. This is the same as saying that their difference is zero on V. From this we can see that k[V] is the quotient k[An]/I(V).
of f.
If V' is a variety contained in Am, we say that f is a regular function from V to V' if the range of f is contained in V' .
This makes the collection of all affine varieties into a category
, where the objects are affine varieties and the morphism
s are regular maps. The following theorem characterizes the category of affine varieties:
. As x increases, the slope of the line from the origin to the point (x, x2) becomes larger and larger. As x decreases, the slope of the same line becomes smaller and smaller.
Compare this to the variety V(y − x3). This is a cubic equation. As x increases, the slope of the line from the origin to the point (x, x3) becomes larger and larger just as before. But unlike before, as x decreases, the slope of the same line again becomes larger and larger. So the behavior "at infinity" of V(y − x3) is different from the behavior "at infinity" of V(y − x2). It is, however, difficult to make the concept of "at infinity" meaningful, if we restrict to working in affine space.
The remedy to this is to work in projective space
. Projective space has properties analogous to those of a compact
Hausdorff space
. Among other things, it lets us make precise the notion of "at infinity" by including extra points. The behavior of a variety at those extra points then gives us more information about it. As it turns out, V(y − x3) has a singularity
at one of those extra points, but V(y − x2) is smooth.
While projective geometry
was originally established on a synthetic
foundation, the use of homogeneous coordinates
allowed the introduction of algebraic techniques. Furthermore, the introduction of projective techniques made many theorems in algebraic geometry simpler and sharper: For example, Bézout's theorem
on the number of intersection points between two varieties can be stated in its sharpest form only in projective space. For this reason, projective space plays a fundamental role in algebraic geometry.
s, ind-schemes, algebraic space
s, algebraic stacks and so on. The need for this arises already from the useful ideas within theory of varieties, e.g. the formal functions of Zariski can be accommodated by introducing nilpotent elements in structure rings; considering spaces of loops and arcs, constructing quotients by group actions and developing formal grounds for natural intersection theory and deformation theory lead to some of the further extensions.
Most remarkably, in late 1950s, algebraic varieties were subsumed into Alexander Grothendieck
's concept of a scheme
. Their local objects are affine schemes or prime spectra which are locally ringed spaces which form a category which is antiequivalent to the category of commutative unital rings, extending the duality between the category of affine algebraic varieties over a field k, and the category of finitely generated reduced k-algebras. The gluing is along Zariski topology; one can glue within the category of locally ringed spaces, but also, using the Yoneda embedding, within the more abstract category of presheaves of sets over the category of affine schemes. The Zariski topology in the set theoretic sense is then replaced by a Zariski topology in the sense of Grothendieck topology
. Grothendieck introduced Grothendieck topologies having in mind more exotic but geometrically finer and more sensitive examples than the crude Zariski topology, namely the étale topology
, and the two flat Grothendieck topologies: ffpf and fpqc; nowadays some other examples became prominent including Nisnevich topology
. Sheaves can be furthermore generalized to stacks in the sense of Grothendieck, usually with some additional representability conditions leading to Artin stacks and, even finer, Deligne-Mumford stacks, both often called algebraic stacks.
Sometimes other algebraic sites replace the category of affine schemes. For example, Nikolai Durov
has introduced commutative algebraic monads as a generalization of local objects in a generalized algebraic geometry. Versions of a tropical geometry, of an absolute geometry over a field of one element and an algebraic analogue of Arakelov's geometry were realized in this setup.
Another formal generalization is possible to Universal algebraic geometry
in which every variety of algebra
has its own algebraic geometry. The term variety of algebra should not be confused with algebraic variety.
The language of schemes, stacks and generalizations has proved to be a valuable way of dealing with geometric concepts and became cornerstones of modern algebraic geometry.
Algebraic stacks can be further generalized and for many practical questions like deformation theory and intersection theory, this is often the most natural approach. One can extend the Grothendieck site of affine schemes to a higher categorical
site of derived affine schemes, by replacing the commutative rings with an infinity category of differential graded commutative algebras, or of simplicial commutative rings or a similar category with an appropriate variant of a Grothendieck topology. One can also replace presheaves of sets by presheaves of simplicial sets (or of infinity groupoids). Then, in presence of an appropriate homotopic machinery one can develop a notion of derived stack as such a presheaf on the infinity category of derived affine schemes, which is satifsying certain infinite categorical version of a sheaf axiom (and to be algebraic, inductively a sequence of representability conditions). Quillen model categories, Segal categories and quasicategories are some of the most often used tools to formalize this yielding the derived algebraic geometry, introduced by the school of Carlos Simpson, including Andre Hirschowitz, Bertrand Toën, Gabrielle Vezzosi, Michel Vaquié and others; and developed further by Jacob Lurie
, Bertrand Toën, and Gabrielle Vezzosi. Another (noncommutative) version of derived algebraic geometry, using A-infinity categories has been developed from early 1990-s by Maxim Kontsevich
and followers.
from the 5th century BC. The Delian problem, for instance, was to construct a length x so that the cube of side x contained the same volume as the rectangular box a2b for given sides a and b. Menechmus (circa 350 BC) considered the problem geometrically by intersecting the pair of plane conics ay = x2 and xy = ab. The later work, in the 3rd century BC, of Archimedes
and Apollonius
studied more systematically problems on conic sections, and also involved the use of coordinates. The Arab mathematicians were able to solve by purely algebraic means certain cubic equations, and then to interpret the results geometrically. This was done, for instance, by Ibn al-Haytham in the 10th century AD. Subsequently, Persian
mathematician Omar Khayyám
(born 1048 A.D.) discovered the general method of solving cubic equations by intersecting a parabola with a circle. Each of these early developments in algebraic geometry dealt with questions of finding and describing the intersections of algebraic curves.
Such techniques of applying geometrical constructions to algebraic problems were also adopted by a number of Renaissance
mathematicians such as Gerolamo Cardano
and Niccolò Fontana "Tartaglia"
on their studies of the cubic equation. The geometrical approach to construction problems, rather than the algebraic one, was favored by most 16th and 17th century mathematicians, notably Blaise Pascal
who argued against the use of algebraic and analytical methods in geometry. The French mathematicians Franciscus Vieta and later René Descartes
and Pierre de Fermat
revolutionized the conventional way of thinking about construction problems through the introduction of coordinate geometry. They were interested primarily in the properties of algebraic curves, such as those defined by Diophantine equations (in the case of Fermat), and the algebraic reformulation of the classical Greek works on conics and cubics (in the case of Descartes).
During the same period, Blaise Pascal and Gérard Desargues
approached geometry from a different perspective, developing the synthetic
notions of projective geometry
. Pascal and Desargues also studied curves, but from the purely geometrical point of view: the analog of the Greek ruler and compass construction. Ultimately, the analytic geometry
of Descartes and Fermat won out, for it supplied the 18th century mathematicians with concrete quantitative tools needed to study physical problems using the new calculus of Newton
and Leibniz. However, by the end of the 18th century, most of the algebraic character of coordinate geometry was subsumed by the calculus of infinitesimals of Lagrange
and Euler.
and Abelian integrals in order to bring the old algebraic ideas back into the geometrical fold. The first of these new developments was seized up by Edmond Laguerre
and Arthur Cayley
, who attempted to ascertain the generalized metric properties of projective space. Cayley introduced the idea of homogeneous polynomial forms, and more specifically quadratic form
s, on projective space. Subsequently, Felix Klein
studied projective geometry (along with other sorts of geometry) from the viewpoint that the geometry on a space is encoded in a certain class of transformations on the space. By the end of the 19th century, projective geometers were studying more general kinds of transformations on figures in projective space. Rather than the projective linear transformations which were normally regarded as giving the fundamental Kleinian geometry on projective space, they concerned themselves also with the higher degree birational transformations. This weaker notion of congruence would later lead members of the 20th century Italian school of algebraic geometry
to classify algebraic surface
s up to birational isomorphism.
The second early 19th century development, that of Abelian integrals, would lead Bernhard Riemann
to the development of Riemann surface
s.
, André Weil
and others attempted to develop a rigorous foundation for algebraic geometry based on contemporary commutative algebra
, including valuation theory and the theory of ideals
.
In the 1950s and 1960s Jean-Pierre Serre
and Alexander Grothendieck
recast the foundations making use of sheaf theory. Later, from about 1960, and largely spearheaded by Grothendieck, the idea of schemes
was worked out, in conjunction with a very refined apparatus of homological techniques
. After a decade of rapid development the field stabilized in the 1970s, and new applications were made, both to number theory
and to more classical geometric questions on algebraic varieties, singularities
and moduli
.
An important class of varieties, not easily understood directly from their defining equations, are the abelian varieties
, which are the projective varieties whose points form an abelian group
. The prototypical examples are the elliptic curve
s, which have a rich theory. They were instrumental in the proof of Fermat's last theorem
and are also used in elliptic curve cryptography
.
While much of algebraic geometry is concerned with abstract and general statements about varieties, methods for effective computation with concretely-given polynomials have also been developed. The most important is the technique of Gröbner bases
which is employed in all computer algebra systems. Based on these methods, several solvers may compute all the solutions of a system of polynomial equations
whose associated variety has dimension zero and thus consists in a finite number of points.
, control theory
, robotics
, error-correcting codes, phylogenetics
and geometric modelling. There are also connections to string theory
, game theory
, graph matchings, soliton
s and integer programming
. Google Scholar lists hundreds of more studies on algebraic geometry in biology, chemistry, economics, physics and of course other areas of mathematics.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
which combines techniques of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, especially commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, with the language and the problems of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. Initially a study of systems of polynomial equations
Systems of polynomial equations
A system of polynomial equations is a set of simultaneous equations f1 = 0, ..., fh = 0 where the fi are polynomials in several variables, say x1, ..., xn, over some field k....
in several variables, the subject of algebraic geometry starts where equation solving
Equation solving
In mathematics, to solve an equation is to find what values fulfill a condition stated in the form of an equation . These expressions contain one or more unknowns, which are free variables for which values are sought that cause the condition to be fulfilled...
leaves off, and it becomes even more important to understand the intrinsic properties of the totality of solutions of a system of equations, than to find some solution; this leads into some of the deepest waters in the whole of mathematics, both conceptually and in terms of technique.
The fundamental objects of study in algebraic geometry are algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, geometric manifestations of solutions of systems of polynomial equations
Systems of polynomial equations
A system of polynomial equations is a set of simultaneous equations f1 = 0, ..., fh = 0 where the fi are polynomials in several variables, say x1, ..., xn, over some field k....
. Plane algebraic curves, which include lines
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s, parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
s, lemniscate
Lemniscate
In algebraic geometry, a lemniscate refers to any of several figure-eight or ∞ shaped curves. It may refer to:*The lemniscate of Bernoulli, often simply called the lemniscate, the locus of points whose product of distances from two foci equals the square of half the interfocal distance*The...
s, and Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
s, form one of the best studied classes of algebraic varieties. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve relative position of different curves and relations between the curves given by different equations.
Descartes's idea of coordinates is central to algebraic geometry, but it has undergone a series of remarkable transformations beginning in the early 19th century. Before then, the coordinates were assumed to be tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, but this changed when first complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, and then elements of an arbitrary field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
became acceptable. Homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
of projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
offered an extension of the notion of coordinate system in a different direction, and enriched the scope of algebraic geometry. Much of the development of algebraic geometry in the 20th century occurred within an abstract algebraic framework, with increasing emphasis being placed on 'intrinsic' properties of algebraic varieties not dependent on any particular way of embedding the variety in an ambient coordinate space; this parallels developments in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and complex geometry
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
.
One key distinction between classical projective geometry of 19th century and modern algebraic geometry, in the form given to it by Grothendieck and Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
, is that the former is concerned with the more geometric notion of a point, while the latter emphasizes the more analytic concepts of a regular function
Regular function
In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
and a regular map
Regular map (algebraic geometry)
In algebraic geometry, a regular map between affine varieties is a mapping which is given by polynomials. For example, if X and Y are subvarieties of An resp...
and extensively draws on sheaf theory. Another important difference lies in the scope of the subject. Grothendieck's idea of scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
provides the language and the tools for geometric treatment of arbitrary commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s and, in particular, bridges algebraic geometry with algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
. Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
's celebrated proof of Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
is a vivid testament to the power of this approach. André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, Grothendieck, and Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
also demonstrated
Weil cohomology theory
In algebraic geometry, a Weil cohomology or Weil cohomology theory is a cohomology satisfying certain axioms concerning the interplay of algebraic cycles and cohomology groups. The name is in honor of André Weil...
that the fundamental ideas of topology of manifolds have deep analogues in algebraic geometry over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
Zeros of simultaneous polynomials

Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, meaning the set of all points that simultaneously satisfy one or more polynomial equations
Systems of polynomial equations
A system of polynomial equations is a set of simultaneous equations f1 = 0, ..., fh = 0 where the fi are polynomials in several variables, say x1, ..., xn, over some field k....
. For instance, the two-dimensional sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3 could be defined as the set of all points (x,y,z) with
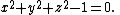
A "slanted" circle in R3 can be defined as the set of all points (x,y,z) which satisfy the two polynomial equations
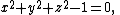
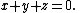
Affine varieties
First we start with a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k. In classical algebraic geometry, this field was always the complex numbers C, but many of the same results are true if we assume only that k is algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
. We consider the affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
of dimension n over k, denoted An(k) (or more simply An, when k is clear from the context). When one fixes a coordinates system, one may identify An(k) with kn. The purpose of not working with kn is to emphasize that one "forgets" the vector space structure that kn carries.
A function f : An → A1 is said to be regular if it can be written as a polynomial, that is, if there is a polynomial p in k[x1,...,xn] such that f(t1,...,tn) = p(t1,...,tn) for every point (t1,...,tn) of An.
Regular functions on affine n-space are thus exactly the same as polynomials over k in n variables. We will refer to the set of all regular functions on An as k[An].
We say that a polynomial vanishes at a point if evaluating it at that point gives zero. Let S be a set of polynomials in k[An]. The vanishing set of S (or vanishing locus) is the set V(S) of all points in An where every polynomial in S vanishes. In other words,
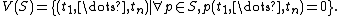
A subset of An which is V(S), for some S, is called an algebraic set. The V stands for variety (a specific type of algebraic set to be defined below).
Given a subset U of An, can one recover the set of polynomials which generate it? If U is any subset of An, define I(U) to be the set of all polynomials whose vanishing set contains U. The I stands for ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
: if two polynomials f and g both vanish on U, then f+g vanishes on U, and if h is any polynomial, then hf vanishes on U, so I(U) is always an ideal of k[An].
Two natural questions to ask are:
- Given a subset U of An, when is U = V(I(U))?
- Given a set S of polynomials, when is S = I(V(S))?
The answer to the first question is provided by introducing the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, a topology on An which directly reflects the algebraic structure of k[An]. Then U = V(I(U)) if and only if U is a Zariski-closed set. The answer to the second question is given by Hilbert's Nullstellensatz
Hilbert's Nullstellensatz
Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
. In one of its forms, it says that I(V(S)) is the prime radical of the ideal generated by S. In more abstract language, there is a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
, giving rise to two closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
s; they can be identified, and naturally play a basic role in the theory; the example is elaborated at Galois connection.
For various reasons we may not always want to work with the entire ideal corresponding to an algebraic set U. Hilbert's basis theorem
Hilbert's basis theorem
In mathematics, specifically commutative algebra, Hilbert's basis theorem states that every ideal in the ring of multivariate polynomials over a Noetherian ring is finitely generated. This can be translated into algebraic geometry as follows: every algebraic set over a field can be described as the...
implies that ideals in k[An] are always finitely generated.
An algebraic set is called irreducible
Irreducible component
In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
if it cannot be written as the union of two smaller algebraic sets. An irreducible algebraic set is also called a variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. It turns out that an algebraic set is a variety if and only if the polynomials defining it generate a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
of the polynomial ring.
Regular functions
Just as continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s are the natural maps on topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s are the natural maps on differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s, there is a natural class of functions on an algebraic set, called regular functions. A regular function on an algebraic set V contained in An is defined to be the restriction of a regular function on An, in the sense we defined above.
It may seem unnaturally restrictive to require that a regular function always extend to the ambient space, but it is very similar to the situation in a normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, where the Tietze extension theorem guarantees that a continuous function on a closed subset always extends to the ambient topological space.
Just as with the regular functions on affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, the regular functions on V form a ring, which we denote by k[V]. This ring is called the coordinate ring of V.
Since regular functions on V come from regular functions on An, there should be a relationship between their coordinate rings. Specifically, to get a function in k[V] we took a function in k[An], and we said that it was the same as another function if they gave the same values when evaluated on V. This is the same as saying that their difference is zero on V. From this we can see that k[V] is the quotient k[An]/I(V).
The category of affine varieties
Using regular functions from an affine variety to A1, we can define regular functions from one affine variety to another. First we will define a regular function from a variety into affine space: Let V be a variety contained in An. Choose m regular functions on V, and call them f1, ..., fm. We define a regular function f from V to Am by letting f(t1, ..., tn) = (f1, ..., fm). In other words, each fi determines one coordinate of the rangeRange (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of f.
If V
This makes the collection of all affine varieties into a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, where the objects are affine varieties and the morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s are regular maps. The following theorem characterizes the category of affine varieties:
- The category of affine varieties is the opposite categoryDual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
to the category of finitely generated integral k-algebrasAlgebra over a fieldIn mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
and their homomorphisms.
Projective space
Consider the variety V(y − x2). If we draw it, we get a parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. As x increases, the slope of the line from the origin to the point (x, x2) becomes larger and larger. As x decreases, the slope of the same line becomes smaller and smaller.
Compare this to the variety V(y − x3). This is a cubic equation. As x increases, the slope of the line from the origin to the point (x, x3) becomes larger and larger just as before. But unlike before, as x decreases, the slope of the same line again becomes larger and larger. So the behavior "at infinity" of V(y − x3) is different from the behavior "at infinity" of V(y − x2). It is, however, difficult to make the concept of "at infinity" meaningful, if we restrict to working in affine space.
The remedy to this is to work in projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. Projective space has properties analogous to those of a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. Among other things, it lets us make precise the notion of "at infinity" by including extra points. The behavior of a variety at those extra points then gives us more information about it. As it turns out, V(y − x3) has a singularity
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
at one of those extra points, but V(y − x2) is smooth.
While projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
was originally established on a synthetic
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
foundation, the use of homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
allowed the introduction of algebraic techniques. Furthermore, the introduction of projective techniques made many theorems in algebraic geometry simpler and sharper: For example, Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
on the number of intersection points between two varieties can be stated in its sharpest form only in projective space. For this reason, projective space plays a fundamental role in algebraic geometry.
The modern viewpoint
The modern approaches to algebraic geometry redefine and effectively extend the range of basic objects in various levels of generality to schemes, formal schemeFormal scheme
In mathematics, specifically in algebraic geometry, a formal scheme is a type of space which includes data about its surroundings. Unlike an ordinary scheme, a formal scheme includes infinitesimal data that, in effect, points in a direction off of the scheme...
s, ind-schemes, algebraic space
Algebraic space
In mathematics, an algebraic space is a generalization of the schemes of algebraic geometry introduced by Michael Artin for use in deformation theory...
s, algebraic stacks and so on. The need for this arises already from the useful ideas within theory of varieties, e.g. the formal functions of Zariski can be accommodated by introducing nilpotent elements in structure rings; considering spaces of loops and arcs, constructing quotients by group actions and developing formal grounds for natural intersection theory and deformation theory lead to some of the further extensions.
Most remarkably, in late 1950s, algebraic varieties were subsumed into Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
's concept of a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. Their local objects are affine schemes or prime spectra which are locally ringed spaces which form a category which is antiequivalent to the category of commutative unital rings, extending the duality between the category of affine algebraic varieties over a field k, and the category of finitely generated reduced k-algebras. The gluing is along Zariski topology; one can glue within the category of locally ringed spaces, but also, using the Yoneda embedding, within the more abstract category of presheaves of sets over the category of affine schemes. The Zariski topology in the set theoretic sense is then replaced by a Zariski topology in the sense of Grothendieck topology
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...
. Grothendieck introduced Grothendieck topologies having in mind more exotic but geometrically finer and more sensitive examples than the crude Zariski topology, namely the étale topology
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
, and the two flat Grothendieck topologies: ffpf and fpqc; nowadays some other examples became prominent including Nisnevich topology
Nisnevich topology
In algebraic geometry, the Nisnevich topology, sometimes called the completely decomposed topology, is a Grothendieck topology on the category of schemes which has been used in algebraic K-theory, A¹ homotopy theory, and the theory of motives...
. Sheaves can be furthermore generalized to stacks in the sense of Grothendieck, usually with some additional representability conditions leading to Artin stacks and, even finer, Deligne-Mumford stacks, both often called algebraic stacks.
Sometimes other algebraic sites replace the category of affine schemes. For example, Nikolai Durov
Nikolai Durov
Nikolai Durov is a Russian mathematician and programmer. He is one of the founders of Vkontakte.ru web site.- Early life and education :...
has introduced commutative algebraic monads as a generalization of local objects in a generalized algebraic geometry. Versions of a tropical geometry, of an absolute geometry over a field of one element and an algebraic analogue of Arakelov's geometry were realized in this setup.
Another formal generalization is possible to Universal algebraic geometry
Universal algebraic geometry
In universal algebraic geometry, algebraic geometry is generalized from the geometry of rings to geometry of arbitrary varieties of algebras, so that every variety of algebra has its own algebraic geometry. Note that the two terms algebraic variety and variety of algebra should not be...
in which every variety of algebra
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
has its own algebraic geometry. The term variety of algebra should not be confused with algebraic variety.
The language of schemes, stacks and generalizations has proved to be a valuable way of dealing with geometric concepts and became cornerstones of modern algebraic geometry.
Algebraic stacks can be further generalized and for many practical questions like deformation theory and intersection theory, this is often the most natural approach. One can extend the Grothendieck site of affine schemes to a higher categorical
Higher category theory
Higher category theory is the part of category theory at a higher order, which means that some equalities are replaced by explicit arrows in order to be able to explicitly study the structure behind those equalities.- Strict higher categories :...
site of derived affine schemes, by replacing the commutative rings with an infinity category of differential graded commutative algebras, or of simplicial commutative rings or a similar category with an appropriate variant of a Grothendieck topology. One can also replace presheaves of sets by presheaves of simplicial sets (or of infinity groupoids). Then, in presence of an appropriate homotopic machinery one can develop a notion of derived stack as such a presheaf on the infinity category of derived affine schemes, which is satifsying certain infinite categorical version of a sheaf axiom (and to be algebraic, inductively a sequence of representability conditions). Quillen model categories, Segal categories and quasicategories are some of the most often used tools to formalize this yielding the derived algebraic geometry, introduced by the school of Carlos Simpson, including Andre Hirschowitz, Bertrand Toën, Gabrielle Vezzosi, Michel Vaquié and others; and developed further by Jacob Lurie
Jacob Lurie
Jacob Alexander Lurie is an American mathematician, who is currently a professor at Harvard University.-Life:While in school, Lurie took part in the International Mathematical Olympiad, where he won a gold medal with a perfect score in 1994...
, Bertrand Toën, and Gabrielle Vezzosi. Another (noncommutative) version of derived algebraic geometry, using A-infinity categories has been developed from early 1990-s by Maxim Kontsevich
Maxim Kontsevich
Maxim Lvovich Kontsevich is a Russian mathematician. He is a professor at the Institut des Hautes Études Scientifiques and a distinguished professor at the University of Miami...
and followers.
Prehistory: Before the 19th century
Some of the roots of algebraic geometry date back to the work of the Hellenistic GreeksHellenistic Greece
In the context of Ancient Greek art, architecture, and culture, Hellenistic Greece corresponds to the period between the death of Alexander the Great in 323 BC and the annexation of the classical Greek heartlands by Rome in 146 BC...
from the 5th century BC. The Delian problem, for instance, was to construct a length x so that the cube of side x contained the same volume as the rectangular box a2b for given sides a and b. Menechmus (circa 350 BC) considered the problem geometrically by intersecting the pair of plane conics ay = x2 and xy = ab. The later work, in the 3rd century BC, of Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
and Apollonius
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
studied more systematically problems on conic sections, and also involved the use of coordinates. The Arab mathematicians were able to solve by purely algebraic means certain cubic equations, and then to interpret the results geometrically. This was done, for instance, by Ibn al-Haytham in the 10th century AD. Subsequently, Persian
Persian people
The Persian people are part of the Iranian peoples who speak the modern Persian language and closely akin Iranian dialects and languages. The origin of the ethnic Iranian/Persian peoples are traced to the Ancient Iranian peoples, who were part of the ancient Indo-Iranians and themselves part of...
mathematician Omar Khayyám
Omar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
(born 1048 A.D.) discovered the general method of solving cubic equations by intersecting a parabola with a circle. Each of these early developments in algebraic geometry dealt with questions of finding and describing the intersections of algebraic curves.
Such techniques of applying geometrical constructions to algebraic problems were also adopted by a number of Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
mathematicians such as Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
and Niccolò Fontana "Tartaglia"
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...
on their studies of the cubic equation. The geometrical approach to construction problems, rather than the algebraic one, was favored by most 16th and 17th century mathematicians, notably Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
who argued against the use of algebraic and analytical methods in geometry. The French mathematicians Franciscus Vieta and later René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
and Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
revolutionized the conventional way of thinking about construction problems through the introduction of coordinate geometry. They were interested primarily in the properties of algebraic curves, such as those defined by Diophantine equations (in the case of Fermat), and the algebraic reformulation of the classical Greek works on conics and cubics (in the case of Descartes).
During the same period, Blaise Pascal and Gérard Desargues
Gérard Desargues
Girard Desargues was a French mathematician and engineer, who is considered one of the founders of projective geometry. Desargues' theorem, the Desargues graph, and the crater Desargues on the Moon are named in his honour.Born in Lyon, Desargues came from a family devoted to service to the French...
approached geometry from a different perspective, developing the synthetic
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
notions of projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
. Pascal and Desargues also studied curves, but from the purely geometrical point of view: the analog of the Greek ruler and compass construction. Ultimately, the analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
of Descartes and Fermat won out, for it supplied the 18th century mathematicians with concrete quantitative tools needed to study physical problems using the new calculus of Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Leibniz. However, by the end of the 18th century, most of the algebraic character of coordinate geometry was subsumed by the calculus of infinitesimals of Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
and Euler.
Nineteenth and early 20th century
It took the simultaneous 19th century developments of non-Euclidean geometryNon-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
and Abelian integrals in order to bring the old algebraic ideas back into the geometrical fold. The first of these new developments was seized up by Edmond Laguerre
Edmond Laguerre
Edmond Nicolas Laguerre was a French mathematician, a member of the Académie française . His main works were in the areas of geometry and complex analysis. He also investigated orthogonal polynomials...
and Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
, who attempted to ascertain the generalized metric properties of projective space. Cayley introduced the idea of homogeneous polynomial forms, and more specifically quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s, on projective space. Subsequently, Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
studied projective geometry (along with other sorts of geometry) from the viewpoint that the geometry on a space is encoded in a certain class of transformations on the space. By the end of the 19th century, projective geometers were studying more general kinds of transformations on figures in projective space. Rather than the projective linear transformations which were normally regarded as giving the fundamental Kleinian geometry on projective space, they concerned themselves also with the higher degree birational transformations. This weaker notion of congruence would later lead members of the 20th century Italian school of algebraic geometry
Italian school of algebraic geometry
In relation with the history of mathematics, the Italian school of algebraic geometry refers to the work over half a century or more done internationally in birational geometry, particularly on algebraic surfaces. There were in the region of 30 to 40 leading mathematicians who made major...
to classify algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
s up to birational isomorphism.
The second early 19th century development, that of Abelian integrals, would lead Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
to the development of Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s.
Twentieth century
B. L. van der Waerden, Oscar ZariskiOscar Zariski
Oscar Zariski was a Russian mathematician and one of the most influential algebraic geometers of the 20th century.-Education:...
, André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
and others attempted to develop a rigorous foundation for algebraic geometry based on contemporary commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, including valuation theory and the theory of ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
.
In the 1950s and 1960s Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
and Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
recast the foundations making use of sheaf theory. Later, from about 1960, and largely spearheaded by Grothendieck, the idea of schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
was worked out, in conjunction with a very refined apparatus of homological techniques
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
. After a decade of rapid development the field stabilized in the 1970s, and new applications were made, both to number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and to more classical geometric questions on algebraic varieties, singularities
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
and moduli
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
.
An important class of varieties, not easily understood directly from their defining equations, are the abelian varieties
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
, which are the projective varieties whose points form an abelian group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. The prototypical examples are the elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s, which have a rich theory. They were instrumental in the proof of Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
and are also used in elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
.
While much of algebraic geometry is concerned with abstract and general statements about varieties, methods for effective computation with concretely-given polynomials have also been developed. The most important is the technique of Gröbner bases
Gröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
which is employed in all computer algebra systems. Based on these methods, several solvers may compute all the solutions of a system of polynomial equations
Systems of polynomial equations
A system of polynomial equations is a set of simultaneous equations f1 = 0, ..., fh = 0 where the fi are polynomials in several variables, say x1, ..., xn, over some field k....
whose associated variety has dimension zero and thus consists in a finite number of points.
Applications
Algebraic geometry now finds application in statisticsAlgebraic statistics
Algebraic statistics is the use of algebra to advance statistics. Algebra has been useful for experimental design, parameter estimation, and hypothesis testing....
, control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
, error-correcting codes, phylogenetics
Computational phylogenetics
Computational phylogenetics is the application of computational algorithms, methods and programs to phylogenetic analyses. The goal is to assemble a phylogenetic tree representing a hypothesis about the evolutionary ancestry of a set of genes, species, or other taxa...
and geometric modelling. There are also connections to string theory
Homological mirror symmetry
Homological mirror symmetry is a mathematical conjecture made by Maxim Kontsevich. It seeks a systematic mathematical explanation for a phenomenon called mirror symmetry first observed by physicists studying string theory.-History:...
, game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, graph matchings, soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s and integer programming
Integer programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...
. Google Scholar lists hundreds of more studies on algebraic geometry in biology, chemistry, economics, physics and of course other areas of mathematics.
See also
- Algebraic statisticsAlgebraic statisticsAlgebraic statistics is the use of algebra to advance statistics. Algebra has been useful for experimental design, parameter estimation, and hypothesis testing....
- Differential geometry
- Geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
- Intersection theory
- Important publications in algebraic geometry
- List of algebraic surfaces
- Noncommutative algebraic geometryNoncommutative algebraic geometryNoncommutative algebraic geometry is a branch of mathematics, and more specifically a direction in noncommutative geometry that studies the geometric properties of formal duals of non-commutative algebraic objects such as rings as well as geometric objects derived from them...
- Differential algebraic geometryDifferential algebraic geometryDifferential algebraic geometry is an area of differential algebra that adapts concepts and methods from algebraic geometry and applies them to systems of differential equations/algebraic differential equations....
- Real algebraic geometryReal algebraic geometryIn mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....

