
Affine space
Encyclopedia
In mathematics
, an affine space is a geometric structure that generalizes the affine
properties of Euclidean space
. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point that serves as an origin. The solution set of an inhomogeneous linear equation is either empty or an affine space.
may be easier to understand than the usual formal definition: an affine space is what is left of a vector space
after you've forgotten which point is the origin (or, in the words of the French mathematician Marcel Berger
, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps"). Imagine that Alice knows that a certain point is the true origin, and Bob believes that another point — call it p — is the origin. Two vectors, a and b, are to be added. Bob draws an arrow from p to a and another arrow from p to b, and completes the parallelogram to find what Bob thinks is a + b, but Alice knows that it is actually
Similarly, Alice and Bob may evaluate any linear combination
of a and b, or of any finite set of vectors, and will generally get different answers. However, if the sum of the coefficients in a linear combination is 1, then Alice and Bob will arrive at the same answer.
If Alice travels to
then Bob can similarly travel to
Then, for all coefficients λ + (1 − λ) = 1, Alice and Bob describe the same point with the same linear combination, starting from different origins.
Here is the punch line: Alice knows the "linear structure", but both Alice and Bob know the "affine structure"—i.e. the values of affine combinations, defined as linear combinations in which the sum of the coefficients is 1. An underlying set with an affine structure is an affine space.
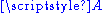 together with a group action
together with a group action
of a vector space
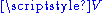 , considered as an Abelian
, considered as an Abelian
Lie group
acting on the left such that the only vector acting with a fixpoint is and there is a single orbit (i.e., the action is free and transitive). It is an example of (left)
and there is a single orbit (i.e., the action is free and transitive). It is an example of (left) 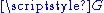 -set, where
-set, where 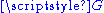 is the additive group
is the additive group 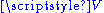 .
.
Explicitly, an affine space is a point set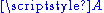 together with a map
together with a map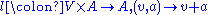
with the following properties:
The vector space
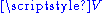 is said to underlie the affine space
is said to underlie the affine space 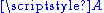 and is also called the difference space.
and is also called the difference space.
By choosing an origin, , one can thus identify
, one can thus identify 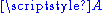 with
with 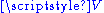 , hence turn
, hence turn 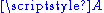 into a vector space. Conversely, any vector space,
into a vector space. Conversely, any vector space, 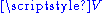 , is an affine space over itself. The uniqueness property ensures that subtraction of any two elements of
, is an affine space over itself. The uniqueness property ensures that subtraction of any two elements of 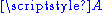 is well defined, producing a vector of
is well defined, producing a vector of 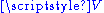 .
.
If ,
,  , and
, and  are points in
are points in 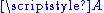 and
and  is a scalar, then
is a scalar, then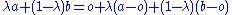
is independent of . Instead of arbitrary linear combinations, only such affine combinations of points have meaning.
. Instead of arbitrary linear combinations, only such affine combinations of points have meaning.
By noting that one can define subtraction of points of an affine space as follows: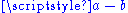 is the unique vector in
is the unique vector in 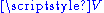 such that
such that 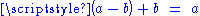 ,
,
one can equivalently define an affine space as a point set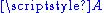 , together with a vector space
, together with a vector space 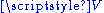 , and a subtraction map
, and a subtraction map 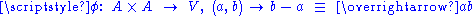 with the following properties :
with the following properties :
These two properties are called Weyl's axioms.
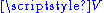 is a subset closed under affine combinations of vectors in the space. For example, the set
is a subset closed under affine combinations of vectors in the space. For example, the set

is an affine space, where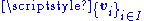 is a family of vectors in
is a family of vectors in 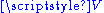 – this space is the affine span of these points. To see that this is indeed an affine space, observe that this set carries a transitive action of the vector subspace
– this space is the affine span of these points. To see that this is indeed an affine space, observe that this set carries a transitive action of the vector subspace 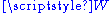 of
of 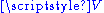

This affine subspace can be equivalently described as the coset of the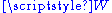 -action
-action
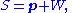
where is any element of
is any element of 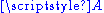 , or equivalently as any level set
, or equivalently as any level set
of the quotient map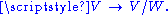 A choice of
A choice of  gives a base point of
gives a base point of 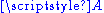 and an identification of
and an identification of 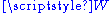 with
with 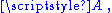 but there is no natural choice, nor a natural identification of
but there is no natural choice, nor a natural identification of 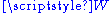 with
with 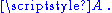
A linear transformation is a function that preserves all linear combination
s; an affine transformation is a function that preserves all affine combinations. A linear subspace is an affine subspace containing the origin, or, equivalently, a subspace that is closed under linear combinations.
For example, in , the origin, lines and planes through the origin and the whole space are linear subspaces, while points, lines and planes in general as well as the whole space are the affine subspaces.
, the origin, lines and planes through the origin and the whole space are linear subspaces, while points, lines and planes in general as well as the whole space are the affine subspaces.
are linearly dependent if there exist scalars a1, a2, …,an, not all zero, for which
Similarly they are affinely dependent if the same is true and also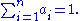
Equation is an affine relation among the vectors v1, v2, …, vn.
using coordinates, or equivalently vector spaces. It can also be studied as synthetic geometry
by writing down axioms, though this approach is much less common. There are several different systems of axioms for affine space.
axiomatizes affine geometry (over the reals) as ordered geometry
together with an affine form of Desargues's theorem and an axiom stating that in a plane there is at most one line through a given point not meeting a given line.
Affine planes satisfy the following axioms :
(in which two lines are called parallel if they are equal or
disjoint):
As well as affine planes over fields (or division ring
s), there are also many non-Desarguesian plane
s satisfying these axioms. gives axioms for higher dimensional affine spaces.
s of projective space
s: an affine plane can be obtained from any projective plane
by removing a line and all the points on it, and conversely any affine plane can be used to construct a projective plane as a closure
by adding a "line at infinity" whose points correspond to equivalence classes of parallel lines.
Further, transformations of projective space that preserve affine space (equivalently, that preserve the points at infinity as a set) yield transformations of affine space, and conversely any affine linear transformation extends uniquely to a projective linear transformations, so affine transformations are a subset of projective transforms. Most familiar is that Möbius transformations (transformations of the projective line, or Riemann sphere) are affine (transformations of the complex plane) if and only if they fix the point at infinity.
However, one cannot take the projectivization of an affine space, so projective spaces are not naturally quotient
s of affine spaces: one can only take the projectivization of a vector space, since the projective space is lines through a given point, and there is no distinguished point in an affine space. If one chooses a base point (as zero), then an affine space becomes a vector space, which one may then projectivize, but this requires a choice.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an affine space is a geometric structure that generalizes the affine
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
properties of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point that serves as an origin. The solution set of an inhomogeneous linear equation is either empty or an affine space.
Informal descriptions
The following characterizationCharacterization (mathematics)
In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
may be easier to understand than the usual formal definition: an affine space is what is left of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
after you've forgotten which point is the origin (or, in the words of the French mathematician Marcel Berger
Marcel Berger
Marcel Berger is a French mathematician, doyen of French differential geometry, and a former director of the Institut des Hautes Études Scientifiques , France...
, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps"). Imagine that Alice knows that a certain point is the true origin, and Bob believes that another point — call it p — is the origin. Two vectors, a and b, are to be added. Bob draws an arrow from p to a and another arrow from p to b, and completes the parallelogram to find what Bob thinks is a + b, but Alice knows that it is actually
- p + (a − p) + (b − p).
Similarly, Alice and Bob may evaluate any linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of a and b, or of any finite set of vectors, and will generally get different answers. However, if the sum of the coefficients in a linear combination is 1, then Alice and Bob will arrive at the same answer.
If Alice travels to
- λa + (1 − λ)b
then Bob can similarly travel to
- p + λ(a − p) + (1 − λ)(b − p) = λa + (1 − λ)b.
Then, for all coefficients λ + (1 − λ) = 1, Alice and Bob describe the same point with the same linear combination, starting from different origins.
Here is the punch line: Alice knows the "linear structure", but both Alice and Bob know the "affine structure"—i.e. the values of affine combinations, defined as linear combinations in which the sum of the coefficients is 1. An underlying set with an affine structure is an affine space.
Definition
An affine space is a set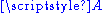 together with a group action
together with a group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
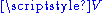 , considered as an Abelian
, considered as an AbelianAbelian
In mathematics, Abelian refers to any of number of different mathematical concepts named after Niels Henrik Abel:- Group theory :*Abelian group, a group in which the binary operation is commutative...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
acting on the left such that the only vector acting with a fixpoint is
 and there is a single orbit (i.e., the action is free and transitive). It is an example of (left)
and there is a single orbit (i.e., the action is free and transitive). It is an example of (left) 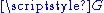 -set, where
-set, where 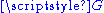 is the additive group
is the additive group 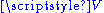 .
.Explicitly, an affine space is a point set
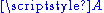 together with a map
together with a map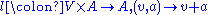
with the following properties:
- Left identity
-
- Associativity
-
- Uniqueness
-
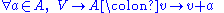 is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
.
-
The vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
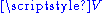 is said to underlie the affine space
is said to underlie the affine space 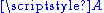 and is also called the difference space.
and is also called the difference space.By choosing an origin,
 , one can thus identify
, one can thus identify 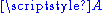 with
with 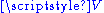 , hence turn
, hence turn 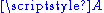 into a vector space. Conversely, any vector space,
into a vector space. Conversely, any vector space, 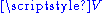 , is an affine space over itself. The uniqueness property ensures that subtraction of any two elements of
, is an affine space over itself. The uniqueness property ensures that subtraction of any two elements of 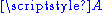 is well defined, producing a vector of
is well defined, producing a vector of 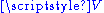 .
.If
 ,
,  , and
, and  are points in
are points in 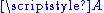 and
and  is a scalar, then
is a scalar, then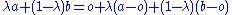
is independent of
 . Instead of arbitrary linear combinations, only such affine combinations of points have meaning.
. Instead of arbitrary linear combinations, only such affine combinations of points have meaning.By noting that one can define subtraction of points of an affine space as follows:
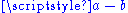 is the unique vector in
is the unique vector in 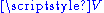 such that
such that 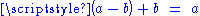 ,
,one can equivalently define an affine space as a point set
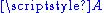 , together with a vector space
, together with a vector space 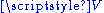 , and a subtraction map
, and a subtraction map 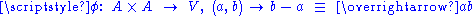 with the following properties :
with the following properties :
-
 there is a unique point
there is a unique point 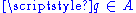 such that
such that 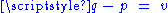 and
and -
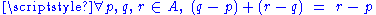 .
.
These two properties are called Weyl's axioms.
Examples
- When children find the answers to sums such as 4+3 or 4−2 by counting right or left on a number lineNumber lineIn basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...
, they are treating the number line as a one-dimensional affine space. - Any cosetCosetIn mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of a subspace of a vector space is an affine space over
of a vector space is an affine space over 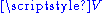 .
. - If
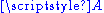 is a matrix and
is a matrix and  lies in its column space, the set of solutions of the equation
lies in its column space, the set of solutions of the equation  is an affine space over the subspace of solutions of
is an affine space over the subspace of solutions of  .
. - The solutions of an inhomogeneous linear differential equation form an affine space over the solutions of the corresponding homogeneous linear equation.
- Generalizing all of the above, if
 is a linear mapping and y lies in its image, the set of solutions
is a linear mapping and y lies in its image, the set of solutions 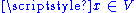 to the equation
to the equation  is a coset of the kernel of
is a coset of the kernel of 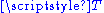 , and is therefore an affine space over
, and is therefore an affine space over  .
.
Affine subspaces
An affine subspace (sometimes called a linear manifold, linear variety, or a flat) of a vector space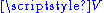 is a subset closed under affine combinations of vectors in the space. For example, the set
is a subset closed under affine combinations of vectors in the space. For example, the set
is an affine space, where
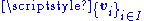 is a family of vectors in
is a family of vectors in 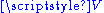 – this space is the affine span of these points. To see that this is indeed an affine space, observe that this set carries a transitive action of the vector subspace
– this space is the affine span of these points. To see that this is indeed an affine space, observe that this set carries a transitive action of the vector subspace 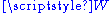 of
of 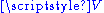

This affine subspace can be equivalently described as the coset of the
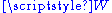 -action
-action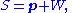
where
 is any element of
is any element of 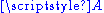 , or equivalently as any level set
, or equivalently as any level setLevel set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
of the quotient map
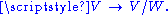 A choice of
A choice of  gives a base point of
gives a base point of 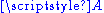 and an identification of
and an identification of 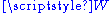 with
with 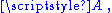 but there is no natural choice, nor a natural identification of
but there is no natural choice, nor a natural identification of 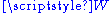 with
with 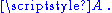
A linear transformation is a function that preserves all linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s; an affine transformation is a function that preserves all affine combinations. A linear subspace is an affine subspace containing the origin, or, equivalently, a subspace that is closed under linear combinations.
For example, in
 , the origin, lines and planes through the origin and the whole space are linear subspaces, while points, lines and planes in general as well as the whole space are the affine subspaces.
, the origin, lines and planes through the origin and the whole space are linear subspaces, while points, lines and planes in general as well as the whole space are the affine subspaces.Affine combinations and affine dependence
An affine combination is a linear combination in which the sum of the coefficients is 1. Just as members of a set of vectors are linearly independent if none is a linear combination of the others, so also they are affinely independent if none is an affine combination of the others. The set of linear combinations of a set of vectors is their "linear span" and is always a linear subspace; the set of all affine combinations is their "affine span" and is always an affine subspace. For example, the affine span of a set of two points is the line that contains both; the affine span of a set of three non-collinear points is the plane that contains all three. Vectors- v1, v2, ..., vn
are linearly dependent if there exist scalars a1, a2, …,an, not all zero, for which
Similarly they are affinely dependent if the same is true and also
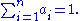
Equation is an affine relation among the vectors v1, v2, …, vn.
Axioms
Affine space is usually studied as analytic geometryAnalytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
using coordinates, or equivalently vector spaces. It can also be studied as synthetic geometry
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
by writing down axioms, though this approach is much less common. There are several different systems of axioms for affine space.
axiomatizes affine geometry (over the reals) as ordered geometry
Ordered geometry
Ordered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement...
together with an affine form of Desargues's theorem and an axiom stating that in a plane there is at most one line through a given point not meeting a given line.
Affine planes satisfy the following axioms :
(in which two lines are called parallel if they are equal or
disjoint):
- Any two distinct points lie on a unique line.
- Given a point and line there is a unique line which contains the point and is parallel to the line
- There exist three non-collinear points.
As well as affine planes over fields (or division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s), there are also many non-Desarguesian plane
Non-Desarguesian plane
In mathematics, a non-Desarguesian plane, named after Gérard Desargues, is a projective plane that does not satisfy Desargues's theorem, or in other words a plane that is not a Desarguesian plane...
s satisfying these axioms. gives axioms for higher dimensional affine spaces.
Relation to projective spaces
Affine spaces are subspaceSubspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
s of projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s: an affine plane can be obtained from any projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
by removing a line and all the points on it, and conversely any affine plane can be used to construct a projective plane as a closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
by adding a "line at infinity" whose points correspond to equivalence classes of parallel lines.
Further, transformations of projective space that preserve affine space (equivalently, that preserve the points at infinity as a set) yield transformations of affine space, and conversely any affine linear transformation extends uniquely to a projective linear transformations, so affine transformations are a subset of projective transforms. Most familiar is that Möbius transformations (transformations of the projective line, or Riemann sphere) are affine (transformations of the complex plane) if and only if they fix the point at infinity.
However, one cannot take the projectivization of an affine space, so projective spaces are not naturally quotient
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
s of affine spaces: one can only take the projectivization of a vector space, since the projective space is lines through a given point, and there is no distinguished point in an affine space. If one chooses a base point (as zero), then an affine space becomes a vector space, which one may then projectivize, but this requires a choice.
See also
- affine geometryAffine geometryIn mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
- affine transformationAffine transformationIn geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
- affine groupAffine groupIn mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
- equipollence (geometry)Equipollence (geometry)In geometry, equipollence is a certain relationship between ordered pairs of points. A pair of points and another pair are equipollent precisely if the distance and direction from a to b are respectively the same as the distance and direction from c to d.- In affine spaces over a field...
- interval measurement, an affine observable in statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
- heap (mathematics)Heap (mathematics)In abstract algebra, a heap is a mathematical generalisation of a group. Informally speaking, a heap is obtained from a group by "forgetting" which element is the unit, in the same way that an affine space can be viewed as a vector space in which the 0 element has been "forgotten"...
- Space (mathematics)



